ก่อนหน้านี้ได้เขียนบทความเรื่องการวิเคราะห์จำแนกประเภทข้อมูลเป็นสองกลุ่มด้วยการถดถอยโลจิสติกไป https://phyblas.hinaboshi.com/20161103

ตอนท้ายได้กล่าวถึงว่าการวิเคราะห์ในลักษณะนี้สามารถพัฒนาต่อไปสู่การจำแนกประเภทกลุ่มของข้อมูลเป็นมากกว่าสองได้ด้วย และนั่นคือสิ่งที่จะเขียนถึงในคราวนี้

ขอเริ่มจากยกตัวอย่างปัญหาที่ต้องการจะแก้ขึ้นมา

สมมุติว่ามีเกมอยู่เกมหนึ่งซึ่งภายในเกมมีการเลี้ยงพญานาค โดยต้องเลี้ยงตั้งแต่เด็กแล้วพอถึงอายุถึงกำหนดก็จะเปลี่ยนร่างเป็นร่างสมบูรณ์

พญานาคร่างสมบูรณ์ไม่ได้มีเพียงรูปแบบเดียว แต่จะต่างกันออกไปขึ้นอยู่กับว่าตอนเด็กอยู่ให้อาหารอะไรไปแค่ไหน

สมมุติว่าอาหารพญานาคในเกมนี้มีแค่ ๒ อย่างคือผักและปลา มีผู้เล่นคนหนึ่งลองเลี้ยงซ้ำทั้งหมดร้อยครั้งแล้วให้อาหารปริมาณต่างกันออกไป ผลที่ได้ออกมาตามนี้



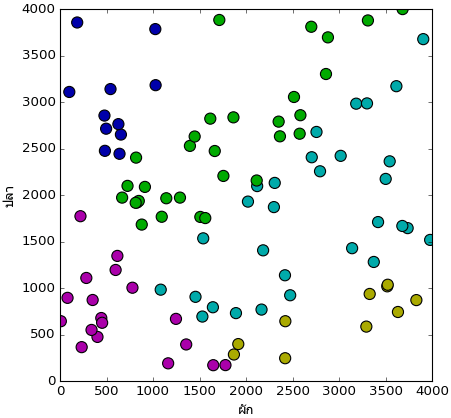
จากภาพนี้ผลที่ได้จำแนกตามพื้นที่ออกเป็น ๕ ส่วน ดังนี้
0. สีม่วง ไม่เปลี่ยนร่าง
1. สีเหลือง พญานาคเหลือง
2. สีฟ้า พญานาคฟ้า
3. สีเขียว พญานาคเขียว
4. สีน้ำเงิน พญานาคน้ำเงิน

แค่มองจากตรงนี้ก็คงพอเห็นภาพคร่าวๆแล้วว่ามีกฎเกณฑ์การจำแนกเป็นยังไง

ความจริงแล้วข้อมูลชุดนี้ถูกสร้างขึ้นมาด้วยโค้ดนี้
หมายเลขที่อยู่ในตัวแปร plianrang แสดงถึงว่าจะเปลี่ยนเป็นร่างไหน ตามเลขที่เขียนไว้ข้างต้น
ได้

ดูโค้ดตรงนี้แล้วเราคงเข้าในกฎเกณฑ์การจำแนกเป็นอย่างดี อย่างไรก็ตาม จากตรงนี้จะลืมโค้ดข้างต้นนี้ไปให้หมด แล้วตั้งคำถามว่าจะขีดเส้นแบ่งพื้นที่อย่างไรดีโดยดูจากผลที่ได้ในรูปนี้ หากมีการเลี้ยงพญานาคตัวใหม่อีกครั้งเราจะทำนายได้ว่าจะได้ร่างอะไรโดยดูจากปริมาณอาหารที่ให้

เราจะเขียนโปรแกรมให้เครื่องทำการเรียนรู้ที่จะลากเส้นแบ่งเองโดยที่มันไม่รู้ที่มาของข้อมูล ไม่รู้ว่าเราใช้สูตรอะไรจึงได้อย่างนี้มา ข้อมูลที่เราจะป้อนให้มีแค่ค่าตัวแปรต้นและผลที่ได้เท่านั้น



โจทย์ครั้งนี้ใกล้เคียงกับเรื่องการปลูกถั่วที่ยกไปแล้ว เป็นปัญหาสองมิติ (มีตัวแปรต้น ๒ ตัว) เหมือนกัน ต่างกันตรงที่ว่าถั่วเราสนใจแค่ว่างอกหรือไม่งอก มีแค่ ๒ คำตอบ แต่พญานาคเราสนใจว่ามันจะกลายเป็นร่างอะไร มีมากถึง ๕ คำตอบ

การวิเคราะห์การถดถอยโลจิสติกสำหรับการจำแนกประเภทข้อมูลเป็นหลายกลุ่มนั้นเรียกว่าการถดถอยโลจิสติกแบบมัลติโนเมียล (multinomial logistic regression) และบางครั้งก็ถูกเรียกว่าการถดถอยซอฟต์แม็กซ์ (softmax regression) ในที่นี้ก็จะเรียกแบบนั้นเพื่อแยกให้ชัด

ในการวิเคราะห์การถอถอยซอฟต์แม็กซ์จะใช้ฟังก์ชันที่เรียกว่าซอฟต์แม็กซ์ (softmax) เพื่อหาความน่าจะเป็นที่จะอยู่ในกลุ่มใดๆ ซึ่งต่างจากการวิเคราะห์การถดถอยโลจิสติกที่ใช้ฟังก์ชันซิกมอยด์

ในตอนที่จำแนกข้อมูลเป็นสองกลุ่มนั้นในขั้นตอนก่อนสุดท้ายซึ่งหาความน่าจะเป็นนั้นเราใช้ฟังก์ชันซิกมอยด์ ผลที่ได้คือค่าความน่าจะเป็นที่ข้อมูลอันหนึ่งๆจะอยู่ในกลุ่มหนึ่ง ค่าที่ได้อยู่ระหว่าง 0 ถึง 1 และความน่าจะเป็นที่จะอยู่อีกกลุ่มก็เอาค่าที่ได้นี้ไปหักออกจาก 1 อีกที เพราะรวมแล้วต้องเท่ากับ 1

แต่พอมีการจำแนกมากกว่าสองกลุ่มจะใช้วิธีแบบนั้นไม่ได้แล้ว เพราะถึงคำนวณความน่าจะเป็นที่จะถูกจัดอยู่ในกลุ่มหนึ่งได้แล้วหักออกจาก 1 ไปก็ไม่รู้ว่าความน่าจะเป็นที่เหลืออยู่นั้นเป็นของกลุ่มไหนในกลุ่มที่เหลือ

ดังนั้นจึงจำเป็นจะต้องหาความน่าจะเป็นของทุกกลุ่มพร้อมๆกันแล้วนำมาคำนวณเปรียบเทียบอีกที

เพื่อให้เห็นภาพชัดลองเขียนเป็นแผนภาพดู ขอยกตัวอย่างกรณีที่มีตัวแปรต้น ๒ ตัว เช่นในโจทย์ข้อนี้ x คือจำนวนผักและ y คือจำนวนปลา

 

ถ้าเป็นสำหรับกรณีการถดถอยโลจิสติกแบบเดิมจะเขียนได้แบบนี้



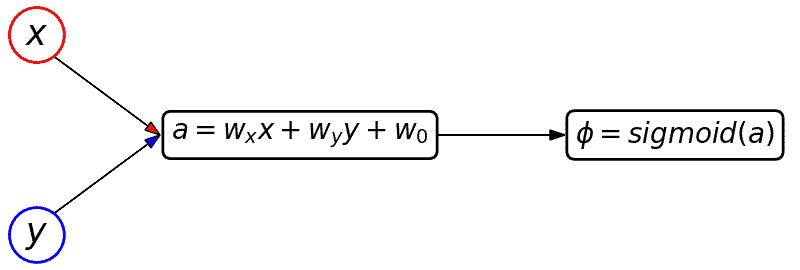
ส่วนกรณีการถดถอยซอฟต์แม็กซ์จะเป็นแบบนี้



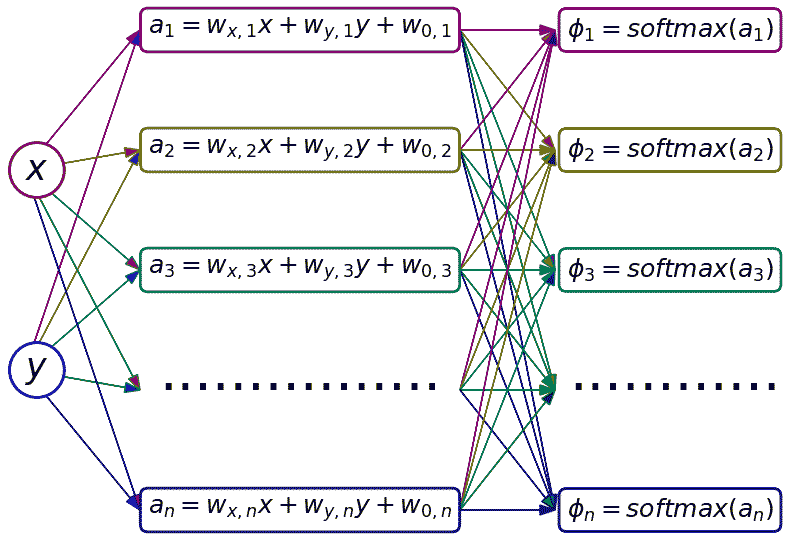
จะเห็นว่าจำนวนข้อมูลที่ต้องคำนวณเพิ่มเป็นจำนวน n ตามจำนวนกลุ่มที่จะจำแนก และฟังก์ชันสำหรับคำนวณความน่าจะเป็นในท้ายสุดที่เข้ามาแทนที่ฟังก์ชันซิกมอยด์ก็คือฟังก์ชันซอฟต์แม็กซ์

ฟังก์ชันซอฟต์แม็กซ์นิยามดังนี้
$\begin{align} \textbf{softmax}(a_k) = \frac{e^{a_k}}{\sum_l e^{a_l}} \end{align}$ ...


โดยที่ n เป็นจำนวนกลุ่มประเภทของข้อมูลที่ต้องการจะจำแนก

เทียบกับซิกมอยด์แล้วจะดูคล้ายกันมาก ที่จริงแล้วซอฟต์แม็กซ์คือซิกมอยด์ที่ทำให้เป็นรูปทั่วไปมากขึ้น และสามารถเห็นได้ว่าถ้าจำนวนกลุ่มมีแค่สองฟังก์ชันซอฟต์แม็กซ์จะเกือบเหมือนกับซิกมอยด์

และจากทั้งสมการจะเห็นได้ว่าการคำนวณซอฟต์แม็กซ์ต้องใช้ค่า a ที่ได้จากการคำนวณทุกกลุ่ม ดังนั้นลูกศรในภาพจึงระโยงระยางลากเชื่อมทุกตัว

การเขียนฟังก์ชันซอฟต์แม็กซ์ขึ้นมาในไพธอนนั้นมีความซับซ้อนเล็กน้อย จึงขอแยกไปอธิบายในหน้าอื่น สำหรับผู้ที่สนใจตามอ่านได้ที่ https://phyblas.hinaboshi.com/20161206

ผลลัพธ์ที่ได้จากซอฟต์แม็กซ์จะได้ออกมาจำนวนเท่ากับจำนวนกลุ่ม โดยเป็นค่าความน่าจะเป็นที่จะอยู่ในกลุ่มนั้นๆ ซึ่งถ้าเอามารวมกันทั้งหมดจะได้เป็น 1 เสมอ

ในขณะที่ผลลัพธ์จริงๆที่เราป้อนเข้าไปเพื่อให้โปรแกรมเรียนรู้นั้นคือสิ่งที่เรารู้แน่ชัดอยู่แล้วว่าอยู่กลุ่มไหน ดังนั้นจะอยู่ในรูปที่มีอยู่อันเดียวที่เป็น 1 อันที่เหลือเป็น 0 ลักษณะข้อมูลแบบนี้เรียกว่าวันฮ็อต (one-hot)

เช่นผลอาจทำนายว่าความน่าจะเป็นของแต่ละกลุ่มคือ 0.05,0.9,0.01,0.005,0.035

ในขณะที่ผลจริงๆอาจเป็น 0,1,0,0,0 เป็นต้น

สำหรับในตัวอย่างที่เรายกขึ้นมาข้างต้นนั้นผลการเปลี่ยนร่างที่ถูกเก็บอยู่ในตัวแปร plianrang นั้นอยู่ในรูปตัวเลข 0 ถึง 4 ข้อมูลตรงนี้ยังใช้ไม่ได้ทันทีจำเป็นต้องทำการแปลงให้อยู่ในรูปดังที่ว่าก่อน

การแปลงสามารถทำได้โดยเขียนแบบนี้

ผลที่ได้คือถ้าค่าใน plianrang เป็นเลขไหน ค่าใน plianrang_1h ก็จำเป็น 1 ในตำแหน่งนั้น และที่เหลือเป็น 0
ในที่นี้โค้ดอาจดูเข้าใจยากสักหน่อย ในนี้ [:,None] เป็นการเปลี่ยนอาเรย์จากหนึ่งมิติให้เป็นสองมิติ หรือจะเขียนเป็น .reshape(1,-1) ก็ได้เช่นกัน

ในขณะที่ range(5) จะเป็นอาเรย์หนึ่งมิติ เมื่อนำมาเข้าคู่คำนวณกันจะเป็นการแจกแจง ผลที่ได้คือเป็นอาเรย์ที่มีรูปร่างเป็นจำนวนข้อมูลคูณด้วย 5

และ +0 ที่เติมเข้าไปนี้แค่เพื่อเปลี่ยนให้ค่าเป็นชนิดจำนวนเต็มเท่านั้น เพราะที่ได้จากการคำนวณทางตรรกะจะเป็นชนิดบูล (True False) ที่จริงจะใช้ .astype(int) แทนก็ได้ แต่เขียนแบบนี้สั้นกว่ามาก

แต่ที่จริงจะไม่เปลี่ยนเป็น int ก็ได้ ปล่อยให้เป็น True False ไปทั้งอย่างนั้นก็นำมาใช้ในการคำนวณได้เช่นกัน โดย True=1 False=0 ดังนั้นในตัวอย่างโค้ดที่จะเขียนจะใช้ทั้งๆแบบนั้น ไม่ใส่ +0



อีกเรื่องที่จะต้องมาคิดก็คือเรื่องค่าน้ำหนักและไบแอสของแบบจำลอง

ถ้าเป็นการถดถอยโลจิสแบบเดิมสมการที่ใช้คำนวณคือ wx+wy+w0 นั่นคือมีค่าน้ำหนักแค่ ๒ ตัวคือ wx และ wy และไบแอสคือ w0

แต่กรณีถดถอยซอฟต์แม็กซ์เราต้องคิดแยกกันเป็นหลายอัน ดังนั้นจึงมี wx, wy และ w0 อย่างละหลายอัน

นั่นคือจะเป็น wx[0], wx[1], ... กับ wy[0], wy[1], ... แล้วก็ w0[0], w0[1], ...

และเวลาที่คำนวณก็จะเป็น wx[n]*x[:,n]+wy[n]*y[:,n]+w0[n] แบบนี้ เป็นต้น

ดูแล้วยุ่งยากขึ้นมากทีเดียว และที่จะยุ่งยากขึ้นไปอีกคือเรื่องการหาค่าความชันของฟังก์ชันเพื่อที่จะคำนวณการเปลี่ยนแปลงค่าน้ำหนักและไบแอส

ลองไล่คิดดูทีละขั้น เริ่มจากฟังก์ชันค่าเสียหาย ในที่นี้ใช้เป็นผลรวมความคลาดเคลื่อนกำลังสองเช่นเดียวกับที่ใช้ในการถดถอยโลจิสติก แต่เมื่อมีค่าของหลายกลุ่มดังนั้นจึงต้องรวมทุกกลุ่ม เขียนสมการก็จะได้แบบนี้
$\begin{align} J = \sum_i\sum_k \left( z_{k,(i)}-\phi_{k,(i)} \right) \end{align}$ ..(1)

ในที่นี้ i คือดัชนีของแถวข้อมูล ส่วน k คือดัชนีของกลุ่ม

z คือคำตอบจริงซึ่งอยู่ในรูปของ one-hot

ส่วน φ สำหรับในที่นี้คือค่าที่คำนวณจากฟังก์ชันซอฟต์แม็กซ์
$\begin{align} \phi_{k,(i)} = \frac{e^{a_{k,(i)}}}{\sum_l e^{a_{l,(i)}}} \end{align}$ ..(2)

โดย H คือผลรวมของตัวแปรต้นคูณน้ำหนักในแต่ละมิติ
$\begin{align} a_{m,(i)} = \sum_{j}w_{j,m}x_{j,(i)} = w_{x,m}x_{(i)}+w_{y,m}y_{(i)} +w_{0,m} \end{align}$ ..(3)

โดย w_j คือค่าน้ำหนักในมิติต่างๆ ในที่นี้เป็นสองมิติจะมี ๓ ตัวคือ wx wy และ w0 และแต่ละตัวยังมี m ห้อยต่อท้าย m ในที่นี้เป็นดัชนีแสดงถึงกลุ่ม เช่นเดียวกับ k

เราต้องการค่าความเปลี่ยนแปลงของค่าเสียหายเทียบกับน้ำหนักต่าง ซึ่งสามารถคำนวณได้จากกฎลูกโซ่ นั่นคือ
$\begin{align} \frac{\partial J}{\partial w_{j,m}} = \sum_i \sum_k \frac{\partial J}{\partial \phi_{k,(i)}} \frac{\partial \phi_{k,(i)}}{\partial a_{m,(i)}} \frac{\partial a_{m,(i)}}{\partial w_{j,m}} \end{align}$ ..(4)

ก้อนแรกคือจากสมการ (1) มาหาอนุพันธ์ของค่าเสียหายเทียบกับ φ ได้
$\begin{align} \frac{\partial J}{\partial \phi_{k,(i)}} = 2(\phi_{k,(i)}-z_{k,(i)}) \end{align}$ ..(5)

ก้อนต่อมาคือจากสมการ (2) หาอนุพันธ์ของ φ เทียบกับ a ได้
$\begin{align} \frac{\partial \phi_{k,(i)}}{\partial a_{m,(i)}} = \phi_{k,(i)}(\delta_{k,m}-\phi_{m,(i)}) \end{align}$ ..(6)

ในที่นี้ δ คือเดลตาของโครเน็กเกอร์ จะเป็น 1 เมื่อ k=m และเป็น 0 เมื่อ k≠m

ก้อนสุดท้ายได้จากสมการ (3) หาอนุพันธ์ของ a เทียบกับ x_j ได้
$\begin{align} \frac{\partial a_{m,(i)}}{\partial w_{j,m}} = x_{j,(i)} \end{align}$ ..(7)

หรือถ้าแทน x_j ด้วย x, y และ wj ด้วย wx, wy, w0 จะได้
$\begin{align} \frac{\partial a_{m,(i)}}{\partial w_{x,m}} &= x_{(i)} \\ \frac{\partial a_{m,(i)}}{\partial w_{y,m}} &= y_{(i)} \\ \frac{\partial a_{m,(i)}}{\partial w_{0,m}} &= 1 \end{align}$ ..(8)

นำ (5)(6)(7) แทนลงใน (4) จะได้
$\begin{align} \frac{\partial a_{m,(i)}}{\partial w_{j,m}} = 2\sum_i\sum_k\phi_{k,(i)}(\delta_{k,m}-\phi_{m,(i)})(\phi_{k,(i)}-z_{k,(i)})x_{j,(i)} \end{align}$ ..(9)

หรือถ้าแทน (5)(6)(8) จะได้
$\begin{align} \frac{\partial a_{m,(i)}}{\partial w_{x,m}} &= 2\sum_i\sum_k\phi_{k,(i)}(\delta_{k,m}-\phi_{m,(i)})(\phi_{k,(i)}-z_{k,(i)})x_{(i)} \\ \frac{\partial a_{m,(i)}}{\partial w_{y,m}} &= 2\sum_i\sum_k\phi_{k,(i)}(\delta_{k,m}-\phi_{m,(i)})(\phi_{k,(i)}-z_{k,(i)})y_{(i)} \\ \frac{\partial a_{m,(i)}}{\partial w_{0,m}} &= 2\sum_i\sum_k\phi_{k,(i)}(\delta_{k,m}-\phi_{m,(i)})(\phi_{k,(i)}-z_{k,(i)}) \end{align}$ ..(10)

สุดท้ายคำนวณค่าน้ำหนักที่ควรจะเปลี่ยนในแต่ละรอบการเรียนรู้ได้โดย
$\begin{align} \Delta w_{j,m} = -\eta\frac{\partial J}{\partial w_{j,m}} \end{align}$ ..(11)

โดย η คืออัตราการเรียนรู้

แทน (9) ลงใน (11)
$\begin{align} \Delta w_{j,m} = 2\eta\sum_i\sum_k\phi_{k,(i)}(\delta_{k,m}-\phi_{m,(i)})(z_{k,(i)}-\phi_{k,(i)})x_{j,(i)} \end{align}$ ..(12)

หรือแทน (10) ลงใน (11) จะได้
$\begin{align} \Delta w_{x,m} &= 2\eta\sum_i\sum_k\phi_{k,(i)}(\delta_{k,m}-\phi_{m,(i)})(z_{k,(i)}-\phi_{k,(i)})x_{(i)} \\ \Delta w_{y,m} &= 2\eta\sum_i\sum_k\phi_{k,(i)}(\delta_{k,m}-\phi_{m,(i)})(z_{k,(i)}-\phi_{k,(i)})y_{(i)} \\ \Delta w_{0,m} &= 2\eta\sum_i\sum_k\phi_{k,(i)}(\delta_{k,m}-\phi_{m,(i)})(z_{k,(i)}-\phi_{k,(i)}) \end{align}$ ..(13)

สมการนี้คือสมการที่เราจะใช้ในโปรแกรมวิเคราะห์การถดถอยซอฟต์แม็กซ์



เมื่อได้สมการมาแล้วต่อมาก็นำมาใช้เขียนโค้ดได้เลย ในที่นี้ก่อนเริ่มเข้าสู่ส่วนการเรียนรู้จะมีการทำข้อมูลให้เป็นมาตรฐาน และมีการปรับค่าน้ำหนักกลับหลังเรียนรู้เสร็จ ดังที่อธิบายไปในนี้ด้วย https://phyblas.hinaboshi.com/20161124

โค้ดตั้งแต่เริ่มโหลดข้อมูลอาหารพญานาคมาแล้วก็ทำการเรียนรู้เพื่อปรับน้ำหนักเสร็จเรียบร้อย
ค่าเสียหายและจำนวนที่ทายถูกที่เปลี่ยนแปลงไประหว่างการเรียนรู้ถูกบันทึกเอาไว้ในตัวแปร khasiahai และ thuktong ลองนำมาวาดกราฟ
จะเห็นว่าการเรียนรู้คืบหน้าไปตามที่ต้องการ ยิ่งผ่านไปยิ่งทายถูกมากขึ้นเรื่อยๆจนเกือบถูกหมด



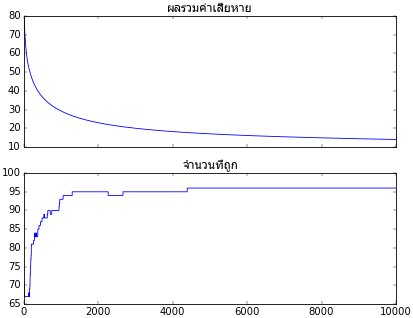
จากนั้นลองวาดภาพแสดงผลการจำแนกประเภทดู โดยสร้างโครงข่ายตามแกน x และ y ขึ้นมาด้วย np.meshgrid จากนั้นทำนายผลว่าในแต่ละจุดบนโครงข่ายนี้ควรจัดอยู่ในกลุ่มไหนโดยใช้ค่าน้ำหนักที่ได้มาจากการเรียนรู้ จากนั้นวาดจุดกระจายทั่วด้วย scatter แล้ววาดเส้นคั่นด้วย contour
ได้ภาพที่มีการแบ่งเขตเป็นสีต่างๆอย่างสวยงาม และมีจุดสีต่างๆซึ่งสอดคล้องกับสีของเขตนั้นๆ สีที่อยู่ผิดเขตจะมีขอบแดงล้อม หมายถึงทายผิด



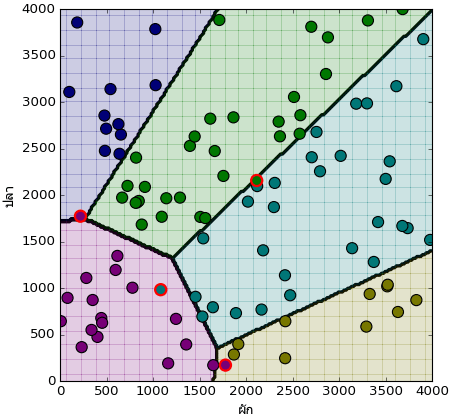
การจำแนกกลุ่มด้วยการถดถอยโลจิสติกนั้นเส้นแบ่งที่ได้จะเป็นเส้นตรงเสมอ เพราะได้จากการคำนวณเชิงเส้น การถดถอยซอฟต์แม็กซ์ก็เช่นกัน แม้จะมีหลายเส้นแบ่งแต่ทั้งหมดก็คือเส้นตรง



เรื่องหนึ่งที่น่าสังเกตก็คือ ฟังก์ชันซอฟต์แม็กซ์ไม่ได้ทำให้ลำดับการจัดเรียงค่าเปลี่ยนไป กล่าวคือตัวไหนมีค่ามากสุดก็ยังมากสุดอยู่ ดังนั้นหากแค่จะใช้ argmax เพื่อหาว่าอันไหนมีค่ามากสุดเพื่อทำนายว่าอยู่กลุ่มไหน กรณีแบบนี้ไม่ต้องผ่านซอฟต์แม็กซ์ ใช้ค่าที่ได้จากผลรวมของผลคูณน้ำหนักกับตัวแปรต้นได้เลย

นั่นคือ thukmai = phi.argmax(1) จะเปลี่ยนเป็น (wx*X[:,0:1]+wy*X[:,1:2]+w0).argmax(1) ก็ไม่ต่างกัน

ฟังก์ชันซอฟต์แม็กซ์ใช้แค่เมื่อต้องการคำนวณค่าเสียหายเพื่อนำมาใช้ในการเรียนรู้เท่านั้น



เมื่อได้ผลตามที่ต้องการสำเร็จแล้วต่อไปเราจะมาปรับปรุงให้ดีขึ้นด้วยการเขียนในรูปของคลาสเพื่อให้เป็นระบบใช้งานง่าย

พร้อมกันนั้นก็ปรับให้สามารถรองรับข้อมูลที่เป็นกี่มิติก็ได้โดยไม่จำเป็นต้องเป็นสองมิติ

คลาสของแบบจำลองการถดถอยซอฟต์แม็กซ์ที่ได้จะออกมาเป็นแบบนี้
ลองนำมาใช้งานโดยใช้ข้อมูลชุดเดิมและให้แสดงผลเหมือนเดิม
ผลที่ได้จะออกมาเหมือนกับตอนที่ไม่ใช้คลาส



ต่อมาลองทดสอบกับข้อมูลอื่น เช่นใช้ datasets.make_blobs ของ sklearn ดังที่ได้เคยลองใช้ใน https://phyblas.hinaboshi.com/20161127


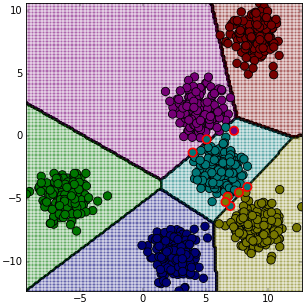
ลองทดสอบใช้กับข้อมูลที่มีมิติสูงขึ้นดูด้วย เช่น ลองจำแนกข้อมูล ๑๕ มิติเป็น ๕ กลุ่ม คราวนี้แสดงแค่กราฟความคืบหน้าในการเรียนรู้




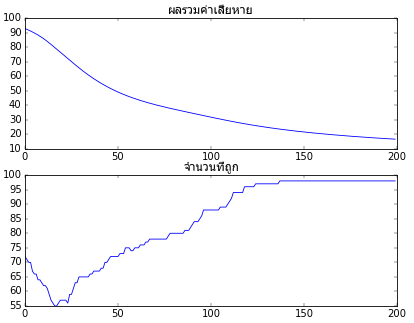
เท่านี้เราก็สามารถเขียนโปรแกรมเพื่อจำแนกประเภทข้อมูลอย่างง่ายได้แล้ว

ที่จริงยังมีอะไรต้องปรับปรุงอีกมากมายเพื่อให้เหมาะแก่การใช้งานจริงมากขึ้น ที่สำคัญอย่างหนึ่งก็คือการเปลี่ยนฟังก์ชันค่าเสียหาย ซึ่งในตัวอย่างที่ผ่านๆมาเราใช้เป็นผลรวมความคลาดเคลื่อนกำลังสอง แต่โดยทั่วไปแล้วเอนโทรปีไขว้ (cross entropy) เป็นที่นิยมมากกว่า

จากตัวอย่างในบทความนี้จะเห็นว่าสมการและโค้ดในส่วนคำนวณความชันนั้นดูแล้วยุ่งยากซับซ้อน แต่หากใช้เอนโทรปีไขว้เป็นฟังก์ชันค่าเสียหายแทนก็จะดูซับซ้อนน้อยลง เหมาะแก่การใช้งานจริงมากกว่า

อ่านต่อเรื่องการปรับแก้เป็นใช้เอนโทรปีไขว้ได้ที่ https://phyblas.hinaboshi.com/20161207



อ้างอิง

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --sql --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา บันทึก เรื่องแต่ง ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文