[python] วิเคราะห์การถดถอยโดยใช้ฟังก์ชันฐาน
เขียนเมื่อ 2018/07/20 18:50
แก้ไขล่าสุด 2024/10/03 19:33
เมื่อต้องการหาความสัมพันธ์อะไรบางอย่างระหว่างตัวแปรต้นและตัวแปรตามจากข้อมูลชุดหนึ่งที่มี เรียกปัญหานี้ว่าการวิเคราะห์การถดถอย (回归, regression)
เช่นสมมุติว่ามีตัวแปร ๒ ตัว ตัวแปรตั้งต้น x และตัวแปรตาม z มีความสัมพันธ์แบบนี้
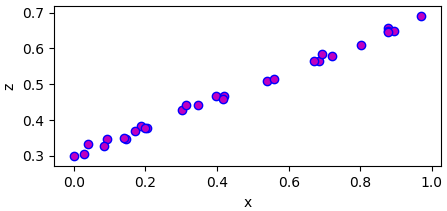
เนื่องจากข้อมูลนี้ตัวแปรทั้ง ๒ ดูแล้วสามารถลากเส้นตรงเพื่ออธิบายได้ ดังนั้นจึงสามารถใช้การวิเคราะห์การถดถอยเชิงเส้น (线性回归, linear regression) นั่นคือเขียน z ในรูปของ
..(1)
โดย w และ b เป็นค่าคงที่บางอย่างที่ต้องหา โดยอาศัยข้อมูล เช่นตัวอย่างนี้จะได้ว่า w=0.3 และ b=0.4 และจะสามารถคำนวณลากเส้นได้ผ่านกลางจุดข้อมูลแบบนี้
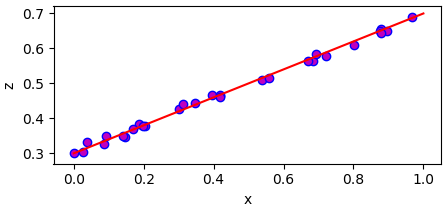
เรื่องของการวิเคราะห์การถดถอยเชิงเส้นได้เขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/20161210
แต่ในปัญหาโดยทั่วไปแล้วยากที่จะอธิบายด้วยเส้นตรงง่ายๆแบบนั้น เช่นหากข้อมูลมีหน้าตาแบบนี้
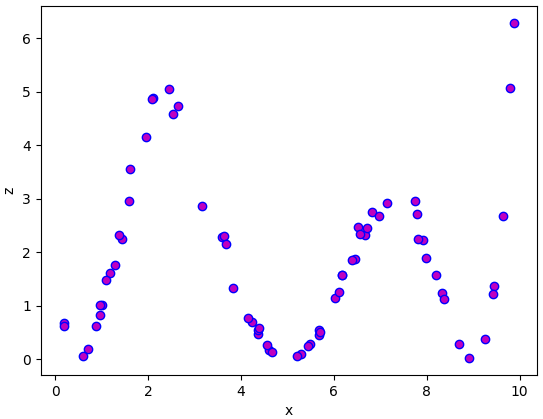
แบบนี้แทนที่จะแค่อธิบายด้วยเส้นตรง wx+b ง่ายๆ ควรใช้ฟังก์ชันอะไรบางอย่างที่ซับซ้อนกว่านั้น
ทางหนึ่งที่สามารถทำได้ก็คือ ใช้ฟังก์ชันฐาน (基函数, basis function)
คือ z อาจเขียนอยู่ในรูปของฟังก์ชันอะไรบางอย่างของ x มาบวกกัน อาจเขียนได้ในลักษณะแบบนี้
..(2)
โดย ϕi(x) คือฟังก์ชันฐาน คือเป็นกลุ่มฟังก์ชันอะไรสักอย่างของ x ที่ต้องการนำมาใช้อธิบายค่า โดยที่ ϕ แต่ละค่านั้นจะมีคุณสมบัติตั้งฉากซึ่งกันและกัน (正交, orthogonal) คือไม่สามารถเขียนตัวนึงในรูปของตัวอื่นๆบวกกันได้
ส่วน wi เป็นค่าน้ำหนักที่บ่งบอกว่าฟังก์ชันฐานแต่ละตัวมีความสำคัญแค่ไหน
และ m คือจำนวนฟังก์ชันฐานที่ใช้
ตัวอย่างฟังก์ชันฐานที่นิยมใช้ที่สุดก็คือ ฟังก์ชันพหุนาม นั่นคือ
..(3)
ก็จะได้ว่า
..(4)
ทีนี้เพื่อความสะดวกในการคำนวณ เราอาจเขียนใหม่ในรูปเวกเตอร์ได้เป็นแบบนี้
..(5)
โดย
..(6)
..(7)
สำหรับฟังก์ชันฐานพหุนาม
..(8)
ทีนี้จะเห็นว่าค่า z ที่คำนวณได้นั้นจะขึ้นอยู่กับ w ทั้งหลาย ดังนั้นปัญหาต่อไปก่อนอื่นสิ่งที่จะต้องทำก็คือหาค่า w ที่จะทำให้คำนวณค่า z ออกมาได้ใกล้เคียงกับข้อมูลที่มีอยู่มากที่สุด
การแก้หาค่า w นั้นอาจมีอยู่หลายวิธี แต่โดยทั่วไปที่เป็นพื้นฐานง่ายที่สุดก็คือคำนวณค่าผลรวมความคลาดเคลื่อนกำลังสอง (和方差, sum of squared error, SSE) ระหว่างค่าจริงกับค่าที่คำนวณได้
..(9)
ทีนี้ เมื่อเราจำเป็นต้องคำนวณค่า z สำหรับค่า x ทุกตัวที่มี โดยทั่วไปแล้วทางที่สะดวกคือเขียนอยู่ในรูปของการคูณเมทริกซ์ แบบนี้
..(10)
โดย
..(11)
โดย n คือจำนวนจุดข้อมูล
และ
..(12)
เมทริกซ์ของ Φ นี้มีชื่อเรียกเฉพาะว่าเมทริกซ์ออกแบบ (设计矩阵, design matrix)
แทนลงในสมการ (9) จะได้ว่า
..(13)
เป้าหมายคือต้องการหาค่า w ที่ทำให้ J ต่ำสุด โดยทั่วไปที่จุดต่ำสุดจะมีค่าความชันเป็น 0 ดังนั้นจึงหาอนุพันธ์ย่อยของ J เทียบ w และให้เท่ากับ 0 จะได้
..(14)
แล้วก็จะได้ว่า
..(15)
ซึ่งในรูปแบบนี้สามารถหาค่า w ได้ด้วยการแก้ระบบสมการ
ในไพธอนมีฟังก์ชัน np.linalg.solve ซึ่งใช้สำหรับแก้สมการแบบนี้ได้ทันทีอยู่แล้ว จึงดึงมาใช้ได้เลย เสร็จแล้วก็จะได้ค่า w ที่ต้องการออกมา
เสร็จแล้วพอได้ w มาก็นำมาหาค่า z ของข้อมูลใหม่ได้โดยสมการ (10) ต่อไป
สรุปขั้นตอนสำหรับการหาค่า z ใหม่ที่ไม่รู้คือ
1. คำนวณ Φ ของข้อมูล x ที่มี
2. ใช้ np.linalg.solve แก้หาค่า w
3. คำนวณ Φ ของข้อมูล x ใหม่ที่ต้องการหา
4. คำนวณ z จาก Φ ใหม่และ w
ลองเขียนโค้ดเพื่อใช้งานดูเลย ข้อมูลตัวอย่างที่ใช้นี้เป็นอันเดียวกับที่แสดงในภาพข้างบน ในที่นี้ใช้ x และ z เป็นตัวแปรของข้อมูลที่มี ส่วน x_ เป็นข้อมูลจุดใหม่ที่ต้องการหา z_ เป็นค่าของจุดใหม่ที่คำนวณได้ ส่วน Φ เขียนแทนด้วย phi
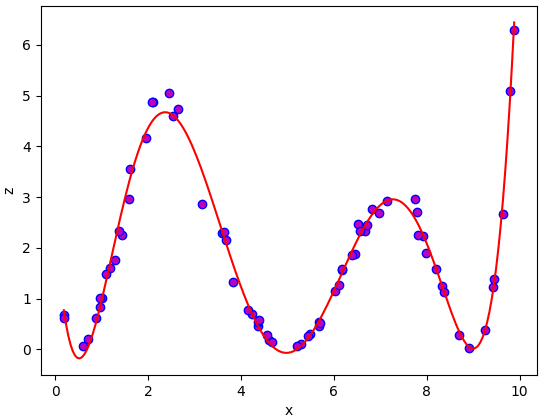
กรณีที่ใช้ฐานเป็นพหุนามแบบนี้อาจเรียกว่าการวิเคราะห์การถดถอยพหุนาม (多项式回归, polynomial regression)
เพื่อความสะดวกในการใช้ ลองเขียนในรูปแบบคลาสได้ดังนี้
ที่จริงเรื่องการวิเคราะห์การถดถอยพหุนามเคยเขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/20161219
เพียงแต่ว่ารูปแบบการเขียน และวิธีการหาค่า w ก็ต่างกัน ในนั้นใช้วิธีการเคลื่อนลงตามความชัน (梯度下降法, gradient descent) แต่ในนี้ใช้วิธีการแก้สมการหาโดยตรง
ใช้ฟังก์ชันเกาส์เป็นฐาน
นอกจากพหุนามแล้ว ฐานอีกชนิดหนึ่งที่นิยมคือใช้ฟังก์ชันเกาส์ (Gauss)
ฟังก์ชันเกาส์ เป็นฟังก์ชันที่มีค่าเป็นลักษณะระฆังคว่ำ โดยมีค่าสูงสุดอยู่ที่จุดนึง เรียกว่าเป็นจุดศูนย์กลาง และยิ่งห่างจากจุดนี้ไปก็จะมีค่าต่ำลงเรื่อยๆจนเข้าใกล้ 0 นิยามดังนี้
..(16)
โดย μ คือจุดศูนย์กลาง ส่วน γ เป็นตัวกำหนดว่าค่าจะลงลงเร็วแค่ไหนเมื่อห่างจากใจกลาง ยิ่งค่าน้อยยิ่งลดลงช้า
เมื่อนำมาใช้เป็นฟังก์ชันฐาน ฐานเกาส์อาจนิยามตามนี้
..(17)
โดย xj เป็นจุดข้อมูล นั่นคือใช้จุดข้อมูลแต่ละจุดเป็นศูนย์กลางของฐานแต่ละอัน
กรณีนี้เราจะมีจำนวนฐานเท่ากับจำนวนข้อมูลทั้งหมดที่ใช้
เขียนโปรแกรมได้ดังนี้
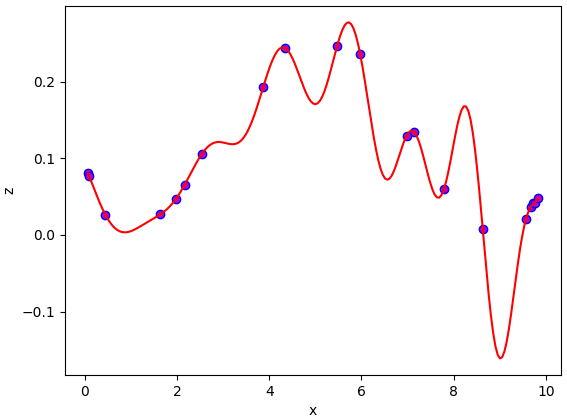
ผลที่ได้จะพบว่าออกมาแปลกๆ ที่เป็นแบบนี้เพราะว่าเมื่อจำนวนฐานเท่ากับจำนวนข้อมูลจะทำให้ฟังก์ชันที่ได้สามารถลากผ่านจุดข้อมูลทั้งหมด
ซึ่งที่จริงแล้วข้อมูลโดยทั่วไปจะมีความไม่แน่นอนปนอยู่ ดังนั้นการฝืนให้เส้นลากผ่านจุดทั้งหมดนั้นจึงไม่ใช่เรื่องที่ดี มีแต่จะทำให้เกิดการเรียนรู้เกิน (过学习, overlearning) คือการที่ผลการคำนวณปรับตัวเข้ากับข้อมูลที่มีอยู่มากเกินไปแต่ไม่สามารถใช้อธิบายทุกอย่างตามธรรมชาติจริงๆได้
เมื่อเป็นแบบนี้จึงจำเป็นต้องมีการเรกูลาไรซ์ (正规化, regularize) คือการทำให้การคำนวณไม่ยึดติดกับข้อมูลที่มีมากเกินไป
เกี่ยวกับแนวคิดของการเรกูลาไรซ์เคยเขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/20170928
ในที่นี้ใช้เรกูลาไรซ์แบบ l2 สมการ (13) ก็จะแก้เป็น
..(18)
ที่เปลี่ยนไปคือมีเพิ่มพจน์ทางขวาบวกเข้ามา โดย λ คือขนาดของการเรกูลาไรซ์
จากนั้นก็ให้ความชันเท่ากับ 0 เช่นเคย
..(19)
แล้วก็จะได้
..(20)
โดย I คือเมทริกซ์เอกลักษณ์ ค่า λ ที่เพิ่มเข้าไปจะมีผลทำให้ค่าแนวทแยงของเมทริกซ์มากขึ้น
สามารถเขียนโค้ดแก้ตรงที่คำนวณ w ใหม่ เป็นแบบนี้
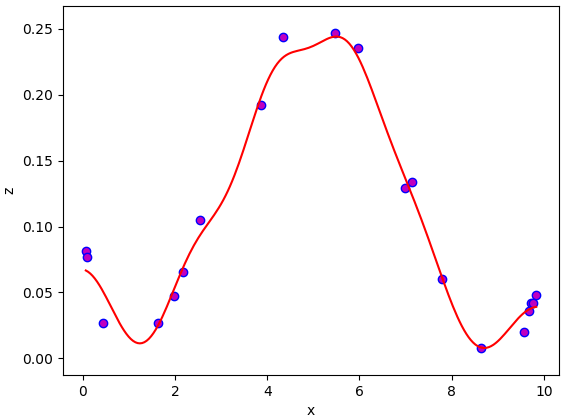
จะเห็นว่าได้เส้นกราฟออกมาเรียบและดูสมเหตุสมผลขึ้น
สุดท้ายนี้ เพื่อความสะดวกในการใช้งานลองมาสร้างเป็นคลาสขึ้นมาดู
ข้อควรสังเกตอย่างหนึ่งคือ กรณีนี้จำเป็นต้องบันทึกตำแหน่งของ x ที่ป้อนเข้ามาตอนแรกไว้ด้วย เพราะต้องใช้ตำแหน่งใจกลางของฐานเกาส์ในการคำนวณ
ขอยกตัวอย่างการใช้ด้วยการเปรียบเทียบความแตกต่างระหว่างกรณีที่ λ มีค่าต่างกัน
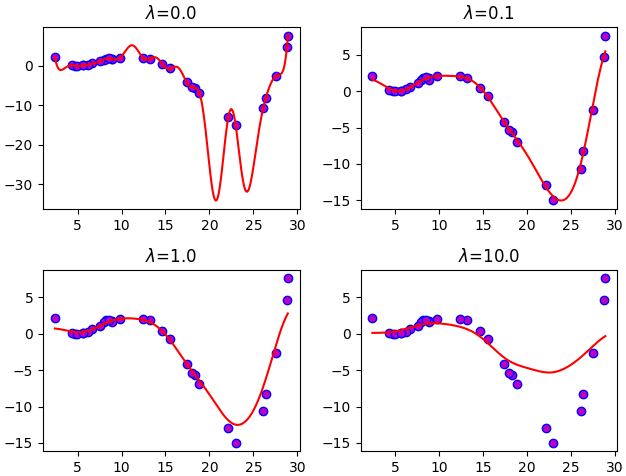
จะเห็นได้ว่าเมื่อ λ น้อยไปจะทำให้เกิดการเรียนรู้เกินได้ง่าย แต่พอมากไปก็จะทำให้ไม่สามารถปรับเข้ากับข้อมูลได้ดีพอ ดังนั้นการเลือก λ ที่เหมาะสมจึงสำคัญ
ทั้งหมดนี้เป็นพื้นฐานของการประยุกต์ใช้ฟังก์ชันฐานในปัญหาการวิเคราะห์การถดถอย
การใช้ฟังก์ชันฐานยังเป็นพื้นฐานสำคัญที่จะต่อยอดไปยังเรื่องอื่นในเทคทิคการเรียนรู้ของเครื่อง เช่นการถดถอยเชิงเส้นแบบเบส์ (贝叶斯线性回归, Bayesian Linear Regression) รวมทั้งการใช้ลูกเล่นเคอร์เนล (核技巧, kernel trick)
เกี่ยวกับลูกเล่นเคอร์เนลอ่านได้ใน https://phyblas.hinaboshi.com/20180724
อ้างอิง
เช่นสมมุติว่ามีตัวแปร ๒ ตัว ตัวแปรตั้งต้น x และตัวแปรตาม z มีความสัมพันธ์แบบนี้

เนื่องจากข้อมูลนี้ตัวแปรทั้ง ๒ ดูแล้วสามารถลากเส้นตรงเพื่ออธิบายได้ ดังนั้นจึงสามารถใช้การวิเคราะห์การถดถอยเชิงเส้น (线性回归, linear regression) นั่นคือเขียน z ในรูปของ
..(1)
โดย w และ b เป็นค่าคงที่บางอย่างที่ต้องหา โดยอาศัยข้อมูล เช่นตัวอย่างนี้จะได้ว่า w=0.3 และ b=0.4 และจะสามารถคำนวณลากเส้นได้ผ่านกลางจุดข้อมูลแบบนี้

เรื่องของการวิเคราะห์การถดถอยเชิงเส้นได้เขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/20161210
แต่ในปัญหาโดยทั่วไปแล้วยากที่จะอธิบายด้วยเส้นตรงง่ายๆแบบนั้น เช่นหากข้อมูลมีหน้าตาแบบนี้

แบบนี้แทนที่จะแค่อธิบายด้วยเส้นตรง wx+b ง่ายๆ ควรใช้ฟังก์ชันอะไรบางอย่างที่ซับซ้อนกว่านั้น
ทางหนึ่งที่สามารถทำได้ก็คือ ใช้ฟังก์ชันฐาน (基函数, basis function)
คือ z อาจเขียนอยู่ในรูปของฟังก์ชันอะไรบางอย่างของ x มาบวกกัน อาจเขียนได้ในลักษณะแบบนี้
..(2)
โดย ϕi(x) คือฟังก์ชันฐาน คือเป็นกลุ่มฟังก์ชันอะไรสักอย่างของ x ที่ต้องการนำมาใช้อธิบายค่า โดยที่ ϕ แต่ละค่านั้นจะมีคุณสมบัติตั้งฉากซึ่งกันและกัน (正交, orthogonal) คือไม่สามารถเขียนตัวนึงในรูปของตัวอื่นๆบวกกันได้
ส่วน wi เป็นค่าน้ำหนักที่บ่งบอกว่าฟังก์ชันฐานแต่ละตัวมีความสำคัญแค่ไหน
และ m คือจำนวนฟังก์ชันฐานที่ใช้
ตัวอย่างฟังก์ชันฐานที่นิยมใช้ที่สุดก็คือ ฟังก์ชันพหุนาม นั่นคือ
..(3)
ก็จะได้ว่า
..(4)
ทีนี้เพื่อความสะดวกในการคำนวณ เราอาจเขียนใหม่ในรูปเวกเตอร์ได้เป็นแบบนี้
..(5)
โดย
..(6)
..(7)
สำหรับฟังก์ชันฐานพหุนาม
..(8)
ทีนี้จะเห็นว่าค่า z ที่คำนวณได้นั้นจะขึ้นอยู่กับ w ทั้งหลาย ดังนั้นปัญหาต่อไปก่อนอื่นสิ่งที่จะต้องทำก็คือหาค่า w ที่จะทำให้คำนวณค่า z ออกมาได้ใกล้เคียงกับข้อมูลที่มีอยู่มากที่สุด
การแก้หาค่า w นั้นอาจมีอยู่หลายวิธี แต่โดยทั่วไปที่เป็นพื้นฐานง่ายที่สุดก็คือคำนวณค่าผลรวมความคลาดเคลื่อนกำลังสอง (和方差, sum of squared error, SSE) ระหว่างค่าจริงกับค่าที่คำนวณได้
..(9)
ทีนี้ เมื่อเราจำเป็นต้องคำนวณค่า z สำหรับค่า x ทุกตัวที่มี โดยทั่วไปแล้วทางที่สะดวกคือเขียนอยู่ในรูปของการคูณเมทริกซ์ แบบนี้
..(10)
โดย
..(11)
โดย n คือจำนวนจุดข้อมูล
และ
..(12)
เมทริกซ์ของ Φ นี้มีชื่อเรียกเฉพาะว่าเมทริกซ์ออกแบบ (设计矩阵, design matrix)
แทนลงในสมการ (9) จะได้ว่า
..(13)
เป้าหมายคือต้องการหาค่า w ที่ทำให้ J ต่ำสุด โดยทั่วไปที่จุดต่ำสุดจะมีค่าความชันเป็น 0 ดังนั้นจึงหาอนุพันธ์ย่อยของ J เทียบ w และให้เท่ากับ 0 จะได้
..(14)
แล้วก็จะได้ว่า
..(15)
ซึ่งในรูปแบบนี้สามารถหาค่า w ได้ด้วยการแก้ระบบสมการ
ในไพธอนมีฟังก์ชัน np.linalg.solve ซึ่งใช้สำหรับแก้สมการแบบนี้ได้ทันทีอยู่แล้ว จึงดึงมาใช้ได้เลย เสร็จแล้วก็จะได้ค่า w ที่ต้องการออกมา
เสร็จแล้วพอได้ w มาก็นำมาหาค่า z ของข้อมูลใหม่ได้โดยสมการ (10) ต่อไป
สรุปขั้นตอนสำหรับการหาค่า z ใหม่ที่ไม่รู้คือ
1. คำนวณ Φ ของข้อมูล x ที่มี
2. ใช้ np.linalg.solve แก้หาค่า w
3. คำนวณ Φ ของข้อมูล x ใหม่ที่ต้องการหา
4. คำนวณ z จาก Φ ใหม่และ w
ลองเขียนโค้ดเพื่อใช้งานดูเลย ข้อมูลตัวอย่างที่ใช้นี้เป็นอันเดียวกับที่แสดงในภาพข้างบน ในที่นี้ใช้ x และ z เป็นตัวแปรของข้อมูลที่มี ส่วน x_ เป็นข้อมูลจุดใหม่ที่ต้องการหา z_ เป็นค่าของจุดใหม่ที่คำนวณได้ ส่วน Φ เขียนแทนด้วย phi
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)
n = 70 # จำนวนข้อมูล
x = np.random.uniform(0,10,n) # จุดข้อมูลที่รู้ค่า
# ค่าของแต่ละจุด ให้เป็นฟังก์ชันพหุนามที่บวกคลื่นรบกวนเข้าไป
z = ((2*x-1)**2*(x-5)**2*(x-9)**2)*np.random.normal(1,0.1,n)/1000
# ฟังก์ชันสำหรับสร้าง Φ โดยใช้ฐานเป็นพหุนาม
def than_phahunam(x,m):
return np.array([x**i for i in range(m)]).T
m = 8 # จำนวนฐานที่จะใช้
phi = than_phahunam(x,m)
# แก้สมการหาค่า w
w = np.linalg.solve(phi.T.dot(phi),phi.T.dot(z))
x_ = np.linspace(x.min(),x.max(),201) # ข้อมูลใหม่ที่ต้องการหาค่า
phi_ = than_phahunam(x_,m)
z_ = phi_.dot(w)
plt.axes(xlabel='x',ylabel='z')
plt.scatter(x,z,c='m',edgecolor='b')
plt.plot(x_,z_,'r')
plt.show()
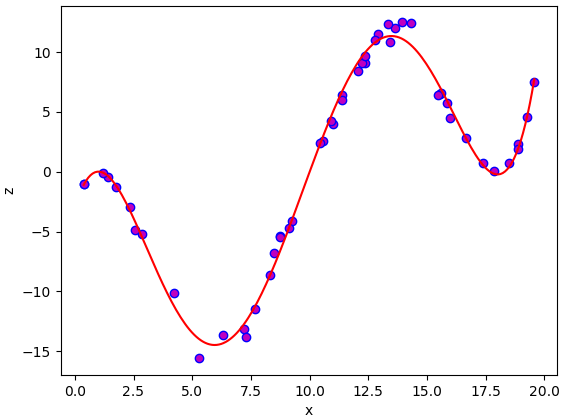
กรณีที่ใช้ฐานเป็นพหุนามแบบนี้อาจเรียกว่าการวิเคราะห์การถดถอยพหุนาม (多项式回归, polynomial regression)
เพื่อความสะดวกในการใช้ ลองเขียนในรูปแบบคลาสได้ดังนี้
class ThotthoiPhahunam:
def __init__(self,m=4):
self.m = m
def rianru(self,x,z):
phi = self.than(x)
self.w = np.linalg.solve(phi.T.dot(phi),phi.T.dot(z))
def thamnai(self,x_):
phi_ = self.than(x_)
return phi_.dot(self.w)
def than(self,x):
return x[:,None]**np.arange(self.m)
np.random.seed(0)
n = 50
x = np.random.uniform(0,20,n)
z = ((x-1)**2*(x-10)*(x-18)**2)*np.random.normal(1,0.1,n)/1000
tt = ThotthoiPhahunam(m=8)
tt.rianru(x,z)
x_ = np.linspace(x.min(),x.max(),201)
z_ = tt.thamnai(x_)
plt.axes(xlabel='x',ylabel='z')
plt.scatter(x,z,c='m',edgecolor='b')
plt.plot(x_,z_,'r')
plt.show()
ที่จริงเรื่องการวิเคราะห์การถดถอยพหุนามเคยเขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/20161219
เพียงแต่ว่ารูปแบบการเขียน และวิธีการหาค่า w ก็ต่างกัน ในนั้นใช้วิธีการเคลื่อนลงตามความชัน (梯度下降法, gradient descent) แต่ในนี้ใช้วิธีการแก้สมการหาโดยตรง
ใช้ฟังก์ชันเกาส์เป็นฐาน
นอกจากพหุนามแล้ว ฐานอีกชนิดหนึ่งที่นิยมคือใช้ฟังก์ชันเกาส์ (Gauss)
ฟังก์ชันเกาส์ เป็นฟังก์ชันที่มีค่าเป็นลักษณะระฆังคว่ำ โดยมีค่าสูงสุดอยู่ที่จุดนึง เรียกว่าเป็นจุดศูนย์กลาง และยิ่งห่างจากจุดนี้ไปก็จะมีค่าต่ำลงเรื่อยๆจนเข้าใกล้ 0 นิยามดังนี้
..(16)
โดย μ คือจุดศูนย์กลาง ส่วน γ เป็นตัวกำหนดว่าค่าจะลงลงเร็วแค่ไหนเมื่อห่างจากใจกลาง ยิ่งค่าน้อยยิ่งลดลงช้า
เมื่อนำมาใช้เป็นฟังก์ชันฐาน ฐานเกาส์อาจนิยามตามนี้
..(17)
โดย xj เป็นจุดข้อมูล นั่นคือใช้จุดข้อมูลแต่ละจุดเป็นศูนย์กลางของฐานแต่ละอัน
กรณีนี้เราจะมีจำนวนฐานเท่ากับจำนวนข้อมูลทั้งหมดที่ใช้
เขียนโปรแกรมได้ดังนี้
def gauss(x1,x2,gamma):
return np.exp(-gamma*(x1-x2)**2)
n = 20
np.random.seed(4)
x = np.random.uniform(0,10,n)
z = ((x-1)**2*(x-9)**2)*np.random.normal(1,0.1,n)/1000
gamma = 1
phi = gauss(x,x[:,None],gamma)
w = np.linalg.solve(phi.T.dot(phi),phi.T.dot(z))
x_ = np.linspace(x.min(),x.max(),201)
phi_ = gauss(x,x_[:,None],gamma)
z_ = phi_.dot(w)
plt.axes(xlabel='x',ylabel='z')
plt.scatter(x,z,c='m',edgecolor='b')
plt.plot(x_,z_,'r')
plt.show()
ผลที่ได้จะพบว่าออกมาแปลกๆ ที่เป็นแบบนี้เพราะว่าเมื่อจำนวนฐานเท่ากับจำนวนข้อมูลจะทำให้ฟังก์ชันที่ได้สามารถลากผ่านจุดข้อมูลทั้งหมด
ซึ่งที่จริงแล้วข้อมูลโดยทั่วไปจะมีความไม่แน่นอนปนอยู่ ดังนั้นการฝืนให้เส้นลากผ่านจุดทั้งหมดนั้นจึงไม่ใช่เรื่องที่ดี มีแต่จะทำให้เกิดการเรียนรู้เกิน (过学习, overlearning) คือการที่ผลการคำนวณปรับตัวเข้ากับข้อมูลที่มีอยู่มากเกินไปแต่ไม่สามารถใช้อธิบายทุกอย่างตามธรรมชาติจริงๆได้
เมื่อเป็นแบบนี้จึงจำเป็นต้องมีการเรกูลาไรซ์ (正规化, regularize) คือการทำให้การคำนวณไม่ยึดติดกับข้อมูลที่มีมากเกินไป
เกี่ยวกับแนวคิดของการเรกูลาไรซ์เคยเขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/20170928
ในที่นี้ใช้เรกูลาไรซ์แบบ l2 สมการ (13) ก็จะแก้เป็น
..(18)
ที่เปลี่ยนไปคือมีเพิ่มพจน์ทางขวาบวกเข้ามา โดย λ คือขนาดของการเรกูลาไรซ์
จากนั้นก็ให้ความชันเท่ากับ 0 เช่นเคย
..(19)
แล้วก็จะได้
..(20)
โดย I คือเมทริกซ์เอกลักษณ์ ค่า λ ที่เพิ่มเข้าไปจะมีผลทำให้ค่าแนวทแยงของเมทริกซ์มากขึ้น
สามารถเขียนโค้ดแก้ตรงที่คำนวณ w ใหม่ เป็นแบบนี้
l = 0.1
w = np.linalg.solve(phi.T.dot(phi) + np.eye(len(x))*l,phi.T.dot(z))
จะเห็นว่าได้เส้นกราฟออกมาเรียบและดูสมเหตุสมผลขึ้น
สุดท้ายนี้ เพื่อความสะดวกในการใช้งานลองมาสร้างเป็นคลาสขึ้นมาดู
class ThotthoiThanGauss:
def __init__(self,gamma=1,l=0.1):
self.gamma = gamma
self.l = l
def rianru(self,x,z):
phi = self.gauss(x,x[:,None])
self.w = np.linalg.solve(phi.T.dot(phi)+self.l*np.eye(len(x)),phi.T.dot(z))
self.x = x
def thamnai(self,x_):
phi_ = self.gauss(self.x,x_[:,None])
return phi_.dot(self.w)
def gauss(self,x1,x2):
return np.exp(-self.gamma*(x1-x2)**2)ข้อควรสังเกตอย่างหนึ่งคือ กรณีนี้จำเป็นต้องบันทึกตำแหน่งของ x ที่ป้อนเข้ามาตอนแรกไว้ด้วย เพราะต้องใช้ตำแหน่งใจกลางของฐานเกาส์ในการคำนวณ
ขอยกตัวอย่างการใช้ด้วยการเปรียบเทียบความแตกต่างระหว่างกรณีที่ λ มีค่าต่างกัน
n = 30
np.random.seed(5)
x = np.random.uniform(0,30,n)
z = ((x-5)**2*(x-15)*(x-28))*np.random.normal(1,0.2,n)/1000
x_ = np.linspace(x.min(),x.max(),301)
ll = [0,0.1,1,10]
plt.figure(figsize=[6.5,5])
for i in range(4):
l = ll[i]
tt = ThotthoiThanGauss(gamma=0.1,l=l)
tt.rianru(x,z)
z_ = tt.thamnai(x_)
plt.subplot(2,2,i+1)
plt.scatter(x,z,c='m',edgecolor='b')
plt.title('$\\lambda$=%.1f'%l)
plt.plot(x_,z_,'r')
plt.tight_layout()
plt.show()
จะเห็นได้ว่าเมื่อ λ น้อยไปจะทำให้เกิดการเรียนรู้เกินได้ง่าย แต่พอมากไปก็จะทำให้ไม่สามารถปรับเข้ากับข้อมูลได้ดีพอ ดังนั้นการเลือก λ ที่เหมาะสมจึงสำคัญ
ทั้งหมดนี้เป็นพื้นฐานของการประยุกต์ใช้ฟังก์ชันฐานในปัญหาการวิเคราะห์การถดถอย
การใช้ฟังก์ชันฐานยังเป็นพื้นฐานสำคัญที่จะต่อยอดไปยังเรื่องอื่นในเทคทิคการเรียนรู้ของเครื่อง เช่นการถดถอยเชิงเส้นแบบเบส์ (贝叶斯线性回归, Bayesian Linear Regression) รวมทั้งการใช้ลูกเล่นเคอร์เนล (核技巧, kernel trick)
เกี่ยวกับลูกเล่นเคอร์เนลอ่านได้ใน https://phyblas.hinaboshi.com/20180724
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib