[python] วิเคราะห์การถดถอยพหุนาม
เขียนเมื่อ 2016/12/19 10:43
แก้ไขล่าสุด 2021/09/28 16:42
ก่อนหน้านี้ได้เขียนถึงการวิเคราะห์การถดถอยเชิงเส้นในหนึ่งมิติไป https://phyblas.hinaboshi.com/20161210
แต่ว่าการวิเคราะห์การถดถอยเชิงเส้นนั้นสามารถแก้ได้แต่ปัญหาที่เป็นเชิงเส้น นั่นคืออยู่ในรูป z = w*x + b
ปัญหาโดยทั่วไปอาจไม่ได้เรียบง่ายอยู่ในรูปแบบเชิงเส้นให้เราแก้ได้ง่ายๆ เช่นลองยกตัวอย่างข้อมูลในลักษณะนี้
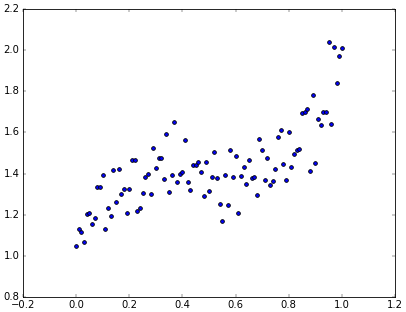
แบบนี้ย่อมไม่ควรจะใช้การถดถอยเชิงเส้นได้
หากต้องการปัญหาที่ผลเฉลยไม่น่าจะเป็นเชิงเส้น ก็ต้องปรับวิธีใหม่ซึ่งซับซ้อนขึ้น
รูปแบบคำตอบที่ง่ายรองลงมาจากเชิงเส้นธรรมดาก็คืออยู่ในรูปพหุนาม นั่นคือเป็นลักษณะแบบนี้
รูปแบบสมการลักษณะนี้ดูแล้วก็จะคล้ายกับสมการเชิงเส้นหลายมิติ ซึ่งเขียนถึงไปใน https://phyblas.hinaboshi.com/20161212
เพียงแต่ว่าเปลี่ยนจาก x1 เป็น x**1 ส่วน x2 เป็น x**2 และ xn เป็น x**n
นั่นหมายความว่าถ้าใช้แนวคิดเดียวกันเราก็สามารถแก้ปัญหาพหุนามได้ โดยให้ถือว่า x, x**2 และ x**3 ล้วนเป็นตัวแปรต้นคนละตัว โดย x1 เป็น x และ x2 เป็น x**2 แบบนี้
เราจะลองมาสร้างแบบจำลองการวิเคราะห์การถดถอยพหุนามเพื่อแก้ปัญหาข้อนี้กันดู
ก่อนอื่นเริ่มจากเฉลยว่าข้อมูลที่วาดในรูปข้างต้นมาจากโค้ดนี้
ซึ่งดูจากตรงนี้จะเห็นว่าคำตอบที่ควรจะเป็นก็คือ w0=5, w1=21, w2=31 และ w3=1
เช่นเคย คราวนี้เราก็จะมาดูว่าวิธีการที่เราใช้จะสามารถหาคำตอบได้ตามนี้หรือเปล่า
ก่อนอื่นที่น่าพูดถึงคือวิธีการสร้างข้อมูลตัวแปรต้น โดยเดิมทีเรามีแค่ x ตัวเดียว แต่ว่าต้องสร้างค่า x ที่ยกกำลังต่างๆตั้งแต่ 0 ไปจนถึงดีกรีที่ต้องการ
อาจใช้วิธีการดังนี้
ได้
หลักแรกคือพจน์ x0 ซึ่งจะไปคูณกับ w0 จะเป็น 1 ทั้งหมด ปกติแล้ว w0 คือไบแอสซึ่งไม่ต้องการนำไปคูณกับค่า x ตัวใดๆ แต่ในที่นี้เราสร้างแถว x0 ออกมาด้วย แทนที่จะแยกค่าไบแอสออกมา
ใช้วิธีการนี้เราสามารถเขียนคลาสสำหรับการวิเคราะห์การถดถอยพหุนามแบบตัวแปรเดียวได้ดังนี้
โดยในนี้เราให้กำหนดค่าดีกรีในพารามิเตอร์ deg ตอนที่สร้างออบเจ็กต์พร้อมกับค่าอัตราการเรียนรู้
เวลาป้อนค่าตัวแปรต้นก็ใส่ค่า x ซึ่งเป็นอาเรย์มิติเดียวไป แล้วก็จะถูกแปลงเป็นพหุนามเพื่อทำการเรียนรู้ต่อไป
ลองนำมาใช้กับค่า x และ z ของโจทย์ข้อนี้ที่เราเตรียมเอาไว้ โดยสร้างออบเจ็กต์จากนั้นใช้เมธอด rianru
จากนั้นลองดูค่าน้ำหนักที่ได้
ก็จะได้ค่าน้ำหนักใกล้เคียงกับที่เราใส่ตอนสร้างข้อมูลขึ้น
ทีนี้ลองวาดกราฟดูเทียบกับจุดข้อมูลที่ใช้เรียนรู้ โดยใช้เมธอด thamnai เพื่อหาค่าที่ทำนายโดยใช้ค่าน้ำหนักที่ได้
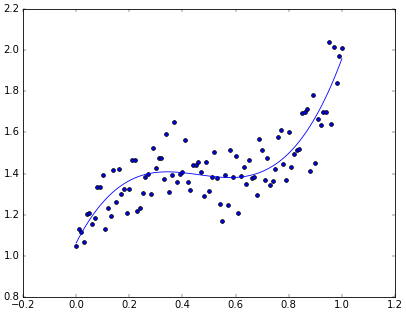
เส้นที่ทำนายขึ้นลากผ่านกลางจุดข้อมูลอย่างสวยงาม แสดงให้เห็นว่าการคำนวณถูกต้อง
ต่อมาลองคิดกรณีที่ปัญหาประกอบด้วย ๒ ตัวแปรต้นขึ้นไป ซึ่งจะซับซ้อนไปอีก
เช่นลองกรณีของสองมิติดังตัวอย่างนี้
ซึ่งประกอบด้วย ๖ พจน์ คือ 1,x,y,xx,xy,yy ตามลำดับ
กรณีแบบนี้เรียกว่าเป็นพหุนามดีกรี ๒ คือผลรวมเลขชี้กำลังสูงสุดไม่เกิน ๒ ถ้ามี x*x*x หรือ x*y*y อยู่ด้วยก็จะเป็นดีกรี ๓ เป็นต้น
ลองนำมาวาดภาพการกระจายในสามมิติดู
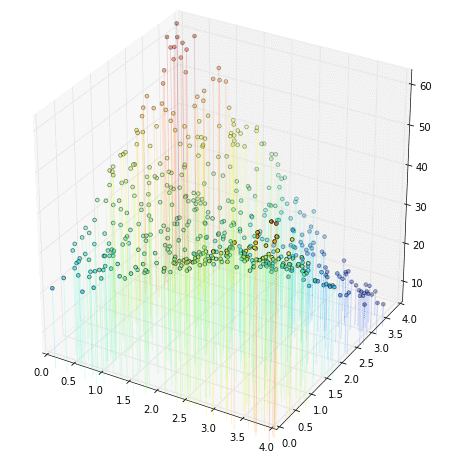
วิธีการสร้างตัวแปรต้นสำหรับมาใช้วิเคราะห์ถดถอยพหุนามนั้น สำหรับกรณีสองตัวแปรเราอาจเขียนแจกแจงพหุนามได้ดังนี้
***ใครงงกับรูปแบบการเขียนโค้ดตรงนี้อาจลองอ่านทวนเนื้อหา ไพธอนเบื้องต้น บทที่ ๙: การทำซ้ำด้วย for ตรงส่วนของการใช้ for ซ้อน for
ได้
โดยกรณีนี้เป็นดีกรี ๒ ค่าที่ได้แต่ละหลักจะเป็นพจน์ของ 1,x,y,xx,xy,yy ตามลำดับ
และถ้าหากเป็นดีกรี ๓ ก็จะมีพจน์ xxx,xxy,xyy,yyy เพิ่มเข้ามาอีก รวมเป็น ๑๐ หลัก เป็นต้น
การเขียนแบบนี้ดูแล้วยุ่งยากพอสมควร อีกทั้งถ้ามี ๓ ตัวแปรการเขียนก็จะยิ่งยุ่งยากขึ้นไปอีก
พอเป็นแบบนั้นแล้วลองหาตัวช่วยเพิ่มเติมอาจจะดีกว่า เช่น หากใช้ sklearn เข้าช่วยก็อาจสามารถทำได้ง่ายขึ้น
ในมอดูลย่อย preprocessing ของ sklearn มีคลาสที่ชื่อ PolynomialFeatures อยู่ มีไว้สำหรับทำในสิ่งเดียวกับที่เราเพิ่งทำไป
ขออธิบายด้วยการยกตัวอย่างการใช้งานจริงก่อน
การใช้ลองเขียนตามนี้
ก็จะได้ xy_ แบบเดียวกับที่ใช้วิธีอย่างในตอนแรก
การใช้ PolynomialFeatures จะคล้ายกับ StandardScaler ที่กล่าวถึงไปในเรื่องของการทำข้อมูลให้เป็นมาตรฐาน https://phyblas.hinaboshi.com/20161124
คือจะใช้เมธอด fit_transform ในลักษณะเดียวกัน นั่นคือเป็นการย่อขั้นตอนการใช้ เพื่อให้ไม่ต้องใช้ fit แล้วต่อด้วย transform อีกที หากเขียนแบบเต็มๆน่าจะเป็นแบบนี้
เมื่อใช้ PolynomialFeatures แบบนี้แล้วจะใช้กับปัญหาที่มีตัวแปรต้นกี่ตัวก็ได้ เช่นถ้าลองใช้กับ ๓ ตัวแปรดู แจกแจงถึงดีกรี ๒
ได้
ผลที่ได้มี ๑๐ พจน์ ตามนี้ 1, x1, x2, x3, x1x1, x1x2, x1x3, x2x2, x2x3, x3x3
เมื่อเข้าใจวิธีการแปลงตัวแปรต้นให้เป็นพหุนามแล้ว ก็ลองสร้างแบบจำลองขึ้นดู เขียนได้ดังนี้
ลักษณะคล้ายกับกรณีตัวแปรเดียวแต่ว่าค่า X ที่ต้องใส่ตอนที่เรียนรู้คราวนี้เป็นอาเรย์สองมิติ และใช้ PolynomialFeatures ในการทำให้เป็นพหุนาม โดยค่า deg จะกำหนดดีกรีที่ต้องการแปลง
นำมาใช้กับ x,y,z ที่เพิ่งเตรียมไว้จากตัวอย่างที่แล้ว แล้วลองวาดผลที่ได้ดู
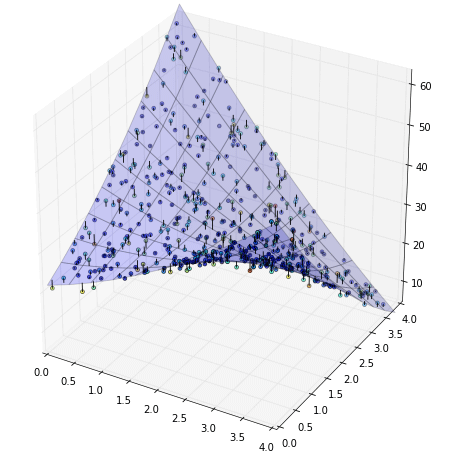
พื้นผิวค่าที่ได้ลากผ่านกลางระหว่างจุดแสดงว่าแทนคำตอบได้ดี
ลองดูค่าน้ำหนักที่ได้
ได้ค่าออกมาใกล้เคียงกับ [22,4,7,1,-6,1] ซึ่งเป็นคำตอบที่ควรเป็นจริงๆ
อ้างอิง
แต่ว่าการวิเคราะห์การถดถอยเชิงเส้นนั้นสามารถแก้ได้แต่ปัญหาที่เป็นเชิงเส้น นั่นคืออยู่ในรูป z = w*x + b
ปัญหาโดยทั่วไปอาจไม่ได้เรียบง่ายอยู่ในรูปแบบเชิงเส้นให้เราแก้ได้ง่ายๆ เช่นลองยกตัวอย่างข้อมูลในลักษณะนี้

แบบนี้ย่อมไม่ควรจะใช้การถดถอยเชิงเส้นได้
หากต้องการปัญหาที่ผลเฉลยไม่น่าจะเป็นเชิงเส้น ก็ต้องปรับวิธีใหม่ซึ่งซับซ้อนขึ้น
รูปแบบคำตอบที่ง่ายรองลงมาจากเชิงเส้นธรรมดาก็คืออยู่ในรูปพหุนาม นั่นคือเป็นลักษณะแบบนี้
z = w0 + w1*x + w2*x**2 + w3*x**3 + ...
รูปแบบสมการลักษณะนี้ดูแล้วก็จะคล้ายกับสมการเชิงเส้นหลายมิติ ซึ่งเขียนถึงไปใน https://phyblas.hinaboshi.com/20161212
เพียงแต่ว่าเปลี่ยนจาก x1 เป็น x**1 ส่วน x2 เป็น x**2 และ xn เป็น x**n
นั่นหมายความว่าถ้าใช้แนวคิดเดียวกันเราก็สามารถแก้ปัญหาพหุนามได้ โดยให้ถือว่า x, x**2 และ x**3 ล้วนเป็นตัวแปรต้นคนละตัว โดย x1 เป็น x และ x2 เป็น x**2 แบบนี้
เราจะลองมาสร้างแบบจำลองการวิเคราะห์การถดถอยพหุนามเพื่อแก้ปัญหาข้อนี้กันดู
ก่อนอื่นเริ่มจากเฉลยว่าข้อมูลที่วาดในรูปข้างต้นมาจากโค้ดนี้
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(0,1,101)
z = 1+3*x-7*x**2+5*x**3+0.1*np.random.randn(101)
plt.scatter(x,z)
plt.show()
import matplotlib.pyplot as plt
x = np.linspace(0,1,101)
z = 1+3*x-7*x**2+5*x**3+0.1*np.random.randn(101)
plt.scatter(x,z)
plt.show()
ซึ่งดูจากตรงนี้จะเห็นว่าคำตอบที่ควรจะเป็นก็คือ w0=5, w1=21, w2=31 และ w3=1
เช่นเคย คราวนี้เราก็จะมาดูว่าวิธีการที่เราใช้จะสามารถหาคำตอบได้ตามนี้หรือเปล่า
ก่อนอื่นที่น่าพูดถึงคือวิธีการสร้างข้อมูลตัวแปรต้น โดยเดิมทีเรามีแค่ x ตัวเดียว แต่ว่าต้องสร้างค่า x ที่ยกกำลังต่างๆตั้งแต่ 0 ไปจนถึงดีกรีที่ต้องการ
อาจใช้วิธีการดังนี้
deg = 3 # ดีกรีที่ต้องการ
X = np.stack([x**i for i in range(deg+1)],1)
print(X[::20])
X = np.stack([x**i for i in range(deg+1)],1)
print(X[::20])
ได้
[[ 1. 0. 0. 0. ]
[ 1. 0.2 0.04 0.008]
[ 1. 0.4 0.16 0.064]
[ 1. 0.6 0.36 0.216]
[ 1. 0.8 0.64 0.512]
[ 1. 1. 1. 1. ]]
[ 1. 0.2 0.04 0.008]
[ 1. 0.4 0.16 0.064]
[ 1. 0.6 0.36 0.216]
[ 1. 0.8 0.64 0.512]
[ 1. 1. 1. 1. ]]
หลักแรกคือพจน์ x0 ซึ่งจะไปคูณกับ w0 จะเป็น 1 ทั้งหมด ปกติแล้ว w0 คือไบแอสซึ่งไม่ต้องการนำไปคูณกับค่า x ตัวใดๆ แต่ในที่นี้เราสร้างแถว x0 ออกมาด้วย แทนที่จะแยกค่าไบแอสออกมา
ใช้วิธีการนี้เราสามารถเขียนคลาสสำหรับการวิเคราะห์การถดถอยพหุนามแบบตัวแปรเดียวได้ดังนี้
class ThotthoiPhahunam1D:
def __init__(self,eta,deg=2):
self.eta = eta
self.deg = deg
def rianru(self,x,z,d_yut=1e-7,n_thamsam=100000):
X = np.stack([x**i for i in range(self.deg+1)],1) # ทำให้เป็นพหุนาม
self.w = np.zeros(X.shape[1])
dw = np.zeros(X.shape[1])
h = np.dot(X,self.w)
self.sse = [self.ha_sse(h,z)]
for i in range(n_thamsam):
eee = 2*(z-h)*self.eta
dw = np.dot(eee,X)
self.w += dw
h = np.dot(X,self.w)
self.sse += [self.ha_sse(h,z)]
if(np.all(np.abs(dw)<d_yut)):
break
def thamnai(self,x):
X = np.stack([x**i for i in range(self.deg+1)],1)
return np.dot(X,self.w)
def ha_sse(self,h,z):
return ((h-z)**2).sum()
def __init__(self,eta,deg=2):
self.eta = eta
self.deg = deg
def rianru(self,x,z,d_yut=1e-7,n_thamsam=100000):
X = np.stack([x**i for i in range(self.deg+1)],1) # ทำให้เป็นพหุนาม
self.w = np.zeros(X.shape[1])
dw = np.zeros(X.shape[1])
h = np.dot(X,self.w)
self.sse = [self.ha_sse(h,z)]
for i in range(n_thamsam):
eee = 2*(z-h)*self.eta
dw = np.dot(eee,X)
self.w += dw
h = np.dot(X,self.w)
self.sse += [self.ha_sse(h,z)]
if(np.all(np.abs(dw)<d_yut)):
break
def thamnai(self,x):
X = np.stack([x**i for i in range(self.deg+1)],1)
return np.dot(X,self.w)
def ha_sse(self,h,z):
return ((h-z)**2).sum()
โดยในนี้เราให้กำหนดค่าดีกรีในพารามิเตอร์ deg ตอนที่สร้างออบเจ็กต์พร้อมกับค่าอัตราการเรียนรู้
เวลาป้อนค่าตัวแปรต้นก็ใส่ค่า x ซึ่งเป็นอาเรย์มิติเดียวไป แล้วก็จะถูกแปลงเป็นพหุนามเพื่อทำการเรียนรู้ต่อไป
ลองนำมาใช้กับค่า x และ z ของโจทย์ข้อนี้ที่เราเตรียมเอาไว้ โดยสร้างออบเจ็กต์จากนั้นใช้เมธอด rianru
eta = 0.005
deg = 3
tp = ThotthoiPhahunam1D(eta,deg)
tp.rianru(x,z)
deg = 3
tp = ThotthoiPhahunam1D(eta,deg)
tp.rianru(x,z)
จากนั้นลองดูค่าน้ำหนักที่ได้
print(tp.w)
ก็จะได้ค่าน้ำหนักใกล้เคียงกับที่เราใส่ตอนสร้างข้อมูลขึ้น
[ 1.06250237 2.51213577 -5.8278461 4.21149162]
ทีนี้ลองวาดกราฟดูเทียบกับจุดข้อมูลที่ใช้เรียนรู้ โดยใช้เมธอด thamnai เพื่อหาค่าที่ทำนายโดยใช้ค่าน้ำหนักที่ได้
plt.scatter(x,z)
x = np.linspace(0,1,101)
h = tp.thamnai(x)
plt.plot(x,h,'b')
plt.show()
x = np.linspace(0,1,101)
h = tp.thamnai(x)
plt.plot(x,h,'b')
plt.show()

เส้นที่ทำนายขึ้นลากผ่านกลางจุดข้อมูลอย่างสวยงาม แสดงให้เห็นว่าการคำนวณถูกต้อง
ต่อมาลองคิดกรณีที่ปัญหาประกอบด้วย ๒ ตัวแปรต้นขึ้นไป ซึ่งจะซับซ้อนไปอีก
เช่นลองกรณีของสองมิติดังตัวอย่างนี้
x = np.random.uniform(0,4,500)
y = np.random.uniform(0,4,500)
z = 22 + 4*x + 7*y + x*x - 6*x*y + y*y + np.random.randn(500)
y = np.random.uniform(0,4,500)
z = 22 + 4*x + 7*y + x*x - 6*x*y + y*y + np.random.randn(500)
ซึ่งประกอบด้วย ๖ พจน์ คือ 1,x,y,xx,xy,yy ตามลำดับ
กรณีแบบนี้เรียกว่าเป็นพหุนามดีกรี ๒ คือผลรวมเลขชี้กำลังสูงสุดไม่เกิน ๒ ถ้ามี x*x*x หรือ x*y*y อยู่ด้วยก็จะเป็นดีกรี ๓ เป็นต้น
ลองนำมาวาดภาพการกระจายในสามมิติดู
from mpl_toolkits.mplot3d import Axes3D
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[0,4],ylim=[0,4],zlim=[z.min(),z.max()])
for i in range(len(z)):
ax.plot([x[i],x[i]],[y[i],y[i]],[z[i],0],c=plt.get_cmap('jet')((z[i]-z.min())/(z.max()-z.min())),alpha=0.2)
ax.scatter(x,y,z,c=z,edgecolor='k')
plt.show()
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[0,4],ylim=[0,4],zlim=[z.min(),z.max()])
for i in range(len(z)):
ax.plot([x[i],x[i]],[y[i],y[i]],[z[i],0],c=plt.get_cmap('jet')((z[i]-z.min())/(z.max()-z.min())),alpha=0.2)
ax.scatter(x,y,z,c=z,edgecolor='k')
plt.show()

วิธีการสร้างตัวแปรต้นสำหรับมาใช้วิเคราะห์ถดถอยพหุนามนั้น สำหรับกรณีสองตัวแปรเราอาจเขียนแจกแจงพหุนามได้ดังนี้
deg = 2
xy_ = np.stack([x**(k-i)*y**i for k in range(deg+1) for i in range(k+1)],1)
print(xy_)
xy_ = np.stack([x**(k-i)*y**i for k in range(deg+1) for i in range(k+1)],1)
print(xy_)
***ใครงงกับรูปแบบการเขียนโค้ดตรงนี้อาจลองอ่านทวนเนื้อหา ไพธอนเบื้องต้น บทที่ ๙: การทำซ้ำด้วย for ตรงส่วนของการใช้ for ซ้อน for
ได้
[[ 1.00000000e+00 2.99032562e+00 1.22752793e+00 8.94204731e+00
3.67070821e+00 1.50682481e+00]
[ 1.00000000e+00 1.51777983e+00 2.29233098e+00 2.30365561e+00
3.47925373e+00 5.25478133e+00]
[ 1.00000000e+00 9.15271919e-01 1.12181126e-01 8.37722686e-01
1.02676235e-01 1.25846051e-02]
...,
[ 1.00000000e+00 1.39509132e+00 2.08564151e+00 1.94627979e+00
2.90966036e+00 4.34990050e+00]
[ 1.00000000e+00 3.75774494e+00 2.03009611e+00 1.41206470e+01
7.62858336e+00 4.12129020e+00]
[ 1.00000000e+00 1.40287884e-02 7.70100843e-01 1.96806904e-04
1.08035818e-02 5.93055309e-01]]
3.67070821e+00 1.50682481e+00]
[ 1.00000000e+00 1.51777983e+00 2.29233098e+00 2.30365561e+00
3.47925373e+00 5.25478133e+00]
[ 1.00000000e+00 9.15271919e-01 1.12181126e-01 8.37722686e-01
1.02676235e-01 1.25846051e-02]
...,
[ 1.00000000e+00 1.39509132e+00 2.08564151e+00 1.94627979e+00
2.90966036e+00 4.34990050e+00]
[ 1.00000000e+00 3.75774494e+00 2.03009611e+00 1.41206470e+01
7.62858336e+00 4.12129020e+00]
[ 1.00000000e+00 1.40287884e-02 7.70100843e-01 1.96806904e-04
1.08035818e-02 5.93055309e-01]]
โดยกรณีนี้เป็นดีกรี ๒ ค่าที่ได้แต่ละหลักจะเป็นพจน์ของ 1,x,y,xx,xy,yy ตามลำดับ
และถ้าหากเป็นดีกรี ๓ ก็จะมีพจน์ xxx,xxy,xyy,yyy เพิ่มเข้ามาอีก รวมเป็น ๑๐ หลัก เป็นต้น
การเขียนแบบนี้ดูแล้วยุ่งยากพอสมควร อีกทั้งถ้ามี ๓ ตัวแปรการเขียนก็จะยิ่งยุ่งยากขึ้นไปอีก
พอเป็นแบบนั้นแล้วลองหาตัวช่วยเพิ่มเติมอาจจะดีกว่า เช่น หากใช้ sklearn เข้าช่วยก็อาจสามารถทำได้ง่ายขึ้น
ในมอดูลย่อย preprocessing ของ sklearn มีคลาสที่ชื่อ PolynomialFeatures อยู่ มีไว้สำหรับทำในสิ่งเดียวกับที่เราเพิ่งทำไป
ขออธิบายด้วยการยกตัวอย่างการใช้งานจริงก่อน
การใช้ลองเขียนตามนี้
from sklearn.preprocessing import PolynomialFeatures as Pf
xy = np.stack([x,y],1)
xy_ = Pf(deg).fit_transform(xy)
xy = np.stack([x,y],1)
xy_ = Pf(deg).fit_transform(xy)
ก็จะได้ xy_ แบบเดียวกับที่ใช้วิธีอย่างในตอนแรก
การใช้ PolynomialFeatures จะคล้ายกับ StandardScaler ที่กล่าวถึงไปในเรื่องของการทำข้อมูลให้เป็นมาตรฐาน https://phyblas.hinaboshi.com/20161124
คือจะใช้เมธอด fit_transform ในลักษณะเดียวกัน นั่นคือเป็นการย่อขั้นตอนการใช้ เพื่อให้ไม่ต้องใช้ fit แล้วต่อด้วย transform อีกที หากเขียนแบบเต็มๆน่าจะเป็นแบบนี้
pf = Pf(deg)
pf.fit(xy)
xy_ = pf.transform(xy)
pf.fit(xy)
xy_ = pf.transform(xy)
เมื่อใช้ PolynomialFeatures แบบนี้แล้วจะใช้กับปัญหาที่มีตัวแปรต้นกี่ตัวก็ได้ เช่นถ้าลองใช้กับ ๓ ตัวแปรดู แจกแจงถึงดีกรี ๒
x1 = np.linspace(0,2,3)
x2 = np.linspace(0,3,3)
x3 = np.linspace(0,5,3)
print(Pf(2).fit_transform(np.stack([x1,x2,x3],1)))
x2 = np.linspace(0,3,3)
x3 = np.linspace(0,5,3)
print(Pf(2).fit_transform(np.stack([x1,x2,x3],1)))
ได้
[[ 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]
[ 1. 1. 1.5 2.5 1. 1.5 2.5 2.25 3.75 6.25]
[ 1. 2. 3. 5. 4. 6. 10. 9. 15. 25. ]]
[ 1. 1. 1.5 2.5 1. 1.5 2.5 2.25 3.75 6.25]
[ 1. 2. 3. 5. 4. 6. 10. 9. 15. 25. ]]
ผลที่ได้มี ๑๐ พจน์ ตามนี้ 1, x1, x2, x3, x1x1, x1x2, x1x3, x2x2, x2x3, x3x3
เมื่อเข้าใจวิธีการแปลงตัวแปรต้นให้เป็นพหุนามแล้ว ก็ลองสร้างแบบจำลองขึ้นดู เขียนได้ดังนี้
import numpy as np
from sklearn.preprocessing import PolynomialFeatures as Pf
class ThotthoiPhahunam:
def __init__(self,eta,deg=2):
self.eta = eta
self.deg = deg
def rianru(self,X,z,d_yut=1e-7,n_thamsam=100000):
X = Pf(self.deg).fit_transform(X)
self.w = np.zeros(X.shape[1])
dw = np.zeros(X.shape[1])
h = np.dot(X,self.w)
self.sse = [self.ha_sse(h,z)]
for i in range(n_thamsam):
eee = 2*(z-h)*self.eta
dw = np.dot(eee,X)
self.w += dw
h = np.dot(X,self.w)
self.sse += [self.ha_sse(h,z)]
if(np.all(np.abs(dw)<d_yut)):
break
def thamnai(self,X):
X = Pf().fit_transform(X)
return np.dot(X,self.w)
def ha_sse(self,h,z):
return ((h-z)**2).sum()
from sklearn.preprocessing import PolynomialFeatures as Pf
class ThotthoiPhahunam:
def __init__(self,eta,deg=2):
self.eta = eta
self.deg = deg
def rianru(self,X,z,d_yut=1e-7,n_thamsam=100000):
X = Pf(self.deg).fit_transform(X)
self.w = np.zeros(X.shape[1])
dw = np.zeros(X.shape[1])
h = np.dot(X,self.w)
self.sse = [self.ha_sse(h,z)]
for i in range(n_thamsam):
eee = 2*(z-h)*self.eta
dw = np.dot(eee,X)
self.w += dw
h = np.dot(X,self.w)
self.sse += [self.ha_sse(h,z)]
if(np.all(np.abs(dw)<d_yut)):
break
def thamnai(self,X):
X = Pf().fit_transform(X)
return np.dot(X,self.w)
def ha_sse(self,h,z):
return ((h-z)**2).sum()
ลักษณะคล้ายกับกรณีตัวแปรเดียวแต่ว่าค่า X ที่ต้องใส่ตอนที่เรียนรู้คราวนี้เป็นอาเรย์สองมิติ และใช้ PolynomialFeatures ในการทำให้เป็นพหุนาม โดยค่า deg จะกำหนดดีกรีที่ต้องการแปลง
นำมาใช้กับ x,y,z ที่เพิ่งเตรียมไว้จากตัวอย่างที่แล้ว แล้วลองวาดผลที่ได้ดู
X = np.stack([x,y],1)
eta = 0.00001
deg = 2
tp = ThotthoiPhahunam(eta,deg)
tp.rianru(X,z)
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[0,4],ylim=[0,4],zlim=[z.min(),z.max()])
mx,my = np.meshgrid(np.linspace(0,4,11),np.linspace(0,4,11))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = tp.thamnai(mX).reshape(11,11)
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2,color='b',edgecolor='k')
h = tp.thamnai(X)
for i in range(len(z)):
ax.plot([x[i],x[i]],[y[i],y[i]],[h[i],z[i]],'k')
ax.scatter(x,y,z,c=np.abs(z-h),edgecolor='k',cmap='jet')
plt.show()
eta = 0.00001
deg = 2
tp = ThotthoiPhahunam(eta,deg)
tp.rianru(X,z)
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[0,4],ylim=[0,4],zlim=[z.min(),z.max()])
mx,my = np.meshgrid(np.linspace(0,4,11),np.linspace(0,4,11))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = tp.thamnai(mX).reshape(11,11)
ax.plot_surface(mx,my,mz,rstride=1,cstride=1,alpha=0.2,color='b',edgecolor='k')
h = tp.thamnai(X)
for i in range(len(z)):
ax.plot([x[i],x[i]],[y[i],y[i]],[h[i],z[i]],'k')
ax.scatter(x,y,z,c=np.abs(z-h),edgecolor='k',cmap='jet')
plt.show()

พื้นผิวค่าที่ได้ลากผ่านกลางระหว่างจุดแสดงว่าแทนคำตอบได้ดี
ลองดูค่าน้ำหนักที่ได้
print(tp.w)
ได้ค่าออกมาใกล้เคียงกับ [22,4,7,1,-6,1] ซึ่งเป็นคำตอบที่ควรเป็นจริงๆ
[ 21.89569089 4.39975668 6.65906795 0.91058478 -6.01294355
1.08767486]
1.08767486]
อ้างอิง
http://tkengo.github.io/blog/2016/06/02/yaruo-machine-learning3
http://techtipshoge.blogspot.com/2015/06/scikit-learn.html
http://ai-programming.hatenablog.jp/entry/2016/02/19/204649
http://blog.csdn.net/lulei1217/article/details/49582821
https://www.amazon.co.jp/Python機械学習プログラミング-達人データサイエンティストによる理論と実践-impress-top-gearシリーズ-ebook/dp/B01HGIPIAK
http://techtipshoge.blogspot.com/2015/06/scikit-learn.html
http://ai-programming.hatenablog.jp/entry/2016/02/19/204649
http://blog.csdn.net/lulei1217/article/details/49582821
https://www.amazon.co.jp/Python機械学習プログラミング-達人データサイエンティストによる理論と実践-impress-top-gearシリーズ-ebook/dp/B01HGIPIAK
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy