[python] การวิเคราะห์องค์ประกอบหลักแบบเคอร์เนล
เขียนเมื่อ 2018/07/30 18:43
แก้ไขล่าสุด 2022/07/19 05:22
ในตอนที่แล้วได้เขียนถึงการวิเคราะห์องค์ประกอบหลัก (主成分分析, principle component Analysis, PCA) ไปแล้ว https://phyblas.hinaboshi.com/20180727
สำหรับตอนนี้จะอธิบายการนำวิธีการเคอรเนลมาใช้ร่วมกับการวิเคราะห์องค์ประกอบหลัก เรียกว่าการวิเคราะห์องค์ประกอบหลักแบบเคอร์เนล (核主成分分析, kernel principal component analysis, kernel PCA)
ในการวิเคราะห์องค์ประกอบหลักแบบดั้งเดิมนั้นเป็นแค่การหมุนแกน การเปลี่ยนแปลงทั้งหมดเป็นแบบเชิงเส้น ดังนั้นไม่ว่าจะแปลงยังไง ข้อมูลก็จะยังคงมีหน้าตาเดิม ไม่เปลี่ยนแปลงไปนัก
ดังนั้นวิธีนี้จึงใช้ไม่ได้ผลกับข้อมูลที่ไม่สามารถแบ่งเป็นเชิงเส้นได้
ตัวอย่างเช่นข้อมูลรูปจันทร์เสี้ยวซึ่งเคยยกตัวอย่างไปใน https://phyblas.hinaboshi.com/20171202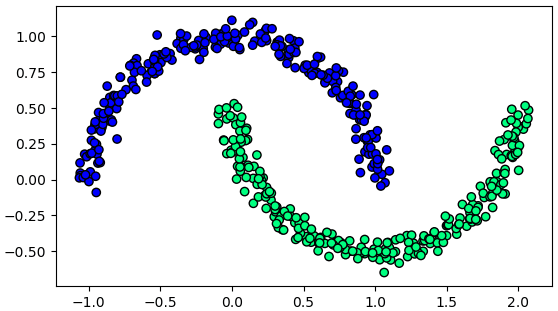
ข้อมูลแบบนี้ไม่ว่าจะหมุนแกนยังไงก็ไม่มีทางแยกข้อมูลให้อยู่ในแกนเดียวได้
แต่หากนำวิธีการเคอร์เนลมาประยุกต์ใช้กับการวิเคราะห์องค์ประกอบหลักก็จะทำให้สามารถแปลงข้อมูลแบบไม่ใช่เชิงเส้นได้
เรื่องแนวคิดพื้นฐานของวิธีการเคอร์เนลเขียนเอาไว้ใน https://phyblas.hinaboshi.com/20180724
ดังนั้นในที่นี้จะไม่พูดถึงรายละเอียดมากแต่จะหยิบมาใช้
ในการวิเคราะห์องค์ประกอบหลักแบบดั้งเดิมนั้นเราจะคำนวณความแปรปรวนร่วมเกี่ยวของจุดข้อมูลต่างๆโดยพิจารณาแต่ละมิติ คือ
..(1)
โดย i และ j เป็นดัชนีมิติของข้อมูล ส่วน k คือดัชนีลำดับข้อมูล โดยมีข้อมูลอยู่ n ตัว
หรือเขียนในรูปผลคูณภายในได้เป็น
..(2)
โดยในที่นี้เวกเตอร์ของ x หมายถึงค่าในมิตินึงของข้อมูลทั้งหมด
..(3)
แต่ในการวิเคราะห์องค์ประกอบหลักแบบเคอร์เนลจะเปลี่ยนแนวทางในการพิจารณาใหม่ คือจะคำนวณความแปรปรวนร่วมเกี่ยวของฟังก์ชันฐานต่างๆโดยพิจารณาแต่ละจุดข้อมูล
..(4)
ในที่นี้ i และ j เป็นดัชนีลำดับข้อมูล ส่วน k คือดัชนีลำดับของฟังก์ชันฐาน และเวกเตอร์ x ในที่นี้คือค่าของข้อมูลตัวนึงในทุกมิติ
..(5)
เมื่ออาศัยความรู้เรื่องวิธีการเคอร์เนลแล้ว จะรู้ว่าผลคูณภายในของฟังก์ชันฐานสามารถเขียนแทนในรูปของเคอร์เนลได้
..(6)
ดังนั้นการคำนวณความแปรปรวนร่วมเกี่ยวก็คือการคำนวณเคอร์เนลนั่นเอง ในที่นี้จึงใช้เคอร์เนลในทำนองเดียวกับที่เคยพิจารณาความแปรปรวนร่วมเกี่ยว
ส่วนเวลาคำนวณเพื่อเปลี่ยนพิกัดนั้น หากเป็นการวิเคราะห์องค์ประกอบแบบดั้งเดิมจะคำนวณโดยเอาค่าเดิมมาคูณกับเวกเตอร์ลักษณะเฉพาะ
..(7)
แต่ว่าเมื่อใช้เคอร์เนล จะเปลี่ยนเป็นคำนวณจากเคอร์เนลแทน แบบนี้
..(8)
โดย
..(9)
..(10)
ในที่นี้ m คือจำนวนมิติของข้อมูลหลังแปลงแล้ว ซึ่งจริงๆแล้ว m ควรจะมีจำนวนเท่ากับจำนวนข้อมูล นั่นคือ m=n เพียงแต่ถ้าเป็นแบบนั้นเท่ากับเป็นการเพิ่มมิติ โดยทั่วไปจะเลือกแค่ตัวที่มีค่าลักษณะเฉพาะสูงสุดอันดับต้นๆ
ส่วน x เป็นเมทริกซ์ของข้อมูลทั้งหมดในทุกมิติ
..(11)
ให้เมทริกซ์ x' เป็นเมทริกซ์ของข้อมูลชุดใหม่ และ ξ(x') เป็นเมทริกซ์ของข้อมูลใหม่หลังแปลง
..(12)
ค่าหลังแปลงจะคำนวณได้จาก
..(13)
โดย K เป็นเมทริกซ์ของเคอร์เนลที่คำนวนระหว่างข้อมูลใหม่กับข้อมูลที่ใช้เรียนรู้
..(14)
ค่าหลังแปลงแล้วจะคำนวณได้เป็น
..(15)
ทีนี้ เช่นเดียวกับตอนที่ทำการวิเคราะห์องค์ประกอบแบบดั้งเดิม เราสามารถตั้งสมการปัญหาเวกเตอร์ลักษณะเฉพาะได้
..(16)
โดย K(x,x) คือเคอร์เนลที่คำนวณภายในชุดข้อมูลที่ใช้ในการเรียนรู้
ส่วน Λ คือเมทริกซ์ของค่าลักษณะเฉพาะ
..(17)
และ V* คือ เมทริกซ์ของเวกเตอร์ลักษณะเฉพาะ
ในที่นี้ทำการคำนวณหาเวกเตอร์และค่าลักษณะเฉพาะของ K(x,x) ก็จะได้ Λ และ V* ออกมา การคำนวณหาค่าตรงนี้ใช้ np.linalg.eigh ได้เช่นเดียวกัน
จากนั้นเมทริกซ์ V จากสมการ (13) ก็คำนวณได้จาก
..(18)
แล้วจึงได้ว่า
..(19)
สำหรับ ξ ของ x ที่เป็นข้อมูลที่ใช้เรียนรู้นั้นจะได้ว่า
..(20)
นั่นคือตัวเวกเตอร์ลักษณะเฉพาะที่หาค่าได้จะเป็นค่าหลังแปลงของข้อมูลที่ใช้เรียนรู้ไปโดยทันที ดังนั้นถ้าแค่จะคำนวณเพื่อหาในพิกัดใหม่ของข้อมูลที่ใช้เรียนรู้ละก็ แค่หาเวกเตอร์ลักษณะเฉพาะได้ก็จบเลย แต่ถ้าต้องการหาชุดข้อมูลใหม่ก็ต้องคำนวณเคอร์เนลใหม่แล้วก็นำไปคูณตามสมการ (19)
ส่วนสำคัญที่ต้องเสริมอีกคือ K ในที่นี้ไม่ใช่เคอร์เนลที่คำนวณจากฟังก์ชันเคอร์เนลธรรมดา แต่ต้องมีการปรับเข้าศูนย์กลาง (中心化, centering)
ให้ K* เป็นค่าที่ได้จากการคำนวณโดยเคอร์เนลฟังก์ชันธรรมดา ยังไม่ได้ปรับเข้าศูนย์กลาง จะคำนวณค่า K ที่ได้หลังจากปรับเข้าศูนย์กลางได้ดังนี้
..(21)
เมทริกซ์ของเคอร์เนลที่ปรับเข้าศูนย์กลางแล้วสามารถคำนวณได้เป็น
..(22)
โดย 1n คือเมทริกซ์ที่ค่าของทุกตัวเป็น 1/n
ในไพธอนอาจเขียนโค้ดได้ในลักษณะนี้
อย่างไรก็ตาม สามารถคำนวณในลักษณะเดียวกันนี้ได้โดยใช้ KernelCenterer ของ sklearn ซึ่งจะได้ผลเหมือนกันแต่เร็วขึ้นมาก
โดยรวมแล้ว ข้อแตกต่างที่สำคัญระหว่างการวิเคราะห์องค์ประกอบหลักแบบใช้เคอร์เนลกับไม่ใช้ก็คือ สิ่งที่พิจารณาในแบบเคอร์เนลจะไม่ใช่ความแปรปรวนระหว่างแต่ละมิติ แต่เป็นความแปรปรวนระหว่างฟังก์ชันฐาน และเวกเตอร์ลักษณะเฉพาะและค่าลักษณะเฉพาะจะมีจำนวนเท่ากับจำนวนข้อมูล แทนที่จะเป็นจำนวนมิติ
โปรแกรม
ลองนำวิธีการมาใช้กับข้อมูลรูปพระจันทร์เสี้ยวที่ยกเป็นตัวอย่างมาข้างต้น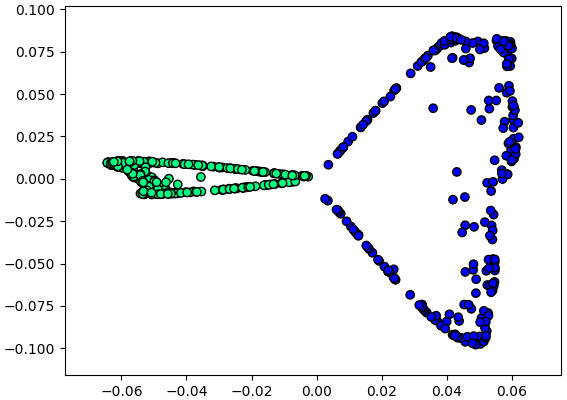
ผลที่ได้จะเห็นว่าข้อมูลทั้งสองกลุ่มถูกแยกตามแกนนอนได้ ซึ่งทำให้สามารถลดปัญหาเหลือมิติเดียวได้
เมื่อต้องการแปลงพิกัดของข้อมูลชุดอื่นที่ไม่ได้ถูกรวมอยู่ในชุดที่ใช้ตอนแรกก็คำนวณเคอร์เนลแล้วคูณกับ V
เพื่อให้แน่ใจว่าตำแหน่งถูกต้อง ลองให้ข้อมูลใหม่มาจากข้อมูลเก่าส่วนหนึ่ง คำนวณตำแหน่งจุดใหม่วาดซ้อนลงไป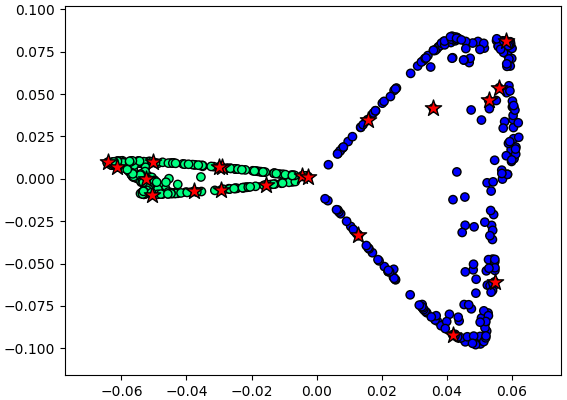
ตำแหน่งที่ได้ตรงกันดี แสดงว่าการคำนวณเป็นไปตามที่ควรจะเป็น
เขียนเป็นคลาส
ต่อมาลองเรียบเรียงเขียนใหม่ในรูปแบบคลาส
เนื่องจากเวกเตอร์ลักษณะเฉพาะที่คำนวณได้ก็คือค่าในพิกัดใหม่ของข้อมูลที่ใช้เรียนรู้อยู่แล้ว ดังนั้นจึงให้คืนค่านั้นกลับไปในขั้นตอนการเรียนรู้เลย
ลองทดสอบกับข้อมูลไวน์ (https://phyblas.hinaboshi.com/20171207)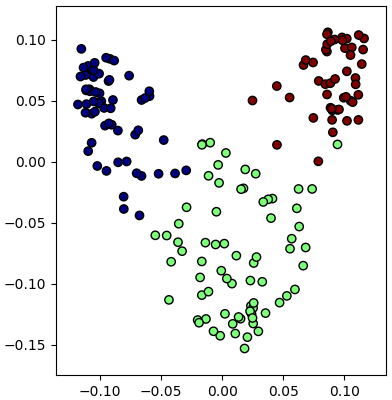
หากเทียบกับตอนใช้การวิเคราะห์องค์ประกอบแบบเชิงเส้นธรรมดา ผลที่ได้จะดูออกมาดีกว่า
เพียงแต่ว่าการเลือกค่า γ ให้เหมาะสมเป็นเรื่องที่สำคัญ เพราะมีผลต่อผลลัพธ์ที่จะได้มาก
เปรียบเทียบผลของค่า γ
ลองใช้ข้อมูลกลุ่มรูปไข่ดาวเป็นตัวอย่างเพื่อเปรียบเทียบผลของค่า γ ที่ต่างกัน (รายละเอียดเกี่ยวกับชุดข้อมูลนี้ https://phyblas.hinaboshi.com/20180716)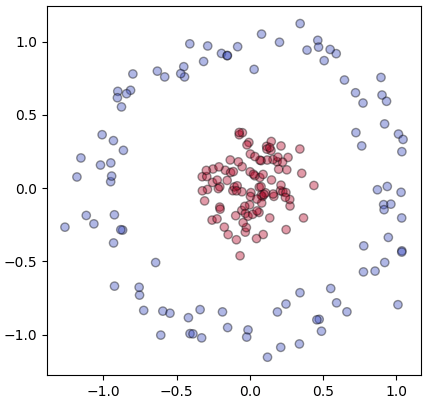
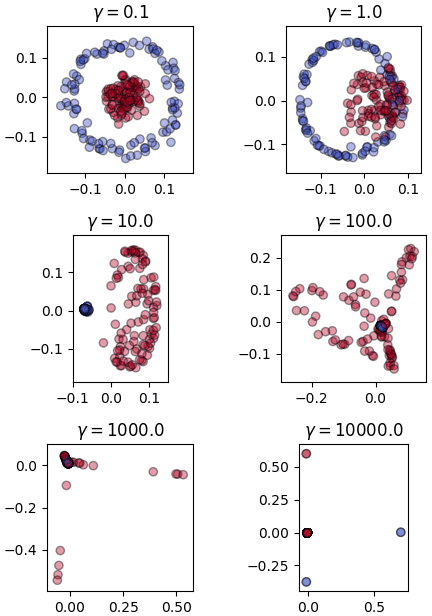
จะเห็นว่าผลที่ได้ต่างกันออกไปมาก จึงควรเลือกค่า γ ให้เหมาะสม
อ้างอิง
สำหรับตอนนี้จะอธิบายการนำวิธีการเคอรเนลมาใช้ร่วมกับการวิเคราะห์องค์ประกอบหลัก เรียกว่าการวิเคราะห์องค์ประกอบหลักแบบเคอร์เนล (核主成分分析, kernel principal component analysis, kernel PCA)
ในการวิเคราะห์องค์ประกอบหลักแบบดั้งเดิมนั้นเป็นแค่การหมุนแกน การเปลี่ยนแปลงทั้งหมดเป็นแบบเชิงเส้น ดังนั้นไม่ว่าจะแปลงยังไง ข้อมูลก็จะยังคงมีหน้าตาเดิม ไม่เปลี่ยนแปลงไปนัก
ดังนั้นวิธีนี้จึงใช้ไม่ได้ผลกับข้อมูลที่ไม่สามารถแบ่งเป็นเชิงเส้นได้
ตัวอย่างเช่นข้อมูลรูปจันทร์เสี้ยวซึ่งเคยยกตัวอย่างไปใน https://phyblas.hinaboshi.com/20171202
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
X,z = datasets.make_moons(500,noise=0.05,random_state=0)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='winter')
plt.show()
ข้อมูลแบบนี้ไม่ว่าจะหมุนแกนยังไงก็ไม่มีทางแยกข้อมูลให้อยู่ในแกนเดียวได้
แต่หากนำวิธีการเคอร์เนลมาประยุกต์ใช้กับการวิเคราะห์องค์ประกอบหลักก็จะทำให้สามารถแปลงข้อมูลแบบไม่ใช่เชิงเส้นได้
เรื่องแนวคิดพื้นฐานของวิธีการเคอร์เนลเขียนเอาไว้ใน https://phyblas.hinaboshi.com/20180724
ดังนั้นในที่นี้จะไม่พูดถึงรายละเอียดมากแต่จะหยิบมาใช้
ในการวิเคราะห์องค์ประกอบหลักแบบดั้งเดิมนั้นเราจะคำนวณความแปรปรวนร่วมเกี่ยวของจุดข้อมูลต่างๆโดยพิจารณาแต่ละมิติ คือ
..(1)
โดย i และ j เป็นดัชนีมิติของข้อมูล ส่วน k คือดัชนีลำดับข้อมูล โดยมีข้อมูลอยู่ n ตัว
หรือเขียนในรูปผลคูณภายในได้เป็น
..(2)
โดยในที่นี้เวกเตอร์ของ x หมายถึงค่าในมิตินึงของข้อมูลทั้งหมด
..(3)
แต่ในการวิเคราะห์องค์ประกอบหลักแบบเคอร์เนลจะเปลี่ยนแนวทางในการพิจารณาใหม่ คือจะคำนวณความแปรปรวนร่วมเกี่ยวของฟังก์ชันฐานต่างๆโดยพิจารณาแต่ละจุดข้อมูล
..(4)
ในที่นี้ i และ j เป็นดัชนีลำดับข้อมูล ส่วน k คือดัชนีลำดับของฟังก์ชันฐาน และเวกเตอร์ x ในที่นี้คือค่าของข้อมูลตัวนึงในทุกมิติ
..(5)
เมื่ออาศัยความรู้เรื่องวิธีการเคอร์เนลแล้ว จะรู้ว่าผลคูณภายในของฟังก์ชันฐานสามารถเขียนแทนในรูปของเคอร์เนลได้
..(6)
ดังนั้นการคำนวณความแปรปรวนร่วมเกี่ยวก็คือการคำนวณเคอร์เนลนั่นเอง ในที่นี้จึงใช้เคอร์เนลในทำนองเดียวกับที่เคยพิจารณาความแปรปรวนร่วมเกี่ยว
ส่วนเวลาคำนวณเพื่อเปลี่ยนพิกัดนั้น หากเป็นการวิเคราะห์องค์ประกอบแบบดั้งเดิมจะคำนวณโดยเอาค่าเดิมมาคูณกับเวกเตอร์ลักษณะเฉพาะ
..(7)
แต่ว่าเมื่อใช้เคอร์เนล จะเปลี่ยนเป็นคำนวณจากเคอร์เนลแทน แบบนี้
..(8)
โดย
..(9)
..(10)
ในที่นี้ m คือจำนวนมิติของข้อมูลหลังแปลงแล้ว ซึ่งจริงๆแล้ว m ควรจะมีจำนวนเท่ากับจำนวนข้อมูล นั่นคือ m=n เพียงแต่ถ้าเป็นแบบนั้นเท่ากับเป็นการเพิ่มมิติ โดยทั่วไปจะเลือกแค่ตัวที่มีค่าลักษณะเฉพาะสูงสุดอันดับต้นๆ
ส่วน x เป็นเมทริกซ์ของข้อมูลทั้งหมดในทุกมิติ
..(11)
ให้เมทริกซ์ x' เป็นเมทริกซ์ของข้อมูลชุดใหม่ และ ξ(x') เป็นเมทริกซ์ของข้อมูลใหม่หลังแปลง
..(12)
ค่าหลังแปลงจะคำนวณได้จาก
..(13)
โดย K เป็นเมทริกซ์ของเคอร์เนลที่คำนวนระหว่างข้อมูลใหม่กับข้อมูลที่ใช้เรียนรู้
..(14)
ค่าหลังแปลงแล้วจะคำนวณได้เป็น
..(15)
ทีนี้ เช่นเดียวกับตอนที่ทำการวิเคราะห์องค์ประกอบแบบดั้งเดิม เราสามารถตั้งสมการปัญหาเวกเตอร์ลักษณะเฉพาะได้
..(16)
โดย K(x,x) คือเคอร์เนลที่คำนวณภายในชุดข้อมูลที่ใช้ในการเรียนรู้
ส่วน Λ คือเมทริกซ์ของค่าลักษณะเฉพาะ
..(17)
และ V* คือ เมทริกซ์ของเวกเตอร์ลักษณะเฉพาะ
ในที่นี้ทำการคำนวณหาเวกเตอร์และค่าลักษณะเฉพาะของ K(x,x) ก็จะได้ Λ และ V* ออกมา การคำนวณหาค่าตรงนี้ใช้ np.linalg.eigh ได้เช่นเดียวกัน
จากนั้นเมทริกซ์ V จากสมการ (13) ก็คำนวณได้จาก
..(18)
แล้วจึงได้ว่า
..(19)
สำหรับ ξ ของ x ที่เป็นข้อมูลที่ใช้เรียนรู้นั้นจะได้ว่า
..(20)
นั่นคือตัวเวกเตอร์ลักษณะเฉพาะที่หาค่าได้จะเป็นค่าหลังแปลงของข้อมูลที่ใช้เรียนรู้ไปโดยทันที ดังนั้นถ้าแค่จะคำนวณเพื่อหาในพิกัดใหม่ของข้อมูลที่ใช้เรียนรู้ละก็ แค่หาเวกเตอร์ลักษณะเฉพาะได้ก็จบเลย แต่ถ้าต้องการหาชุดข้อมูลใหม่ก็ต้องคำนวณเคอร์เนลใหม่แล้วก็นำไปคูณตามสมการ (19)
ส่วนสำคัญที่ต้องเสริมอีกคือ K ในที่นี้ไม่ใช่เคอร์เนลที่คำนวณจากฟังก์ชันเคอร์เนลธรรมดา แต่ต้องมีการปรับเข้าศูนย์กลาง (中心化, centering)
ให้ K* เป็นค่าที่ได้จากการคำนวณโดยเคอร์เนลฟังก์ชันธรรมดา ยังไม่ได้ปรับเข้าศูนย์กลาง จะคำนวณค่า K ที่ได้หลังจากปรับเข้าศูนย์กลางได้ดังนี้
..(21)
เมทริกซ์ของเคอร์เนลที่ปรับเข้าศูนย์กลางแล้วสามารถคำนวณได้เป็น
..(22)
โดย 1n คือเมทริกซ์ที่ค่าของทุกตัวเป็น 1/n
ในไพธอนอาจเขียนโค้ดได้ในลักษณะนี้
n = K.shape[0]
_1n = np.ones((n,n))/n
_1nK = _1n.dot(K)
K = K - _1nK - K.dot(_1n) + _1nK.dot(_1n)อย่างไรก็ตาม สามารถคำนวณในลักษณะเดียวกันนี้ได้โดยใช้ KernelCenterer ของ sklearn ซึ่งจะได้ผลเหมือนกันแต่เร็วขึ้นมาก
from sklearn.preprocessing import KernelCenterer
kc = KernelCenterer()
K = kc.fit_transform(K)โดยรวมแล้ว ข้อแตกต่างที่สำคัญระหว่างการวิเคราะห์องค์ประกอบหลักแบบใช้เคอร์เนลกับไม่ใช้ก็คือ สิ่งที่พิจารณาในแบบเคอร์เนลจะไม่ใช่ความแปรปรวนระหว่างแต่ละมิติ แต่เป็นความแปรปรวนระหว่างฟังก์ชันฐาน และเวกเตอร์ลักษณะเฉพาะและค่าลักษณะเฉพาะจะมีจำนวนเท่ากับจำนวนข้อมูล แทนที่จะเป็นจำนวนมิติ
โปรแกรม
ลองนำวิธีการมาใช้กับข้อมูลรูปพระจันทร์เสี้ยวที่ยกเป็นตัวอย่างมาข้างต้น
from sklearn.preprocessing import KernelCenterer
from scipy.spatial.distance import cdist
def gauss(X1,X2):
return np.exp(-gamma*cdist(X1,X2,'sqeuclidean'))
X,z = datasets.make_moons(500,noise=0.05,random_state=0)
gamma = 20
K = gauss(X,X)
kc = KernelCenterer()
K = kc.fit_transform(K) # ปรับเข้าศูนย์กลาง
kha_eig,vec_eig = np.linalg.eigh(K)
Xi = vec_eig[:,::-1][:,:2]
a = kha_eig[::-1][:2]
V = Xi/a
plt.scatter(Xi[:,0],Xi[:,1],c=z,edgecolor='k',cmap='winter')
plt.show()
ผลที่ได้จะเห็นว่าข้อมูลทั้งสองกลุ่มถูกแยกตามแกนนอนได้ ซึ่งทำให้สามารถลดปัญหาเหลือมิติเดียวได้
เมื่อต้องการแปลงพิกัดของข้อมูลชุดอื่นที่ไม่ได้ถูกรวมอยู่ในชุดที่ใช้ตอนแรกก็คำนวณเคอร์เนลแล้วคูณกับ V
เพื่อให้แน่ใจว่าตำแหน่งถูกต้อง ลองให้ข้อมูลใหม่มาจากข้อมูลเก่าส่วนหนึ่ง คำนวณตำแหน่งจุดใหม่วาดซ้อนลงไป
X2,z2 = X[:20],z[:20]
# คำนวณเคอร์เนลแล้วปรับเข้าศูนย์กลางแล้วจึงคูณกับ V
Xi2 = kc.transform(gauss(X2,X)).dot(V)
plt.scatter(Xi[:,0],Xi[:,1],c=z,edgecolor='k',cmap='winter')
plt.scatter(Xi2[:,0],Xi2[:,1],150,c='r',marker='*',edgecolor='k')
plt.show()
ตำแหน่งที่ได้ตรงกันดี แสดงว่าการคำนวณเป็นไปตามที่ควรจะเป็น
เขียนเป็นคลาส
ต่อมาลองเรียบเรียงเขียนใหม่ในรูปแบบคลาส
class WikhroOngprakopLakKernel:
def __init__(self,gamma,m=None):
self.gamma = gamma
self.m = m
self.kc = KernelCenterer()
def rianru(self,X):
self.X = X
if(self.m): m = self.m
else: m = X.shape[0]
K = self.kernel(X,X)
K = self.kc.fit_transform(K)
kha_eig,vec_eig = np.linalg.eigh(K)
Xi = vec_eig[:,::-1][:,:m]
self.a = kha_eig[::-1][:m]
self.V = Xi/self.a
return Xi
def plaeng(self,X):
return self.kc(self.kernel(X,self.X)).dot(self.V)
def kernel(self,X1,X2):
return np.exp(-self.gamma*cdist(X1,X2,'sqeuclidean'))เนื่องจากเวกเตอร์ลักษณะเฉพาะที่คำนวณได้ก็คือค่าในพิกัดใหม่ของข้อมูลที่ใช้เรียนรู้อยู่แล้ว ดังนั้นจึงให้คืนค่านั้นกลับไปในขั้นตอนการเรียนรู้เลย
ลองทดสอบกับข้อมูลไวน์ (https://phyblas.hinaboshi.com/20171207)
gamma = 0.07
m = 2
w = datasets.load_wine()
X,z = w.data,w.target
X = (X-X.mean(0))/X.std(0) # แปลงข้อมูลให้เป็นมาตรฐาน
wol = WikhroOngprakopLakKernel(gamma=gamma,m=m)
Xi = wol.rianru(X)
plt.axes(aspect=1)
plt.scatter(Xi[:,0],Xi[:,1],c=z,cmap='jet',edgecolor='k')
plt.show()
plt.figure()
หากเทียบกับตอนใช้การวิเคราะห์องค์ประกอบแบบเชิงเส้นธรรมดา ผลที่ได้จะดูออกมาดีกว่า
เพียงแต่ว่าการเลือกค่า γ ให้เหมาะสมเป็นเรื่องที่สำคัญ เพราะมีผลต่อผลลัพธ์ที่จะได้มาก
เปรียบเทียบผลของค่า γ
ลองใช้ข้อมูลกลุ่มรูปไข่ดาวเป็นตัวอย่างเพื่อเปรียบเทียบผลของค่า γ ที่ต่างกัน (รายละเอียดเกี่ยวกับชุดข้อมูลนี้ https://phyblas.hinaboshi.com/20180716)
n = 200
X,z = datasets.make_circles(n,factor=0.2,noise=0.1)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,alpha=0.4,cmap='coolwarm',edgecolor='k')
plt.figure(figsize=[5,9])
for i,gamma in enumerate(np.logspace(-1,4,6)):
plt.subplot(321+i,aspect=1,title='$\\gamma=%.1f$'%gamma)
wol = WikhroOngprakopLakKernel(gamma=gamma,m=2)
Xi = wol.rianru(X)
plt.scatter(Xi[:,0],Xi[:,1],c=z,alpha=0.4,cmap='coolwarm',edgecolor='k')
plt.tight_layout()
plt.show()

จะเห็นว่าผลที่ได้ต่างกันออกไปมาก จึงควรเลือกค่า γ ให้เหมาะสม
อ้างอิง
https://www.amazon.co.jp/Python機械学習プログラミング-達人データサイエンティストによる理論と実践-impress-top-gearシリーズ-ebook/dp/B01HGIPIAK
https://qiita.com/NoriakiOshita/items/138c10eada03938fcd79
https://qiita.com/takseki/items/944be1ce92df9a4ff355
http://www.ism.ac.jp/%7Efukumizu/OsakaU2014/OsakaU_1intro.pdf
http://enakai00.hatenablog.com/entry/2016/09/09/103142
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1618-03.pdf
https://zhanxw.com/blog/2011/02/kernel-pca-%E5%8E%9F%E7%90%86%E5%92%8C%E6%BC%94%E7%A4%BA
https://blog.csdn.net/zhangping1987/article/details/30492433
https://qiita.com/NoriakiOshita/items/138c10eada03938fcd79
https://qiita.com/takseki/items/944be1ce92df9a4ff355
http://www.ism.ac.jp/%7Efukumizu/OsakaU2014/OsakaU_1intro.pdf
http://enakai00.hatenablog.com/entry/2016/09/09/103142
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1618-03.pdf
https://zhanxw.com/blog/2011/02/kernel-pca-%E5%8E%9F%E7%90%86%E5%92%8C%E6%BC%94%E7%A4%BA
https://blog.csdn.net/zhangping1987/article/details/30492433
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn