[python] ใช้ชุดข้อมูลดอกไม้เป็นตัวอย่างเพื่อทดสอบการเรียนรู้ของเครื่อง
เขียนเมื่อ 2018/08/08 00:50
แก้ไขล่าสุด 2024/10/12 09:27
ชุดข้อมูลดอกไม้ของฟิชเชอร์ เป็นชุดข้อมูลหนึ่งที่นิยมนำมาใช้เป็นตัวอย่างเพื่อฝึกหรือทดสอบปัญหาการวิเคราะห์แบ่งกลุ่มในการเรียนรู้ของเครื่องกันอย่างกว้างขวาง
ชุดข้อมูลนี้เป็นข้อมูลของดอกไม้สกุล Iris ทั้งหมด ๑๕๐ ดอกซึ่งถูกเก็บรวบรวมจากคาบสมุทรกาสเป (Gaspé) ประเทศแคนาดา โดยเอดการ์ แอนเดอร์สัน (Edgar Anderson) นักพฤกษศาสตร์ (บางครั้งจึงเรียกว่าข้อมูลดอกไม้ของแอนเดอร์สัน)
ชุดข้อมูลนี้เริ่มถูกนำมาใช้ในปี 1936 โดยรอนัลด์ ฟิชเชอร์ (Ronald Fisher) นักสถิติ โดยใช้เป็นตัวอย่างในการอธิบายการวิเคราะห์การจำแนกประเภทเชิงเส้น (线性判别分析, linear discriminant analysis)
เรื่องการวิเคราะห์การจำแนกประเภทเชิงเส้นได้เคยแนะนำไปใน https://phyblas.hinaboshi.com/20180802
ข้อมูลดอกไม้ประกอบไปด้วย
0. ความยาวกลีบเลี้ยง
1. ความกว้างกลีบเลี้ยง
2. ความยาวกลีบดอก
3. ความกว้างกลีบดอก
ดอกไม้มี ๓ สายพันธุ์ ได้แก่
0. Iris setosa
1. Iris versicolor
2. Iris virginica
ใน sklearn ได้ใส่ชุดข้อมูลนี้ไว้อยู่ในมอดูลย่อย datasets แล้ว จึงนำมาใช้ได้ง่ายในทันที
ได้
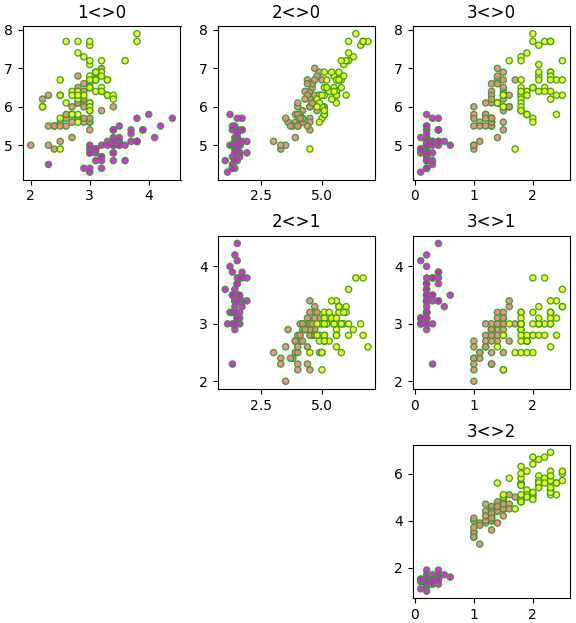
เนื่องจากข้อมูลเป็นสี่มิติ การแสดงภาพให้เห็นค่อนข้างยาก อาจลองดูการกระจายในสองมิติโดยจับคู่ดูทีละ ๒ ตัวแปร แบบนี้
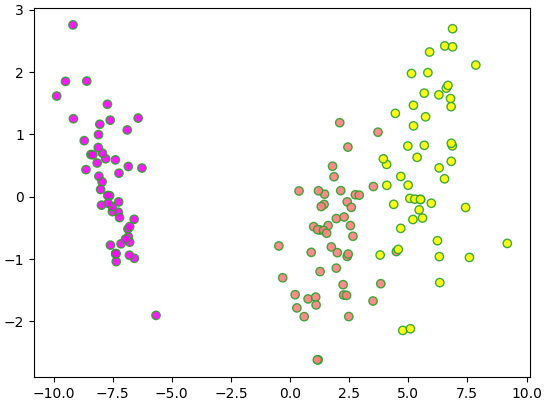
ใช้การวิเคราะห์การจำแนกประเภทเชิงเส้น
ลองทำการวิเคราะห์ข้อมูลในสองมิติโดยการวิเคราะห์การจำแนกประเภทเชิงเส้น (LDA) เพื่อให้ได้ข้อมูลสองมิติที่มีการกระจายตัวดีที่สุด
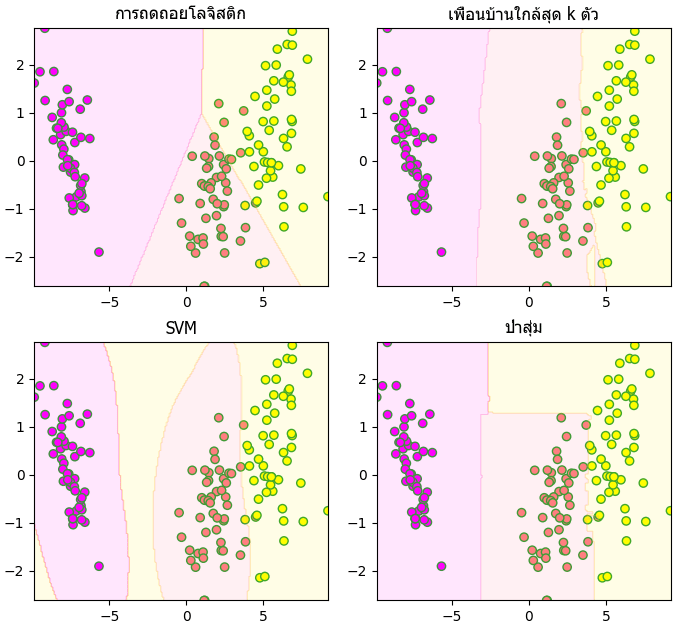
จากนั้นลองทำการลากเส้นแบ่งโดยใช้เทคนิคการเรียนรู้ของเครื่องวิธีต่างๆดู
- การถดถอยโลจิสติก (逻辑回归, logistic regression)
- วิธีการเพื่อนบ้านใกล้สุด k ตัว (K-近邻算法, k-nearest neighbor, KNN)
- เครื่องเวกเตอร์ค้ำยัน (支持向量机, support vector machine, SVM)
- ป่าสุ่ม (随机森林, random forest)
ทดสอบความแม่นยำของเทคนิคต่างๆ
ลองเปรียบเทียบความแม่นยำในการวิเคราะห์ข้อมูลโดยใช้การตรวจสอบแบบไขว้ k-fold (รายละเอียด https://phyblas.hinaboshi.com/20171018)
ได้
จะเห็นว่าแต่ละวิธีสามารถทำการทำนายข้อมูลได้แม่น 90% ขึ้นไป
ใช้ SOM
สุดท้ายลองทำแผนที่โยงก่อร่างตัวเอง (自组织映射, self-organizing maps) หรือ SOM (รายละเอียด https://phyblas.hinaboshi.com/20180805)
ในที่นี้จะใช้คลาส SOM ที่แนะนำไปในบทความนั้น ส่วนนิยามคลาสเอาจากในนี้ได้ https://github.com/phyblas/rianrupython/blob/master/kanrianrukhongkhrueang/som.py
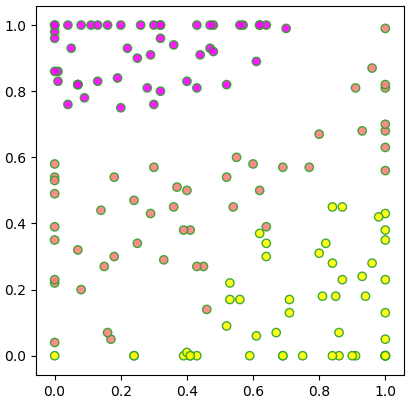
เมื่อใช้ SOM แล้วจะเห็นว่าดอกไม้แต่ละชนิดถูกกระจายลงบนโครงข่ายโดยแต่ละชนิดแยกเขตกันอยู่
จากนั้นลองเอามาทำการแบ่งด้วยเทคนิคต่างๆก็จะได้ออกมาแบบนี้
ชุดข้อมูลนี้เป็นข้อมูลของดอกไม้สกุล Iris ทั้งหมด ๑๕๐ ดอกซึ่งถูกเก็บรวบรวมจากคาบสมุทรกาสเป (Gaspé) ประเทศแคนาดา โดยเอดการ์ แอนเดอร์สัน (Edgar Anderson) นักพฤกษศาสตร์ (บางครั้งจึงเรียกว่าข้อมูลดอกไม้ของแอนเดอร์สัน)
ชุดข้อมูลนี้เริ่มถูกนำมาใช้ในปี 1936 โดยรอนัลด์ ฟิชเชอร์ (Ronald Fisher) นักสถิติ โดยใช้เป็นตัวอย่างในการอธิบายการวิเคราะห์การจำแนกประเภทเชิงเส้น (线性判别分析, linear discriminant analysis)
เรื่องการวิเคราะห์การจำแนกประเภทเชิงเส้นได้เคยแนะนำไปใน https://phyblas.hinaboshi.com/20180802
ข้อมูลดอกไม้ประกอบไปด้วย
0. ความยาวกลีบเลี้ยง
1. ความกว้างกลีบเลี้ยง
2. ความยาวกลีบดอก
3. ความกว้างกลีบดอก
ดอกไม้มี ๓ สายพันธุ์ ได้แก่
0. Iris setosa
1. Iris versicolor
2. Iris virginica
ใน sklearn ได้ใส่ชุดข้อมูลนี้ไว้อยู่ในมอดูลย่อย datasets แล้ว จึงนำมาใช้ได้ง่ายในทันที
from sklearn import datasets
ir = datasets.load_iris()
X = ir.data # ค่าตัวเลขแสดงความกว้างความยาวของกลีบเลี้ยงและกลีบดอก
z = ir.target # เลข 0,1,2 ที่บอกว่าเป็นดอกไม้สายพันธุ์ไหน
print(ir.target_names) # ชื่อสายพันธ์ทั้ง ๓ ของดอกไม้
print(ir.feature_names) # ชื่อค่าแทนลักษณะทั้ง ๔ ที่พิจารณา
print(X.mean(0))ได้
['setosa' 'versicolor' 'virginica']
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
[5.84333333 3.054 3.75866667 1.19866667]เนื่องจากข้อมูลเป็นสี่มิติ การแสดงภาพให้เห็นค่อนข้างยาก อาจลองดูการกระจายในสองมิติโดยจับคู่ดูทีละ ๒ ตัวแปร แบบนี้
import numpy as np
import matplotlib.pyplot as plt
plt.figure(figsize=[6,7])
for i in range(1,4):
for j in range(i):
plt.subplot2grid((3,3),(j,i-1),title='%s<>%s'%(i,j))
plt.scatter(X[:,i],X[:,j],20,c=z,alpha=0.9,edgecolor='C2',cmap='spring')
plt.tight_layout()
plt.show()
ใช้การวิเคราะห์การจำแนกประเภทเชิงเส้น
ลองทำการวิเคราะห์ข้อมูลในสองมิติโดยการวิเคราะห์การจำแนกประเภทเชิงเส้น (LDA) เพื่อให้ได้ข้อมูลสองมิติที่มีการกระจายตัวดีที่สุด
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
lda = LDA(n_components=2)
Xi = lda.fit_transform(X,z)
plt.figure()
plt.scatter(Xi[:,0],Xi[:,1],c=z,alpha=0.9,edgecolor='C2',cmap='spring')
plt.show()
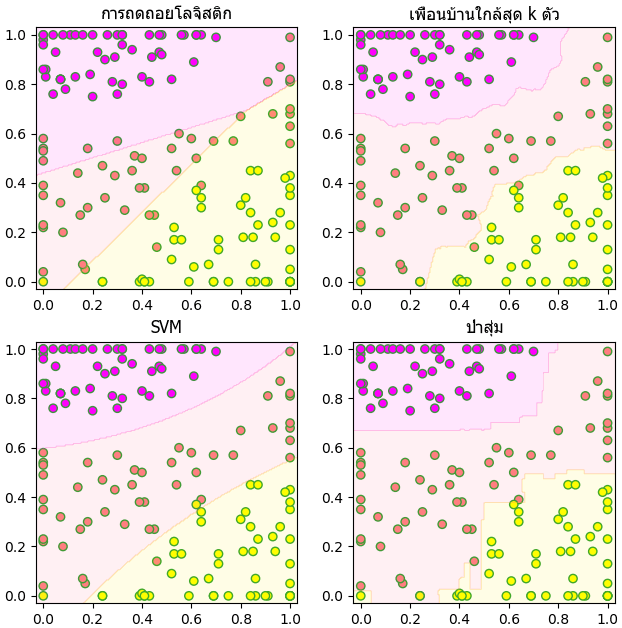
จากนั้นลองทำการลากเส้นแบ่งโดยใช้เทคนิคการเรียนรู้ของเครื่องวิธีต่างๆดู
- การถดถอยโลจิสติก (逻辑回归, logistic regression)
- วิธีการเพื่อนบ้านใกล้สุด k ตัว (K-近邻算法, k-nearest neighbor, KNN)
- เครื่องเวกเตอร์ค้ำยัน (支持向量机, support vector machine, SVM)
- ป่าสุ่ม (随机森林, random forest)
from sklearn.linear_model import LogisticRegression as Lori
from sklearn.neighbors import KNeighborsClassifier as Knn
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier as Rafo
x,y = Xi.T
model = [Lori(),Knn(),SVC(),Rafo()]
withi = [u'การถดถอยโลจิสติก',u'เพื่อนบ้านใกล้สุด k ตัว',u'SVM',u'ป่าสุ่ม']
mx,my = np.meshgrid(np.linspace(x.min(),x.max(),200),np.linspace(y.min(),y.max(),200))
mX = np.array([mx.ravel(),my.ravel()]).T
plt.figure(figsize=[7,7])
for i,m in enumerate(model):
m.fit(Xi,z)
mz = m.predict(mX).reshape(200,200)
plt.subplot(221+i,xlim=[x.min(),x.max()],ylim=[y.min(),y.max()])
plt.scatter(x,y,c=z,edgecolor='C2',cmap='spring')
plt.contourf(mx,my,mz,alpha=0.1,cmap='spring')
plt.title(withi[i],family='Tahoma')
plt.tight_layout()
plt.show()
ทดสอบความแม่นยำของเทคนิคต่างๆ
ลองเปรียบเทียบความแม่นยำในการวิเคราะห์ข้อมูลโดยใช้การตรวจสอบแบบไขว้ k-fold (รายละเอียด https://phyblas.hinaboshi.com/20171018)
from sklearn.model_selection import StratifiedKFold
ir = datasets.load_iris()
X,z = ir.data,ir.target
model = [Lori,Knn,SVC,Rafo]
khanaen = [[],[],[],[]]
for f,t in StratifiedKFold(n_splits=6).split(X,z):
for i,m in enumerate(model):
khanaen[i].append(m().fit(X[f],z[f]).score(X[t],z[t])*100)
khanaen_chalia = np.mean(khanaen,1)
for i in range(4):
print('%s: %.1f%%'%(withi[i],khanaen_chalia[i]))ได้
การถดถอยโลจิสติก: 95.2%
เพื่อนบ้านใกล้สุด k ตัว: 96.6%
SVM: 98.0%
ป่าสุ่ม: 95.9%จะเห็นว่าแต่ละวิธีสามารถทำการทำนายข้อมูลได้แม่น 90% ขึ้นไป
ใช้ SOM
สุดท้ายลองทำแผนที่โยงก่อร่างตัวเอง (自组织映射, self-organizing maps) หรือ SOM (รายละเอียด https://phyblas.hinaboshi.com/20180805)
ในที่นี้จะใช้คลาส SOM ที่แนะนำไปในบทความนั้น ส่วนนิยามคลาสเอาจากในนี้ได้ https://github.com/phyblas/rianrupython/blob/master/kanrianrukhongkhrueang/som.py
from sklearn import datasets
ir = datasets.load_iris()
X,z = ir.data,ir.target
Xsom = SOM([100,100],eta=0.1).rianru_plaeng(X,100) # ใช้ SOM
plt.axes(aspect=1)
plt.scatter(Xsom[:,0],Xsom[:,1],c=z,alpha=0.9,edgecolor='C2',cmap='spring')
plt.show()
เมื่อใช้ SOM แล้วจะเห็นว่าดอกไม้แต่ละชนิดถูกกระจายลงบนโครงข่ายโดยแต่ละชนิดแยกเขตกันอยู่
จากนั้นลองเอามาทำการแบ่งด้วยเทคนิคต่างๆก็จะได้ออกมาแบบนี้

-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy