ต่อจาก บทที่ ๑๘

ในบทนี้จะพูดถึงเรื่องของการแจกแจงความน่าจะเป็นของค่าที่มีพารามิเตอร์การแจกแจงที่มีความไม่แน่นอน ซึ่งการแจกแจงจะมีลักษณะที่เปลี่ยนไป และยังอาจเป็นที่มาของการแจกแจงแบบใหม่




ค่าที่พารามิเตอร์การแจกแจงมีความไม่แน่นอน

ถ้าค่าตัวแปรสุ่ม x ที่พิจารณาอยู่มีการแจกแจกแจงความน่าจะเป็น P(x) ซึ่งขึ้นกับพารามิเตอร์ p แต่ว่าค่า p นั้นเองก็มีความไม่แน่นอนอยู่ โดยมีการแจกแจงความน่าจะเป็นของค่า p เป็น P(p)

ในกรณีแบบนี้การจะหาความน่าจะเป็น P(x) ได้นั้นจะต้องหาความน่าจะเป็นของทุกกรณีที่ p จะเป็นได้ แล้วเอามารวมกันโดยถ่วงน้ำหนักความน่าจะเป็นของกรณีนั้นๆ

หาก p เป็นค่าแบบไม่ต่อเนื่องก็คือหาผลรวม


แต่พารามิเตอร์ p ที่พิจารณานั้นส่วนใหญ่เป็นค่าแบบต่อเนื่องซึ่งกรณีนี้จะคำนวณได้โดยหาปริพันธ์ของฟังก์ชันแจกแจงความหนาแน่น


ถ้าสามารถหาปริพันธ์ออกมาได้ก็จะสามารถหาการแจกแจงความน่าจะเป็นของ x ตามที่ต้องการออกมาได้

อย่างไรก็ตาม นอกจากนั้นแล้วหากรู้อยู่แล้วว่าการแจกแจงที่ได้นั้นควรจะมีลักษณะอย่างไรก็มีอีกวิธีซึ่งถือเป็นวิธีลัดที่ง่ายกว่านั้นอยู่ ซึ่งในบทนี้จะใช้วิธีนั้นเป็นหลัก

ในบทที่ ๑๕ ได้พูดถึงการหาพารามิเตอร์ของการแจกแจงในกรณีที่พารามิเตอร์ของการแจกแจงมีความไม่แน่นอนมีการแจกแจงความน่าจะเป็นก่อนหน้ากำหนดไว้อยู่ โดยใช้การแจกแจงเป็นความน่าจะเป็นก่อนหน้าสังยุค (共轭先验, conjugate prior) ของการแจกแจงนั้น

หากพารามิเตอร์มีการแจกแจงเป็นความน่าจะเป็นก่อนหน้าสังยุคที่เข้าคู่กับการแจกแจงของตัวแปรนั้น เราจะสามารถหาได้ว่าความน่าจะเป็นรวมของค่าที่ได้จะเป็นการแจกแจงแจงดังนี้

การแจกแจงค่าเมื่อกำหนดพารามิเตอร์ $P(x|p)$	พารามิเตอร์ $p$	การแจกแจงของพารามิเตอร์ $\mathcal{P}(p), \mathcal{P}(p|x)$	การแจกแจงโดยรวมของค่าตัวแปรที่ได้ $P(x)$
การแจกแจงทวินาม	p	การแจกแจงเบตา	การแจกแจงเบตา-ทวินาม
การแจกแจงทวินามเชิงลบ	p	การแจกแจงเบตา	การแจกแจงเบตา-ทวินามเชิงลบ
การแจกแจงอเนกนาม	p	การแจกแจงดีริคเล	การแจกแจงดีริคเล-อเนกนาม
การแจกแจงปัวซง	λ	การแจกแจงแกมมา	การแจกแจงทวินามเชิงลบ
การแจกแจงแบบเลขชี้กำลัง	λ	การแจกแจงแกมมา	การแจกแจงโลแม็กซ์
การแจกแจงแบบปกติ	μ	การแจกแจงแบบปกติ	การแจกแจงแบบปกติ
	α (=1/σ2)	การแจกแจงแกมมา	การแจกแจงสติวเดนต์ที
การแจกแจงแบบปกติหลายตัวแปร	μ	การแจกแจงแบบปกติหลายตัวแปร	การแจกแจงแบบปกติหลายตัวแปร
	Λ (=Σ-1)	การแจกแจงวิชาร์ต	การแจกแจงสติวเดนต์ทีหลายตัวแปร

ที่จริงนี่คือตารางเดิมจากบทที่ ๑๕ แต่แค่เพิ่มส่วนของการแจกแจงโดยรวมที่จะได้ในแต่ละกรณีลงไป

จะเห็นว่าบางส่วนจะได้เป็นการแจกแจงชนิดเดิม แต่ก็มีที่ได้เป็นการแจกแจงชนิดใหม่ (บางส่วนก็แค่เอาชื่อมาต่อกัน)

หากเรารู้อยู่แล้วว่าการแจกแจงที่ได้นั้นควรจะเป็นการแจกแจงแบบไหน สามารถใช้วิธีการพิจารณาสมการทฤษฎีบทของเบส์ โดยมองแค่ส่วนที่เกี่ยวข้องกับ x แล้วให้ส่วนที่ไม่เกี่ยวข้องไปรวมอยู่กับค่าคงที่

สมการทฤษฎีบทของเบส์เมื่อพิจารณาตัวแปร x และพารามิเตอร์ p คือ


ดังนั้นการแจกแจงความน่าจะเป็นโดยรวมของ x ก็สามารถคำนวณได้จากสมการนี้


ในที่นี้จะพิจารณาเอาส่วนที่ไม่เกี่ยวกับ x มารวมไว้เป็นค่าคงที่ ซึ่งการแจกแจงความน่าจะเป็นก่อนหน้าไม่เกี่ยวข้องกับ x จึงสามารถให้เป็นค่าคงที่ $\mathcal{P}(p) = \mathcal{C}$ จึงได้ว่า


ดังนั้นการแจกแจงของ x ที่หาอยู่ก็ขึ้นอยู่กับรูปแบบการแจกแจงเดิมของ x นั้นเอง และการแจกแจงของพารามิเตอร์ p นั้น

ในบทนี้ส่วนที่เหลือจะยกตัวอย่างกรณีการแจกแจงบางส่วนที่สำคัญ ได้แก่กรณีของการแจกแจงปัวซง และกรณีของการแจกแจงแบบปกติเมื่อพารามิเตอร์ที่พิจารณาเป็น μ

ส่วนการแจกแจงแบบปกติในกรณีที่พิจารณา α นั้นจะได้การแจกแจงสติวเดนต์ที ซึ่งยังไม่เคยกล่าวถึง และค่อนข้างมีความสำคัญและมีรายละเอียดมาก จึงขอยกไปกล่าวถึงเป็นบทหน้าโดยเฉพาะ




การแจกแจงแบบปกติที่ μ มีความไม่แน่นอน

ขอเริ่มยกตัวอย่างจากกรณีการแจกแจงแบบปกติที่พิจารณาค่าพารามิเตอร์ μ ซึ่งดูจะเข้าใจง่ายที่สุด เพราะทั้งการแจกแจงของ μ เองก็เป็นการแจกแจงแบบปกติ และการแจกแจงของ x ที่ได้สุดท้ายก็จะเป็นการแจกแจงแบบปกติอีกเช่นกัน

การแจกแจงความน่าจะเป็นโดยรวมของ x ในที่นี้จะคำนวณได้จาก


การแจกแจงความน่าจะเป็นของ x (หรือก็คือฟังก์ชันควรจะเป็น) ก็คือการแจกแจงแบบปกติ ที่มีใจกลางที่ μ และความแปรปรวน σ²


ดึงค่าที่ไม่เกี่ยวกับ x มาไว้ใน $\mathcal{C}$


สำหรับการแจกแจงความน่าจะเป็นของ μ ในที่นี้ก็จะตรงกับการแจกแจงความน่าจะเป็นภายหลังนั้นซึ่งได้แสดงวิธีหาไปในบทที่ ๑๕ ในที่นี้จึงขอยกผลจากบทนั้นมาใช้เลย


จากนั้นก็จัดรูป ดึงส่วนที่ไม่เกี่ยวข้องกับ x มาไว้ในค่าคงที่ $\mathcal{C}$


แทนผลจากสมการ 19.8 และ 19.10 ลงในสมการ 19.6 แล้วจัดรูปต่อ ได้


สุดท้ายก็จะเห็นว่าการแจกแจงของ x ในที่นี้ก็สามารถเขียนในรูปของการแจกแจงแบบปกติเช่นกัน โดยจุดกึ่งกลางการแจกแจงของ x ก็คือจุดกึ่งกลางการแจกแจงของ μ นั่นเอง ซึ่งตรงนี้ก็เป็นสิ่งที่คาดการณ์ได้ไม่ยาก เพราะจุดที่มีความน่าจะเป็นของ μ มากที่สุดก็ย่อมมีความน่าจะเป็นของ x สูงสุดด้วย

ส่วนค่าความแปรปรวน σ² จะได้เป็นผลรวมระหว่างความแปรปรวนของ x ซึ่งทราบค่าอยู่แล้ว กับความแปรปรวนของ μ จากการแจกแจงซึ่งคาดการณ์ไว้ตอนแรก

ต่อไปเป็นโค้ดตัวอย่างการจำลองให้เห็นจริง โดยจะเริ่มจากสุ่มค่า μ ก่อน แล้วใช้ค่า μ ที่สุ่มได้นั้นมาเป็นพารามิเตอร์ในการสุ่มของ x อีกที ซึ่งค่า x ที่ได้ก็ควรจะเป็นการแจกแจงแบบปกติที่มีความแปรปรวนเป็นผลรวมของความแปรปรวนของการแจกแจงทั้งสองนั้น ในที่นี้จะแสดงฮิสโทแกรมของผลการแจกแจง และวาดกราฟที่ได้จากการคำนวณลงไปด้วย

import numpy as np
import random,math

# ฟังก์ชันการแจกแจงแบบปกติ
def pakati(x,μ,σ):
    return (2*np.pi)**(-0.5)/σ*np.exp(-(x-μ)**2/(2*σ**2))

μ_μ = 8 # จุดกึ่งกลางของ μ
σ_μ = 3 # ส่วนเบี่ยงเบนมาตรฐานของ μ
σ = 4 # ส่วนเบี่ยงเบนมาตรฐานของ x

x = []
for i in range(2345):
    μ = random.gauss(μ_μ,σ_μ)
    x += [random.gauss(μ,σ)]

# วาดฮิสโทแกรมแสดงความหนาแน่น
plt.hist(x,50,fc='#b5c92f',ec='w',density=True)
# วาดเส้นแสดงค่าจริงที่ได้จากการคำนวณ
x_ = np.linspace(min(x),max(x),201)
Px_ = pakati(x_,μ_μ,(σ**2+σ_μ**2)**0.5)
plt.plot(x_,Px_,'#953a25')
plt.show()

ผลที่ได้



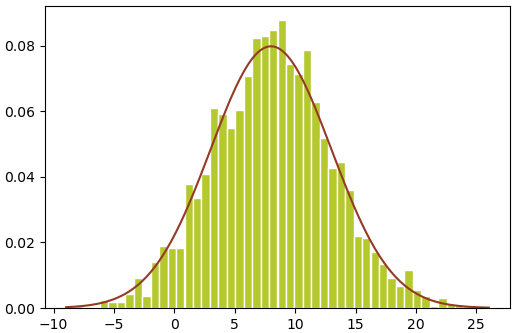
ในที่นี้ให้จุดกึ่งกลางการแจกแจงอยู่ที่ μ_μ=8 ให้ความแปรปรวนของ x เป็น σ=4² ความแปรปรวนของ μ เป็น σ_μ=3² ดังนั้นการแจกแจงสุดท้ายของ x ควรมีความแปรปรวนเป็น 3²+4²=5²

เส้นกราฟคือค่าที่ได้จากการคำนวณ และฮิสโทแกรมแสดงการแจกแจงที่ได้จริงๆ ผลที่ได้จะเห็นว่ากราฟกับฮิสโทแกรมสอดคล้องกันดี




การแจกแจงปัวซงที่ λ มีความไม่แน่นอน

ต่อมาดูการแจกแจงปัวซง ซึ่งค่า λ มีความน่าจะเป็นก่อนหน้าสังยุคเป็นการแจกแจงแกมมา ซึ่งเมื่อ λ มีการแจกแจงตามนั้นแล้ว ผลการแจกแจงที่ได้ก็จะออกมาเป็นการแจกแจงทวินามเชิงลบ

ให้ตัวแปรสุ่ม k เป็นผลจากการแจกแจงปัวซงซึ่งมีพารามิเตอร์ λ ซึ่งมีความไม่แน่นอนอยู่ การแจกแจงของ k ที่จะได้ในท้ายที่สุดอาจหาได้จากทฤษฎีบทของเบส์ดังนี้


ซึ่งการแจกแจงก่อนหน้า P(λ) ไม่ได้เกี่ยวกับค่าตัวแปร k ที่พิจารณา จึงให้เป็นค่าคงที่


พิจารณาการแจกแจงของค่า k ซึ่งเป็นการแจกแจงปัวซงเป็น


สำหรับการแจกแจงของพารามิเตอร์ λ ก็คือการแจกแจงความน่าจะเป็นภายหลัง ดังที่ได้แสดงไว้ในบทที่ ๑๖ จากนั้นก็จัดรูป ดึงส่วนที่ไม่เกี่ยวข้องกับ x มาไว้ในค่าคงที่ $\mathcal{C}$


จากนั้นแทนสมการ 19.14 และ 19.15 ลงในสมการ 19.13


ซึ่งจะเห็นว่าได้ลักษณะที่สามารถเขียนออกมาเป็นการแจกแจงทวินามเชิงลบได้

การแจกแจงทวินามเชิงลบได้เขียนถึงไปในบทที่ ๖ ขอยกสมการจากตรงนั้นมา


เมื่อเทียบสมการ 19.16 กับ 19.17 แล้วจะได้ว่าในที่นี้


แล้วค่าคงที่ด้านหน้าก็คือ


ดังนั้นสุดท้ายแล้วได้การแจกแจงของค่า k คือ




บทถัดไป >> บทที่ ๒๐

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文