โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๒: ออปทิไมเซอร์
เขียนเมื่อ 2018/08/26 23:31
แก้ไขล่าสุด 2022/07/10 21:09
>> ต่อจาก บทที่ ๑๑
ในบทที่ผ่านๆมาทั้งหมดใช้วิธีการเคลื่อนลงตามความชัน (梯度下降法, gradient descent) ในการปรับค่าพารามิเตอร์
แต่ว่าแค่เคลื่อนลงตามความชันเฉยๆแบบธรรมดานั้นยังไม่ดีพอ จึงได้มีคนคิดวิธีต่างๆในการทำให้มีประสิทธิภาพมากขึ้น แม้ว่าจะมีการคำนวณที่ซับซ้อนขึ้นสักหน่อย
วิธีการในการปรับปรุงการเคลื่อนลงตามความชันแบบดั้งเดิมนั้นมีอยู่หลายแบบ เช่น
- โมเมนตัม
- AdaGrad
- AdaDelta
- RMSprop
- Adam
เกี่ยวกับเรื่องนี้ได้เขียนแนะนำไปในหน้านี้ https://phyblas.hinaboshi.com/20171002
ดังนั้นเพื่อไม่ให้ซ้ำ ในนี้จะไม่อธิบายโดยละเอียด ก่อนอื่นให้ไปอ่านในนั้น
สำหรับตอนนี้จะพูดถึงแค่วิธีการนำวิธีการเหล่านั้นมาใช้ในโครงข่ายประสาทเทียม
ทำได้โดยสร้างคลาสของวิธีการแต่ละชนิดขึ้นมา
ก่อนอื่นให้ไปเอาคลาสของตัวแปรและชั้นต่างๆที่ใช้ในบทที่ ๑๑ เพื่อความสะดวกจึงได้รวมไว้แล้วที่ unagi.py
อาจโหลดทั้งไฟล์มาแล้วเรียกใช้ในฐานะมอดูลได้เลย
จากนั้นเราจะสร้างคลาสของตัวปรับพารามิเตอร์แต่ละชนิดขึ้น
คลาสตัวปรับพารามิเตอร์พวกนี้มักถูกเรียว่า ออปทิไมเซอร์ (optimizer) แปลว่าตัวสำหรับปรับอะไรให้ออกมาดีที่สุด
ออปทิไมเซอร์จะเก็บบันทึกไว้ว่าพารามิเตอร์ตัวไหนบ้างที่ต้องการจะปรับค่า จากนั้นเวลาที่ถูกเรียกใช้ก็จะทำการปรับค่าของพารามิเตอร์เหล่านั้นตามค่าอนุพันธ์ที่ถูกคำนวณไว้หลังการแพร่ย้อนกลับ
ถ้าใช้ Sgd ก็จะเหมือนกับในบทที่ผ่านๆมา คือแค่เอาอัตราเรียนรู้ eta มาคูณกับอนุพันธ์
แต่ถ้าใช้ตัวอื่นๆจะมีการคำนวณที่ซับซ้อนขึ้นไปซึ่งช่วยให้ผลออกมาดีขึ้น รายละเอียดลองดูที่ส่วนนิยามคลาสแต่ละตัวได้
ในจำนวนนี้ Adam มีคนแนะนำให้ใช้มากที่สุด หากไม่ได้มีเหตุผลที่จะเลือกอันไหนเป็นพิเศษส่วนใหญ่จะเลือก Adam ไว้ก่อน
ตัวอย่างการสร้างคลาสที่นำมาใช้
ในที่นี้ในคลาสได้สร้างเมธอด .param() เอาไว้ใช้ค้นเอาพารามิเตอร์จากทุกชั้นที่มี จากนั้นก็ส่งพารามิเตอร์นี้ให้ออปติไมเซอร์
จากนั้นตอนท้ายสุดของแต่ละรอบหลังจากที่คำนวณไปข้างหน้าและแพร่ย้อนกลับแล้วก็เรียกใช้ออปติไมเซอร์ เท่านี้ค่าพารามิเตอร์ก็จะถูกปรับ
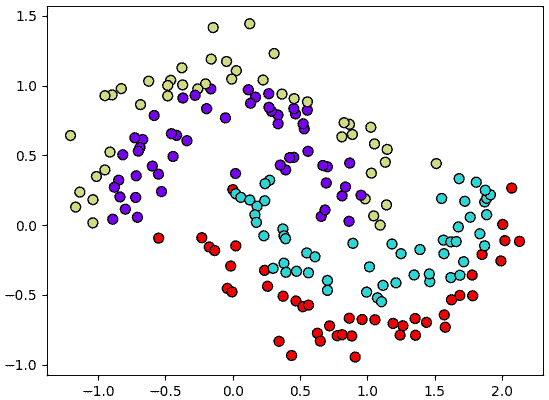
ต่อไปก็ลองเอามาใช้ ขอยกข้อมูล ๔ กลุ่มที่กระจายตัวแบบนี้
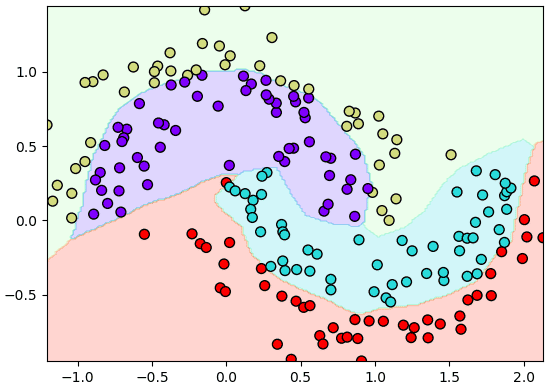
ลองสร้างเป็นโครงข่ายสัก ๓ ชั้น ใช้ ReLU เป็นฟังก์ชันกระตุ้น ส่วนออปทิไมเซอร์ก็เลือก Adam
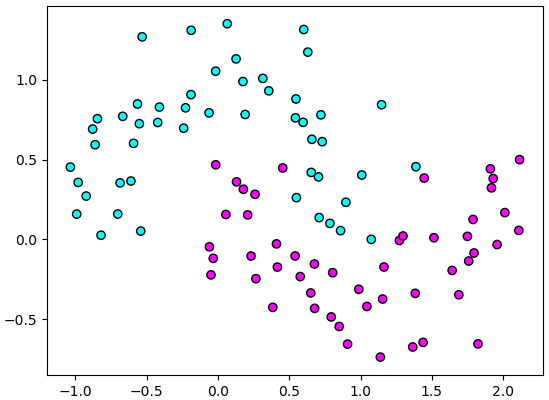
ต่อมาลองยกอีกตัวอย่างเพื่อเปรียบเทียบการเรียนรู้ของออปติไมเซอร์แบบต่างๆ คราวนี้ลองไม่สร้างเป็นคลาส พิจารณาปัญหาจำแนกสองกลุ่มรูปเสี้ยวพระจันทร์อย่างง่ายๆดู
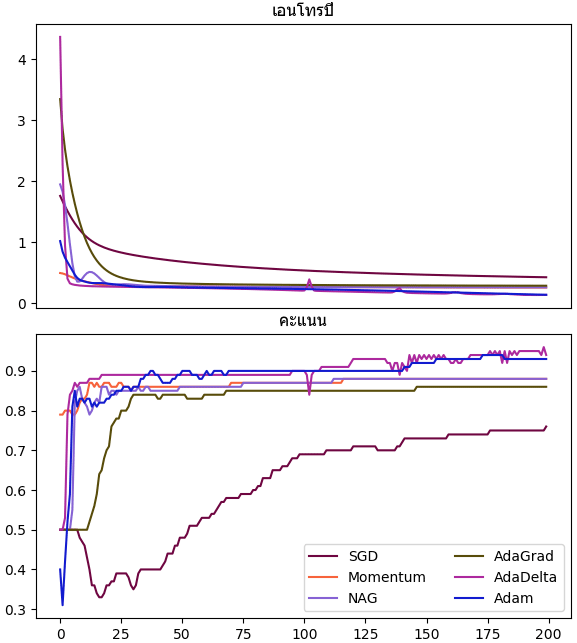
เทียบแล้วแต่ละวิธีมีสภาพความคืบหน้าต่างกันไป แต่โดยรวมแล้ว SGD ธรรมดาจะดูด้อยที่สุด
อนึ่ง ออปทิไมเซอร์ที่สร้างในบทนี้เขียนให้ทำการลบค่าอนุพันธ์ให้เป็น 0 ทันทีที่ทำการปรับค่าแล้ว
แต่เวลาใช้งานจริงอย่างใน pytorch จะไม่ทำแบบนั้น แต่จะมีเมธอดชื่อ .zero_grad() ซึ่งเราต้องเขียนสั่งทุกครั้งหลังคำนวณเสร็จแต่ละที
ที่ทำแบบนั้นเพราะในบางกรณีเราอาจยังต้องเก็บค่าอนุพันธ์ไว้ใช้ต่อ ถ้าล้างทิ้งเลยจะใช้ต่อไม่ได้แล้ว
แต่ในที่นี้เพื่อความง่ายจึงให้ล้างทิ้งทันทีเพื่อลดความซับซ้อนของโค้ดลง
>> อ่านต่อ บทที่ ๑๓
ในบทที่ผ่านๆมาทั้งหมดใช้วิธีการเคลื่อนลงตามความชัน (梯度下降法, gradient descent) ในการปรับค่าพารามิเตอร์
แต่ว่าแค่เคลื่อนลงตามความชันเฉยๆแบบธรรมดานั้นยังไม่ดีพอ จึงได้มีคนคิดวิธีต่างๆในการทำให้มีประสิทธิภาพมากขึ้น แม้ว่าจะมีการคำนวณที่ซับซ้อนขึ้นสักหน่อย
วิธีการในการปรับปรุงการเคลื่อนลงตามความชันแบบดั้งเดิมนั้นมีอยู่หลายแบบ เช่น
- โมเมนตัม
- AdaGrad
- AdaDelta
- RMSprop
- Adam
เกี่ยวกับเรื่องนี้ได้เขียนแนะนำไปในหน้านี้ https://phyblas.hinaboshi.com/20171002
ดังนั้นเพื่อไม่ให้ซ้ำ ในนี้จะไม่อธิบายโดยละเอียด ก่อนอื่นให้ไปอ่านในนั้น
สำหรับตอนนี้จะพูดถึงแค่วิธีการนำวิธีการเหล่านั้นมาใช้ในโครงข่ายประสาทเทียม
ทำได้โดยสร้างคลาสของวิธีการแต่ละชนิดขึ้นมา
ก่อนอื่นให้ไปเอาคลาสของตัวแปรและชั้นต่างๆที่ใช้ในบทที่ ๑๑ เพื่อความสะดวกจึงได้รวมไว้แล้วที่ unagi.py
อาจโหลดทั้งไฟล์มาแล้วเรียกใช้ในฐานะมอดูลได้เลย
from unagi import Affin,Sigmoid,Relu,Softmax_entropy,Sigmoid_entropy,ha_1hจากนั้นเราจะสร้างคลาสของตัวปรับพารามิเตอร์แต่ละชนิดขึ้น
import numpy as np
import matplotlib.pyplot as plt
class Sgd:
def __init__(self,param,eta=0.01):
self.param = param
self.eta = eta
def __call__(self):
for p in self.param:
p.kha -= self.eta*p.g
p.g = 0
class Mmtsgd:
def __init__(self,param,eta=0.01,mmt=0.9):
self.param = param
self.eta = eta
self.mmt = mmt
self.d = [0]*len(param)
def __call__(self):
for i,p in enumerate(self.param):
self.d[i] = self.mmt*self.d[i]-self.eta*p.g
p.kha += self.d[i]
p.g = 0
class Nag:
def __init__(self,param,eta=0.01,mmt=0.9):
self.param = param
self.eta = eta
self.mmt = mmt
self.d = [0]*len(param)
self.g0 = np.nan
def __call__(self):
if(self.g0 is np.nan):
self.g0 = [p.g for p in self.param]
for i,p in enumerate(self.param):
self.d[i] = self.mmt*self.d[i]-self.eta*(p.g+self.mmt*(p.g-self.g0[i]))
self.g0[i] = p.g
p.kha += self.d[i]
p.g = 0
class Adagrad:
def __init__(self,param,eta=0.01):
self.param = param
self.eta = eta
self.G = [1e-7]*len(param)
def __call__(self):
for i,p in enumerate(self.param):
self.G[i] += p.g**2
p.kha += -self.eta*p.g/np.sqrt(self.G[i])
p.g = 0
class Adadelta:
def __init__(self,param,eta=0.01,rho=0.95):
self.param = param
self.eta = eta
self.rho = rho
self.G = [1e-7]*len(param)
def __call__(self):
for i,p in enumerate(self.param):
self.G[i] = self.rho*self.G[i]+(1-self.rho)*p.g**2
p.kha += -self.eta*p.g/np.sqrt(self.G[i])
p.g = 0
class Adam:
def __init__(self,param,eta=0.001,beta1=0.9,beta2=0.999):
self.param = param
self.eta = eta
self.beta1 = beta1
self.beta2 = beta2
n = len(param)
self.m = [0]*n
self.v = [1e-7]*n
self.t = 1
def __call__(self):
for i,p in enumerate(self.param):
self.m[i] = self.beta1*self.m[i]+(1-self.beta1)*p.g
self.v[i] = self.beta2*self.v[i]+(1-self.beta2)*p.g**2
p.kha += -self.eta*np.sqrt(1-self.beta2**self.t)/(1-self.beta1**self.t)*self.m[i]/np.sqrt(self.v[i])
self.t += 1
p.g = 0
คลาสตัวปรับพารามิเตอร์พวกนี้มักถูกเรียว่า ออปทิไมเซอร์ (optimizer) แปลว่าตัวสำหรับปรับอะไรให้ออกมาดีที่สุด
ออปทิไมเซอร์จะเก็บบันทึกไว้ว่าพารามิเตอร์ตัวไหนบ้างที่ต้องการจะปรับค่า จากนั้นเวลาที่ถูกเรียกใช้ก็จะทำการปรับค่าของพารามิเตอร์เหล่านั้นตามค่าอนุพันธ์ที่ถูกคำนวณไว้หลังการแพร่ย้อนกลับ
ถ้าใช้ Sgd ก็จะเหมือนกับในบทที่ผ่านๆมา คือแค่เอาอัตราเรียนรู้ eta มาคูณกับอนุพันธ์
แต่ถ้าใช้ตัวอื่นๆจะมีการคำนวณที่ซับซ้อนขึ้นไปซึ่งช่วยให้ผลออกมาดีขึ้น รายละเอียดลองดูที่ส่วนนิยามคลาสแต่ละตัวได้
ในจำนวนนี้ Adam มีคนแนะนำให้ใช้มากที่สุด หากไม่ได้มีเหตุผลที่จะเลือกอันไหนเป็นพิเศษส่วนใหญ่จะเลือก Adam ไว้ก่อน
ตัวอย่างการสร้างคลาสที่นำมาใช้
class Prasat:
def __init__(self,m,sigma=1,eta=0.1,kratun='relu',opt='adam'):
self.m = m
self.chan = []
for i in range(len(m)-1):
self.chan.append(Affin(m[i],m[i+1],sigma))
if(i<len(m)-2):
if(kratun=='relu'):
self.chan.append(Relu())
else:
self.chan.append(Sigmoid())
self.chan.append(Softmax_entropy())
opt = {'adam':Adam,'adagrad':Adagrad,
'adadelta':Adadelta,'mmtsgd':Mmtsgd,
'sgd':Sgd,'nag':Nag}[opt]
self.opt = opt(self.param(),eta=eta)
def rianru(self,X,z,n_thamsam):
Z = ha_1h(z,self.m[-1])
for i in range(n_thamsam):
entropy = self.ha_entropy(X,Z)
entropy.phraeyon()
self.opt()
def ha_entropy(self,X,Z):
for c in self.chan[:-1]:
X = c(X)
return self.chan[-1](X,Z)
def param(self):
p = []
for c in self.chan:
if(hasattr(c,'param')):
p.extend(c.param)
return p
def thamnai(self,X):
for c in self.chan[:-1]:
X = c(X)
return X.kha.argmax(1)ในที่นี้ในคลาสได้สร้างเมธอด .param() เอาไว้ใช้ค้นเอาพารามิเตอร์จากทุกชั้นที่มี จากนั้นก็ส่งพารามิเตอร์นี้ให้ออปติไมเซอร์
จากนั้นตอนท้ายสุดของแต่ละรอบหลังจากที่คำนวณไปข้างหน้าและแพร่ย้อนกลับแล้วก็เรียกใช้ออปติไมเซอร์ เท่านี้ค่าพารามิเตอร์ก็จะถูกปรับ
ต่อไปก็ลองเอามาใช้ ขอยกข้อมูล ๔ กลุ่มที่กระจายตัวแบบนี้
np.random.seed(12)
t = np.linspace(0,360,200)
r = np.random.normal(1,0.2,200)
x = r*np.cos(np.radians(t))
y = r*np.sin(np.radians(t))
z = (t>180)*1
x += z
y += z/3.
z += (r>1)*2
X = np.array([x,y]).T
plt.scatter(X[:,0],X[:,1],50,c=z,edgecolor='k',cmap='rainbow')
plt.show()
ลองสร้างเป็นโครงข่ายสัก ๓ ชั้น ใช้ ReLU เป็นฟังก์ชันกระตุ้น ส่วนออปทิไมเซอร์ก็เลือก Adam
prasat = Prasat(m=[2,70,70,4],eta=0.1)
prasat.rianru(X,z,n_thamsam=1000)
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),200),np.linspace(X[:,1].min(),X[:,1].max(),200))
mX = np.array([mx.ravel(),my.ravel()]).T
mz = prasat.thamnai(mX).reshape(200,-1)
plt.axes(aspect=1,xlim=(X[:,0].min(),X[:,0].max()),ylim=(X[:,1].min(),X[:,1].max()))
plt.contourf(mx,my,mz,cmap='rainbow',alpha=0.2)
plt.scatter(X[:,0],X[:,1],50,c=z,edgecolor='k',cmap='rainbow')
plt.show()
ต่อมาลองยกอีกตัวอย่างเพื่อเปรียบเทียบการเรียนรู้ของออปติไมเซอร์แบบต่างๆ คราวนี้ลองไม่สร้างเป็นคลาส พิจารณาปัญหาจำแนกสองกลุ่มรูปเสี้ยวพระจันทร์อย่างง่ายๆดู
t = np.linspace(0,360,100)
r = np.random.normal(1,0.2,100)
x = r*np.cos(np.radians(t))
y = r*np.sin(np.radians(t))
z = np.array([0,1]).repeat(50)
x += z
y += z/2.
X = np.array([x,y]).T
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='cool')
plt.figure(figsize=[6,10])
ax1 = plt.subplot(211,xticks=[])
ax1.set_title(u'เอนโทรปี',family='Tahoma')
ax2 = plt.subplot(212)
ax2.set_title(u'คะแนน',family='Tahoma')
for Opt in [Sgd,Mmtsgd,Nag,Adagrad,Adadelta,Adam]:
chan = [Affin(2,60,1),Sigmoid(),Affin(60,1,1),Sigmoid_entropy()]
opt = Opt(chan[0].param+chan[2].param,eta=0.02)
lis_entropy = []
lis_khanaen = []
for i in range(200):
X_ = X
for c in chan[:-1]:
X_ = c(X_)
lis_khanaen.append(((X_.kha.ravel()>0)==z).mean())
entropy = chan[-1](X_,z)
lis_entropy.append(entropy.kha)
entropy.phraeyon()
opt()
si = np.random.random(3)
ax1.plot(lis_entropy,color=si)
ax2.plot(lis_khanaen,color=si)
plt.legend(['SGD','Momentum','NAG','AdaGrad','AdaDelta','Adam'],ncol=2)
plt.tight_layout()
plt.show()

เทียบแล้วแต่ละวิธีมีสภาพความคืบหน้าต่างกันไป แต่โดยรวมแล้ว SGD ธรรมดาจะดูด้อยที่สุด
อนึ่ง ออปทิไมเซอร์ที่สร้างในบทนี้เขียนให้ทำการลบค่าอนุพันธ์ให้เป็น 0 ทันทีที่ทำการปรับค่าแล้ว
แต่เวลาใช้งานจริงอย่างใน pytorch จะไม่ทำแบบนั้น แต่จะมีเมธอดชื่อ .zero_grad() ซึ่งเราต้องเขียนสั่งทุกครั้งหลังคำนวณเสร็จแต่ละที
ที่ทำแบบนั้นเพราะในบางกรณีเราอาจยังต้องเก็บค่าอนุพันธ์ไว้ใช้ต่อ ถ้าล้างทิ้งเลยจะใช้ต่อไม่ได้แล้ว
แต่ในที่นี้เพื่อความง่ายจึงให้ล้างทิ้งทันทีเพื่อลดความซับซ้อนของโค้ดลง
>> อ่านต่อ บทที่ ๑๓
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy