[python] แนวทางต่างๆในการปรับปรุงวิธีการเคลื่อนลงตามความชัน
เขียนเมื่อ 2017/10/02 16:18
แก้ไขล่าสุด 2022/07/21 15:18
วิธีการเคลื่อนลงตามความชัน (梯度下降法, gradient descent, GD) หรือ เคลื่อนลงตามความชันแบบสุ่ม (随机梯度下降法, stochastic gradient descent, SGD) เป็นวิธีการสำคัญที่ใช้ในปรับค่าพารามิเตอร์ (น้ำหนักและไบแอส) ในการเรียนรู้ของเครื่อง
รายละเอียดได้เขียนถึงเอาไว้ตั้งแต่บทความช่วงแรก https://phyblas.hinaboshi.com/20161210
ในการเคลื่อนลงตามความชันแบบธรรมดานั้นโดยพื้นฐานแล้วการเปลี่ยนแปลงค่าของพารามิเตอร์จะขึ้นกับอัตราการเรียนรู้ (学习率, learning rate) ล้วนๆ ซึ่งอัตราการเรียนรู้นี้จะคงที่ตลอดไม่ว่าจะวนซ้ำเพื่อฝึกไปกี่ครั้ง
การที่อัตราการเรียนรู้คงที่นั้นเป็นวิธีการที่เป็นเบื้องต้นเรียบง่าย แต่ต่อมาก็ได้มีคนพยายามจะปรับปรุงหาวิธีทำให้การปรับค่าพารามิเตอร์ขึ้นกับปัจจัยต่างๆมากขึ้น
ในที่นี้จะแนะนำวิธีหลักๆที่คนนิยมใช้กันอยู่ตอนนี้ ได้แก่ โมเมนตัม, NAG, AdaGrad, AdaDelta, RMSprop, Adam
โมเมนตัม (momentum)
โมเมนตัมคือปริมาณที่บอกสภาพการเคลื่อนที่ของวัตถุ ปกติเราจะคุ้นกับโมเมนตัมในทางฟิสิกส์ เวลาของกลิ้งตกจากที่สูงลงที่ต่ำมันไม่ได้เคลื่อนลงในทิศเดียวกับความชันเสียทีเดียว ปกติแล้วสิ่งที่กำลังเคลื่อนที่จะมีความเฉื่อย ต่อให้มีแรงมากระทำในทิศทางอื่นแต่มันก็จะยังคงจะเคลื่อนที่ต่อไปในทางเดิมอยู่
สำหรับโมเมนตัมที่ใช้ในวิธีการเคลื่อนลงตามความชันในที่นี้ก็มีหลักการคล้ายๆกัน คือสร้างผลที่เสมือนกับการเคลื่อนที่ของวัตถุที่มีความเฉื่อยเข้ามา
หากใส่โมเมนตัมเข้าไป เวลาคำนวนตำแหน่งต่อไปจะมีผลจากการเคลื่อนไหวในขั้นก่อนหน้านี้มาเกี่ยวด้วย โดยจะพยายามรักษาทิศการเคลื่อนที่ในแนวเดิม
จากที่เดิมทีค่าใหม่จะขึ้นกับความชันและอัตราการเรียนรู้เท่านั้น คือ
..(1)
ในที่นี้ w คือพารามิเตอร์น้ำหนักที่ต้องการปรับ η คืออัตราการเรียนรู้ ส่วน t คือเลขที่บอกว่าเป็นขั้นที่เท่าไหร่
สัญลักษณ์เว็กเตอร์ในที่นี้แสดงว่าเป็นปริมาณที่มีหลายมิติ เช่นค่าพารามิเตอร์น้ำหนัก w⃗ ก็แบ่งเป็น w1,w2,... ถ้าเป็นในโปรแกรมก็คือเป็นตัวแปรที่เป็นอาเรย์นั่นเอง
ส่วน g⃗ คืออนุพันธ์ย่อย (ก็คือความชัน) ของฟังก์ชันค่าเสียหาย J ที่ตำแหน่ง wt
..(2)
ค่าน้ำหนักในขั้นนี้ตอนต่อไปจะเปลี่ยนแปลงไป Δw นั่นคือ
..(3)
ทีนี้ต่อหากเพิ่มโมเมนตัมเข้าไป สมการ (1) จะกลายเป็นแบบนี้
..(4)
ที่เพิ่มเข้ามาคือพจน์ αΔw⃗t โดย α ในที่นี้คือขนาดของโมเมนตัม ค่าที่มักจะใช้กันคือ 0.9 ถ้าหากพจน์นี้เป็น 0 ก็จะเท่ากับการเคลื่อนลงตามความชันธรรมดาที่ไม่มีโมเมนตัม
จากสมการจะเห็นได้ว่าพจน์ที่เพิ่มเข้ามาจะช่วยให้การเปลี่ยนแปลงจากขั้นที่แล้วยังมีผลอยู่ด้วย นั่นเท่ากับเป็นการพยายามรักษาการเคลื่อนที่ ดังนั้นเส้นทางการเคลื่อนที่จะดูคล้ายกับวัตถุจริงมากขึ้น
เมื่อเพิ่มมาแล้วผลจะเป็นยังไงลองมาสร้างตัวอย่างขึ้นแล้วเพื่อเปรียบเทียบผลที่ได้กันดู
สมมุติว่าฟังก์ชันค่าเสียหายขึ้นกับตัวแปรสองตัวเป็นดังนี้
..(5)
หาอนุพันธ์ได้ดังนี้
..(6)
..(7)
ลองเขียนเป็นฟังก์ชันในไพธอนได้ดังนี้
จากค่าความชันที่ได้คงดูออกได้ไม่ยากว่าจุดต่ำสุดควรอยู่ที่จุด (5,-0.25) นี่คือเป้าหมายที่ต้องการมุ่งไปให้ถึง
ลองตั้งจุดเริ่มต้นสักจุด ในที่นี้ลองเริ่มจาก (-7,2) แล้วก็เริ่มปรับค่าโดยวิธีเคลื่อนลงตามความชันแบบธรรมดาจะเป็นแบบนี้
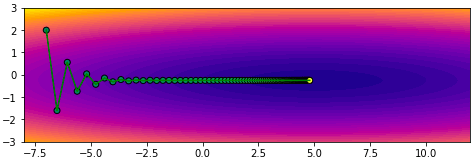
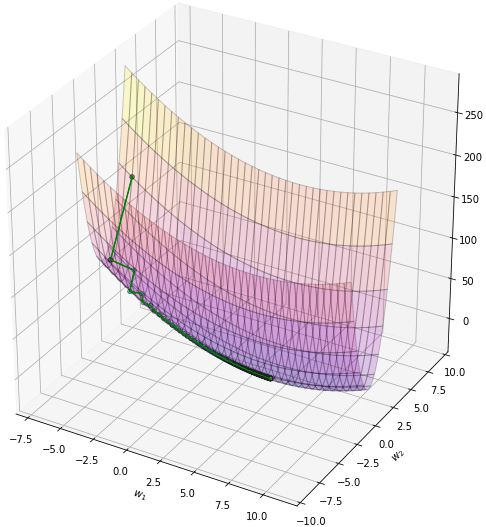
จะเห็นว่าการเคลื่อนที่ซิกแซกไปมา ไม่มุ่งตรงดิ่งสู่เป้าหมาย เพราะทิศทางการเคลื่อนที่เป็นไปตามความชันอย่างเดียว พอโดดข้ามไปอีกฝั่งความชันเปลี่ยนกะทันหันก็เด้งกลับ อีกทั้งช่วงท้ายๆจะช้า
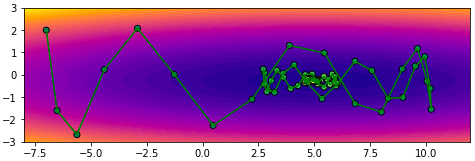
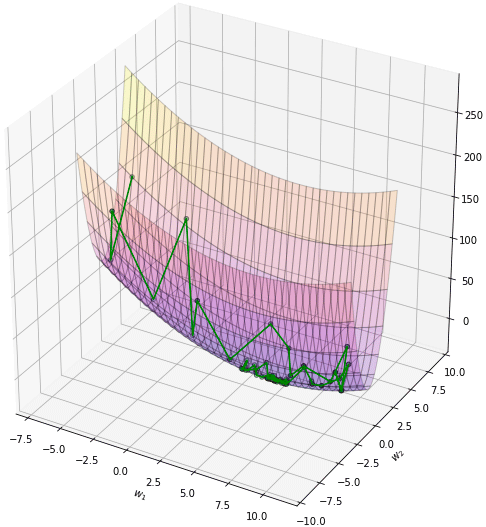
จากนั้นลองสร้างฟังก์ชันสำหรับวิธีการที่ใช้โมเมนตัม โดยเพิ่มพจน์โมเมนตัมลงไป จะได้ดังนี้ (mmtsgd ในที่นี้ย่อมาจาก momentum SGD)
จะเห็นว่าพอเพิ่มโมเมนตัมเข้าไปโดยที่อัตราการเรียนรู้ยังเท่าเดิมอยู่จะทำให้เคลื่อนที่ไปเยอะกว่า แต่ไปๆมาๆสุดท้ายแล้วก็จะลู่เข้า
โดยทั่วไปควรปรับอัตราการเรียนรู้ให้ลดลงไปกว่าตอนที่ไม่ใช้โมเมนตัม เช่นลองปรับเหลือ 0.004 ผลที่ได้จะออกมาแบบนี้ เคลื่อนที่เข้าสู่คำตอบอย่างสวยงาม
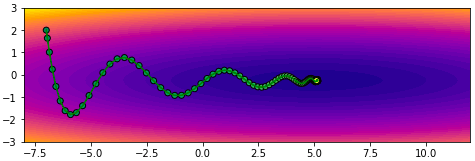
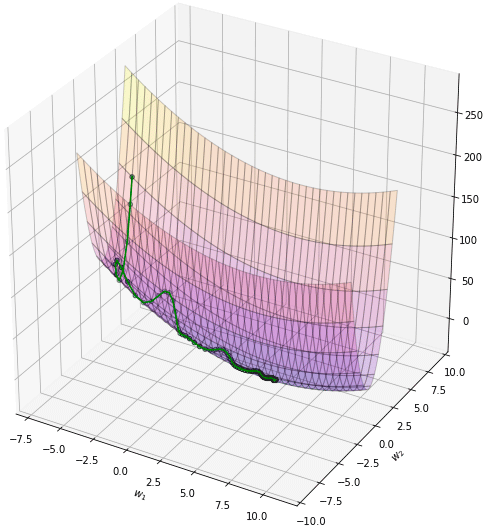
การเคลื่อนที่ไม่เปลี่ยนกะทันหันเพราะมีผลจากการเคลื่อนที่ของครั้งที่แล้วอยู่ ดูเป็นธรรมชาติและมุ่งสู่เป้าหมายได้ง่ายกว่า
ตัวอย่างที่เขียนข้างต้นนี้เป็นการเขียนให้ดูเข้าใจง่ายในกรณีพารามิเตอร์มีแค่ ๒ ตัว ในที่นี้คือ w1 และ w2
แต่ในเวลาใช้งานจริงๆจะมีพารามิเตอร์กี่ตัวก็ได้ ดังนั้นเพื่อให้เป็นรูปทั่วไปขอเขียนฟังก์ชันใหม่เป็นแบบนี้
เวลาที่ใช้ก็ใส่ค่าเป็นอาเรย์ของค่าเริ่มต้นแบบนี้
ผลที่ได้จะเหมือนกับที่เขียนตอนแรก แต่ต่อจากนี้ไปจะใช้วิธีการเขียนแบบนี้ในการแนะนำวิธีการต่อๆไป
โมเมนตัมของเนสเตรอฟ (Nesterov momentum)
วิธีการโมเมนตัมเป็นหลักการที่ใช้ได้ดี แต่ต่อมาก็มีคนเสนอว่านอกจากจะแค่เพิ่มโมเมนตัมไปแล้ว ในเมื่อรู้ว่ากำลังจะเคลื่อนที่ไปทางไหนอยู่ แบบนั้นค่าความชันที่จะเอามาคูณกับอัตราการเรียนรู้ก็ควรจะเปลี่ยนมาใช้เป็นความชันของบริเวณที่กำลังมุ่งหน้าไปด้วย
ชื่อของวิธีการนี้ได้ตั้งตามชื่อของยูรี เนสเตรอฟ (Yurii Nesterov, Юрий Нестеров) นักคณิตศาสตร์ชาวรัสเซีย บางทีก็เรียกว่าความชันแบบเร่งของเนสเตรอฟ (Nesterov Accelerated Gradient) ย่อว่า NAG
การคำนวณถูกปรับเป็นแบบนี้
..(8)
สิ่งที่ต่างกันมีแค่ว่าความชัน g⃗ ในที่นี้ไม่ใช่ความชันของตำแหน่ง w ที่อยู่ แต่เป็นความชันของตำแหน่งที่จะมุ่งไปหากเคลื่อนไปต่อตามผลของโมเมนตัม
ดังนั้นแล้วอาจเขียนฟังก์ชันใหม่ได้ดังนี้
เพียงแต่ว่าการคำนวณแบบนี้มีความยุ่งยากอยู่ตรงที่ว่าเราต้องไปคิดค่าความชันของจุดอื่นที่ไม่ใช่ตรงที่อยู่นี้ แต่ในการใช้งานจริงวิธีการหาค่าความชันไม่ได้ง่ายเหมือนอย่างในตัวอย่างนี้ หากใช้วิธีนี้จะทำให้ต้องเปลืองแรงในการคำนวณเพิ่มเติม
อย่างไรก็ตามมีวิธีคำนวณที่สะดวกกว่านั้นคือลองเปลี่ยนรูปตรงส่วนของความชันใหม่แบบนี้
..(9)
ได้สูตรคำนวณเป็นแบบนี้ออกมา คือใช้ความชันของตำแหน่งที่ผ่านมาแล้ว ไม่ต้องไปหาความชันในตำแหน่งใหม่ที่ยังไม่เคยไปถึงมาก่อนแล้ว
..(10)
ในการเขียนโค้ดเราแค่ต้องเพิ่มเติมส่วนตัวแปรที่เก็บค่าความชันของตำแหน่งที่อยู่ก่อนหน้า ในที่นี้ให้เป็น gw0
ลองใช้ดู
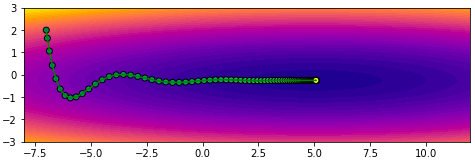
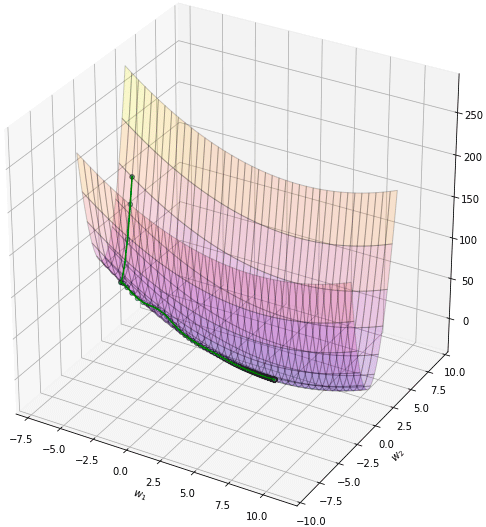
ผลที่ได้จะเห็นว่ามุ่งสู่คำตอบได้เร็วกว่าโมเมนตัมแบบเดิม
AdaGrad
นอกจากการเพิ่มพจน์โมเมนตัมเข้าไปแล้ว อีกทางเลือกหนึ่งก็คือการปรับในส่วนพจน์ของอัตราการเรียนรู้ให้เปลี่ยนแปลงลดลงตามเวลา
ในจำนวนนั้นวิธีที่พื้นฐานที่สุดก็คือ AdaGrad ย่อมาจาก Adaptive Gradient
การคำนวณเป็นตามนี้
..(11)
โดยที่ G คือผลรวมกำลังสองของความชันทั้งหมดสะสมตั้งแต่เริ่มการเรียนรู้
..(12)
ลองเขียนโค้ดดู ได้ดังนี้
1e-7 ที่ใส่เข้ามาใน G ตั้งแต่เริ่มต้นนี้เป็นแค่ค่าเล็กๆที่ใส่เข้าไปเพื่อกันกรณีที่ความชันเริ่มต้นเป็น 0 ซึ่งจะทำให้ตัวหารเป็น 0 และเกิดข้อผิดพลาดขึ้น
จากนั้นลองใช้ดู โดยปกติเวลาใช้วิธีนี้ค่าอัตราการเรียนรู้ eta ควรจะมากเมื่อเทียบกับวิธีอื่น เพราะจะลดลงอย่างรวดเร็ว
ข้อดีของวิธีนี้ก็คือไม่ต้องการไฮเพอร์พารามิเตอร์เพิ่มเติมนอกเหนือไปจาก η เลย
AdaDelta
วิธี AdaGrad มีข้อเสียตรงที่ว่ายิ่งเรียนรู้ไปเรื่อยๆเวลาผ่านไปอัตราการรู้จะยิ่งลดลงเพราะว่าค่า G ซึ่งเป็นตัวหารนั้นบวกเพิ่มขึ้นเรื่อยๆไม่มีลด ดังนั้นทำให้ช่วงหลังๆการเรียนรู้แทบจะหยุดนิ่ง
วิธีการที่ถูกคิดมาทดแทนเพื่อแก้ปัญหาของ AdaGrad มีหลายวิธี หนึ่งในนั้นก็คือ AdaDelta
ทำโดยแค่ดัดแปลงค่า G นิดหน่อย จากที่เดิมทีบวกไปเรื่อยๆ คราวนี้ปรับกลายเป็นแบบนี้
..(13)
โดยที่ค่า ρ เป็นพารามิเตอร์อีกตัวที่ต้องกำหนด มีค่าระหว่าง 0 ถึง 1
เขียนโค้ดแล้วใช้ดู
RMSprop
วิธีนี้คล้ายกับ Adadelta คือปรับปรุงจาก AdaGrad เป็นวิธีที่คิดขึ้นโดยอาจารย์ที่สอนในบทเรียนออนไลน์เว็บ coursera
Adam
เป็นอีกวิธีที่ปรับปรุงมาจาก AdaGrad โดยนำเอาหลักของโมเมนตัมมารวมอยู่ในนั้นด้วย ชื่อย่อมาจาก Adaptive Moment
สูตรการคำนวณเป็นดังนี้
..(14)
..(15)
..(16)
มีไฮเพอร์พารามิเตอร์ที่ต้องกำหนดเพิ่มนอกจาก η ก็คือ β1 และ β2 ปกติแล้วจะให้ β1=0.9 และ β2=0.999
วิธีนี้แม้จะดูแล้วซับซ้อนกว่าอันอื่น แต่สำหรับตอนนี้ถือเป็นวิธีที่ค่อนข้างได้รับการตอบรับดีมาก ถ้ายังลังเลว่าควรจะใช้อะไรก็อาจเริ่มลองจาก Adam ก่อนได้ เพียงแต่ว่าวิธีไหนดีสุดนั้นขึ้นกับปัญหา ดังนั้นก็อาจยังจำเป็นต้องลองดูหลายวิธี
ลองเขียนโค้ดใช้งานดู
เปรียบเทียบ
สุดท้ายลองดูภาพเปรียบเทียบวิธีต่างๆซึ่งมีคนทำเอาไว้ (ที่มา http://img.blog.csdn.net/20160824161755284)
ส่วนภาพนี้เปรียบเทียบสถานการณ์ที่เจอพื้นรูปอานม้า (ที่มา http://img.blog.csdn.net/20160824161815758)
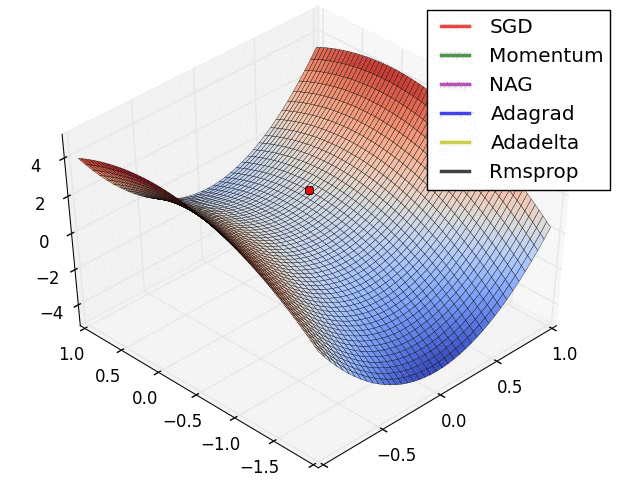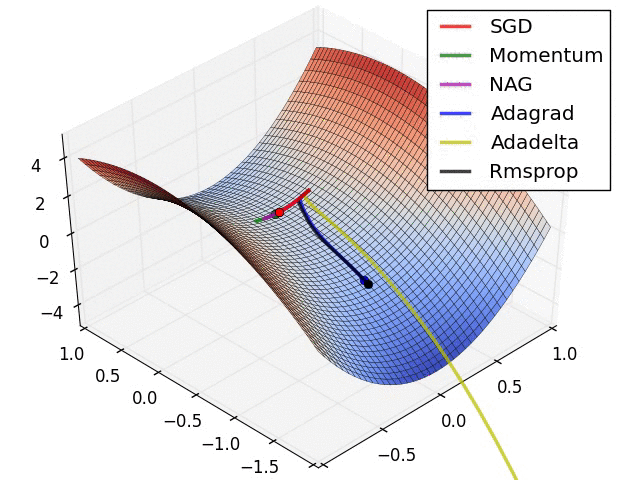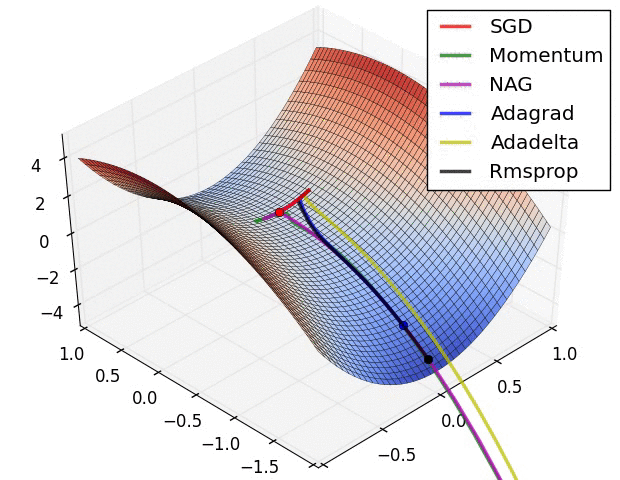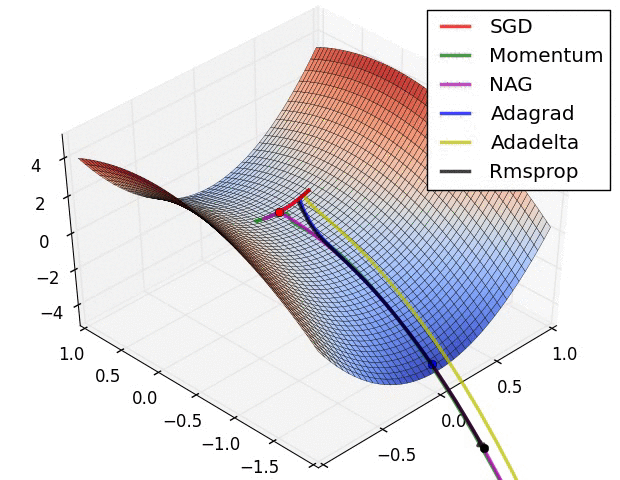
แต่ทั้งนี้ประสิทธิภาพของแต่ละวิธีก็ขึ้นอยู่กับไฮเพอร์พารามิเตอร์ต่างๆซึ่งต้องเลือกใช้ให้เหมาะสมด้วย
ทำเป็นคลาสเพื่อนำมาใช้ในการเรียนรู้ของเครื่อง
หลังจากที่ได้อธิบายหลักการของวิธีต่างๆไปแล้วข้างต้น คราวนี้เราจะมาลองใส่ลงไปในคลาสของแบบจำลองการเรียนรู้ของเครื่องเพื่อใช้งานจริง
วิธีการในการต่างๆที่ใช้เป็นเครื่องมือในการเคลื่อนลงตามความชันแบบต่างๆเหล่านี้ถูกเรียกว่าออปทิไมเซอร์ (optimizer) แปลว่าเครื่องมือที่จะปรับให้อะไรบางอย่างออกมาดีหรือเหมาะที่สุด
วิธีการใช้งานที่สะดวกก็คือให้สร้างคลาสใหม่สำหรับออปทิไมเซอร์เหล่านี้ จากนั้นก็เรียกใช้งานในภายในคลาสของแบบจำลองการเรียนรู้ของเครื่องอีกที
อาจดูซับซ้อนสักหน่อยแต่ทำแบบนี้แล้วสะดวกในการใช้งานมาก
ตัวอย่างการสร้างคลาสด้วยวิธีต่างๆที่แนะนำมา เริ่มจาก ๓ อย่างแรก SGD, โมเมนตัม และ NAG
เวลาใช้ก็เริ่มจากสร้างออบเจ็กต์ของตัวออปทิไมเซอร์ที่ต้องการขึ้นมาอันหนึ่ง __init__ ในที่นี้จะสร้างค่าเริ่มต้นจากไฮเพอร์พารามิเตอร์ (อัตราการเรียนรู้, โมเมนตัม, ฯลฯ) ที่ป้อนเข้ามา
จากนั้นสร้างเมธอด __call__ ไว้ สำหรับเรียกใช้เมื่อมีการวนซ้ำ การทำงานในส่วนนี้คือปรับค่าพารามิเตอร์น้ำหนักที่ถูกป้อนเข้ามาทุกครั้งที่มีการเรียกใช้ พร้อมกันนั้นก็มีการบันทึกค่าซึ่งจะต้องนำกลับมาใช้ในการคำนวณครั้งต่อไปด้วย เช่นค่าความเปลี่ยนแปลงของรอบที่แล้ว ซึ่งต้องใช้คำนวณโมเมนตัม รวมถึงค่าความชันของรอบก่อนหน้าซึ่งต้องใช้ในโมเมนตัมแบบเนสเตรอฟ
อนึ่ง ในส่วนบรรทัดสุดท้ายที่ปรับค่า w นั้นจำเป็นต้องใช้เป็น w += self.dw ไม่ใช่ w = w+ self.dw ดูเผินๆจะคิดว่าเหมือนกัน แต่หากใช้อย่างหลัง w จะกลายเป็นสร้างอาเรย์ใหม่ขึ้นแต่อาเรย์เดิมจะไม่มีการปรับค่า ตรงนี้เป็นเกร็ดเล็กน้อย เป็นเรื่องปลีกย่อยสำหรับพฤติกรรมของ ndarray
ลองดูตัวอย่างการใช้ พอนิยามคลาสแล้วเราจะเขียนใหม่ได้ดังนี้เพื่อให้ได้ผลเหมือนกับวิธีที่ทำตอนแรก
ในที่นี้ opt ถูกสร้างมาเป็นออบเจ็กต์ในคลาส Nag จากนั้นพอเข้าสู่วังวน for โดยที่ทุกรอบจะมีการเรียกใช้ opt ซึ่งจะทำสิ่งที่อยู่ในเมธอด __call__ ที่นิยามไว้ ผลก็คือตัวแปร w เปลี่ยนค่าไปเรื่อยๆทุกครั้ง เข้าใกล้จุดต่ำสุดไปเรื่อยๆ
ดูเผินๆอาจมองว่าทำเป็นคลาสแล้วยุ่งยากกว่าเดิม แต่ว่าแบบนี้เหมาะกับการนำมาใช้งานจริง
ต่อมาสำหรับคลาสของออปทิไมเซอร์ตระกูล Ada ทั้งหลายนิยามดังนี้
จากนั้นตรงนี้จะเป็นตัวอย่างในการสร้างคลาสถดถอยโลจิสติกที่สามารถตั้งให้ใช้ออปทิไมเซอร์เหล่านี้ตามที่ต้องการได้
คลาสที่จะเขียนต่อไปนี้มีพื้นฐานจากคลาส ThotthoiLogistic ในหน้า https://phyblas.hinaboshi.com/20161228
แต่เอามาปรับปรุงโดยเปลี่ยนส่วนนิยามคลาสจากที่เดิมตอนสร้างใส่ค่าอัตราการเรียนรู้ (eta) เป็นมาใส่ออปทิไมเซอร์ (opt) แทน
จากนั้นลองดูตัวอย่างการใช้งาน โดยลองสร้างข้อมูลเป็นกลุ่มก้อน จากนั้นใช้ AdaGrad ในการเรียนรู้ (รายละเอียดของ datasets.make_blobs https://phyblas.hinaboshi.com/20161127)
ผลที่ได้ก็สามารถแบ่งข้อมูลออกมาได้แบบนี้
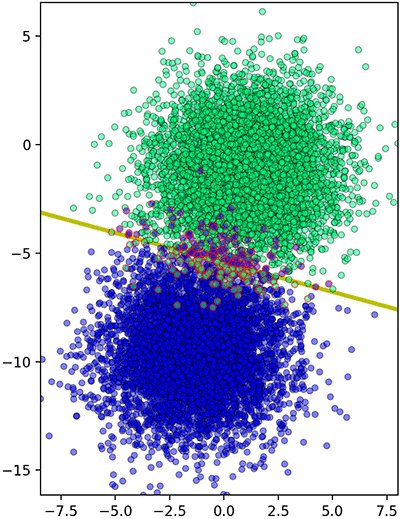
สุดท้าย ลองมาสร้างกราฟแสดงความคืบหน้าในการเรียนรู้เปรียบเทียบวิธีต่างๆกันดู
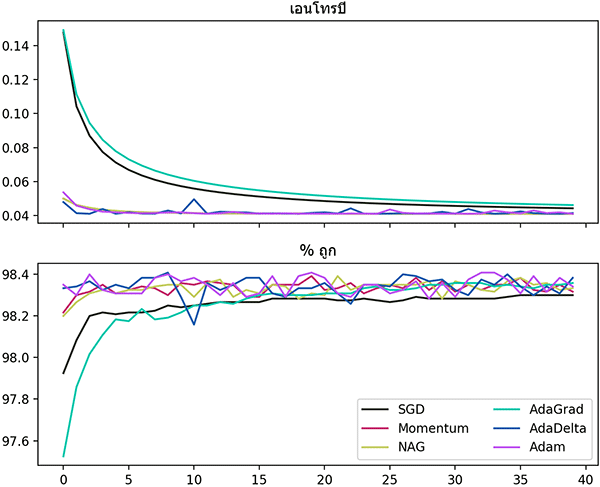
อย่างไรก็ตาม กราฟนี้ได้แค่เปรียบเทียบว่าหากอัตราการเรียนรู้เท่ากันจะเป็นยังไงเท่านั้น ไม่อาจบอกได้ว่าวิธีไหนดีกว่า
เวลาไหนควรใช้วิธีไหนดีที่สุดนั้นยังเป็นเรื่องที่ต้องทำวิจัยกันต่อไป
อ้างอิง
รายละเอียดได้เขียนถึงเอาไว้ตั้งแต่บทความช่วงแรก https://phyblas.hinaboshi.com/20161210
ในการเคลื่อนลงตามความชันแบบธรรมดานั้นโดยพื้นฐานแล้วการเปลี่ยนแปลงค่าของพารามิเตอร์จะขึ้นกับอัตราการเรียนรู้ (学习率, learning rate) ล้วนๆ ซึ่งอัตราการเรียนรู้นี้จะคงที่ตลอดไม่ว่าจะวนซ้ำเพื่อฝึกไปกี่ครั้ง
การที่อัตราการเรียนรู้คงที่นั้นเป็นวิธีการที่เป็นเบื้องต้นเรียบง่าย แต่ต่อมาก็ได้มีคนพยายามจะปรับปรุงหาวิธีทำให้การปรับค่าพารามิเตอร์ขึ้นกับปัจจัยต่างๆมากขึ้น
ในที่นี้จะแนะนำวิธีหลักๆที่คนนิยมใช้กันอยู่ตอนนี้ ได้แก่ โมเมนตัม, NAG, AdaGrad, AdaDelta, RMSprop, Adam
โมเมนตัม (momentum)
โมเมนตัมคือปริมาณที่บอกสภาพการเคลื่อนที่ของวัตถุ ปกติเราจะคุ้นกับโมเมนตัมในทางฟิสิกส์ เวลาของกลิ้งตกจากที่สูงลงที่ต่ำมันไม่ได้เคลื่อนลงในทิศเดียวกับความชันเสียทีเดียว ปกติแล้วสิ่งที่กำลังเคลื่อนที่จะมีความเฉื่อย ต่อให้มีแรงมากระทำในทิศทางอื่นแต่มันก็จะยังคงจะเคลื่อนที่ต่อไปในทางเดิมอยู่
สำหรับโมเมนตัมที่ใช้ในวิธีการเคลื่อนลงตามความชันในที่นี้ก็มีหลักการคล้ายๆกัน คือสร้างผลที่เสมือนกับการเคลื่อนที่ของวัตถุที่มีความเฉื่อยเข้ามา
หากใส่โมเมนตัมเข้าไป เวลาคำนวนตำแหน่งต่อไปจะมีผลจากการเคลื่อนไหวในขั้นก่อนหน้านี้มาเกี่ยวด้วย โดยจะพยายามรักษาทิศการเคลื่อนที่ในแนวเดิม
จากที่เดิมทีค่าใหม่จะขึ้นกับความชันและอัตราการเรียนรู้เท่านั้น คือ
..(1)
ในที่นี้ w คือพารามิเตอร์น้ำหนักที่ต้องการปรับ η คืออัตราการเรียนรู้ ส่วน t คือเลขที่บอกว่าเป็นขั้นที่เท่าไหร่
สัญลักษณ์เว็กเตอร์ในที่นี้แสดงว่าเป็นปริมาณที่มีหลายมิติ เช่นค่าพารามิเตอร์น้ำหนัก w⃗ ก็แบ่งเป็น w1,w2,... ถ้าเป็นในโปรแกรมก็คือเป็นตัวแปรที่เป็นอาเรย์นั่นเอง
ส่วน g⃗ คืออนุพันธ์ย่อย (ก็คือความชัน) ของฟังก์ชันค่าเสียหาย J ที่ตำแหน่ง wt
..(2)
ค่าน้ำหนักในขั้นนี้ตอนต่อไปจะเปลี่ยนแปลงไป Δw นั่นคือ
..(3)
ทีนี้ต่อหากเพิ่มโมเมนตัมเข้าไป สมการ (1) จะกลายเป็นแบบนี้
..(4)
ที่เพิ่มเข้ามาคือพจน์ αΔw⃗t โดย α ในที่นี้คือขนาดของโมเมนตัม ค่าที่มักจะใช้กันคือ 0.9 ถ้าหากพจน์นี้เป็น 0 ก็จะเท่ากับการเคลื่อนลงตามความชันธรรมดาที่ไม่มีโมเมนตัม
จากสมการจะเห็นได้ว่าพจน์ที่เพิ่มเข้ามาจะช่วยให้การเปลี่ยนแปลงจากขั้นที่แล้วยังมีผลอยู่ด้วย นั่นเท่ากับเป็นการพยายามรักษาการเคลื่อนที่ ดังนั้นเส้นทางการเคลื่อนที่จะดูคล้ายกับวัตถุจริงมากขึ้น
เมื่อเพิ่มมาแล้วผลจะเป็นยังไงลองมาสร้างตัวอย่างขึ้นแล้วเพื่อเปรียบเทียบผลที่ได้กันดู
สมมุติว่าฟังก์ชันค่าเสียหายขึ้นกับตัวแปรสองตัวเป็นดังนี้
..(5)
หาอนุพันธ์ได้ดังนี้
..(6)
..(7)
ลองเขียนเป็นฟังก์ชันในไพธอนได้ดังนี้
def J(w1,w2):
return 0.5*w1**2 + 20*w2**2 - 5*w1 + 10*w2 - 7
def dJ(w1,w2):
return w1 - 5, 40*w2 + 10จากค่าความชันที่ได้คงดูออกได้ไม่ยากว่าจุดต่ำสุดควรอยู่ที่จุด (5,-0.25) นี่คือเป้าหมายที่ต้องการมุ่งไปให้ถึง
ลองตั้งจุดเริ่มต้นสักจุด ในที่นี้ลองเริ่มจาก (-7,2) แล้วก็เริ่มปรับค่าโดยวิธีเคลื่อนลงตามความชันแบบธรรมดาจะเป็นแบบนี้
def sgd(w1,w2,n,eta=0.01):
w1_,w2_ = [w1],[w2]
for i in range(n):
gw1,gw2 = dJ(w1,w2)
dw1 = -eta*gw1
dw2 = -eta*gw2
w1 = w1+dw1
w2 = w2+dw2
w1_.append(w1)
w2_.append(w2)
return w1_,w2_
w1,w2 = -7.,2.
w1_,w2_ = sgd(w1,w2,n=50,eta=0.04)
# วาดกราฟทั้งสองและสามมิติ
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def plot(x,y):
z = J(x,y)
mx,my = np.meshgrid(np.arange(-8,12,0.01),np.arange(-3,3,0.01))
mz = J(mx,my)
plt.figure(figsize=[8,6])
plt.plot(x,y,'g')
plt.scatter(x,y,c=np.linspace(0,1,len(x)),cmap='summer',edgecolor='k',zorder=2)
plt.contourf(mx,my,mz,40,cmap='plasma')
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlabel='$w_1$',ylabel='$w_2$',xlim=[-8,12],ylim=[-10,10])
ax.plot(x,y,z,c='g')
ax.scatter(x,y,z,c=np.linspace(0,1,len(x)),cmap='summer',edgecolor='k')
ax.plot_surface(mx,my,mz,cstride=50,rstride=50,alpha=0.2,cmap='plasma',edgecolor='k')
plt.show()
plot(np.array(w1_),np.array(w2_))

จะเห็นว่าการเคลื่อนที่ซิกแซกไปมา ไม่มุ่งตรงดิ่งสู่เป้าหมาย เพราะทิศทางการเคลื่อนที่เป็นไปตามความชันอย่างเดียว พอโดดข้ามไปอีกฝั่งความชันเปลี่ยนกะทันหันก็เด้งกลับ อีกทั้งช่วงท้ายๆจะช้า
จากนั้นลองสร้างฟังก์ชันสำหรับวิธีการที่ใช้โมเมนตัม โดยเพิ่มพจน์โมเมนตัมลงไป จะได้ดังนี้ (mmtsgd ในที่นี้ย่อมาจาก momentum SGD)
def mmtsgd(w1,w2,n,eta=0.01,mmt=0.9):
dw1,dw2 = 0,0
w1_,w2_ = [w1],[w2]
for i in range(n):
gw1,gw2 = dJ(w1,w2)
dw1 = mmt*dw1-eta*gw1
dw2 = mmt*dw2-eta*gw2
w1 = w1+dw1
w2 = w2+dw2
w1_.append(w1)
w2_.append(w2)
return w1_,w2_
w1_,w2_ = mmtsgd(w1,w2,n=100,eta=0.04)
plot(np.array(w1_),np.array(w2_))จะเห็นว่าพอเพิ่มโมเมนตัมเข้าไปโดยที่อัตราการเรียนรู้ยังเท่าเดิมอยู่จะทำให้เคลื่อนที่ไปเยอะกว่า แต่ไปๆมาๆสุดท้ายแล้วก็จะลู่เข้า


โดยทั่วไปควรปรับอัตราการเรียนรู้ให้ลดลงไปกว่าตอนที่ไม่ใช้โมเมนตัม เช่นลองปรับเหลือ 0.004 ผลที่ได้จะออกมาแบบนี้ เคลื่อนที่เข้าสู่คำตอบอย่างสวยงาม
w1_,w2_ = mmtsgd(w1,w2,n=100,eta=0.004)
plot(np.array(w1_),np.array(w2_))

การเคลื่อนที่ไม่เปลี่ยนกะทันหันเพราะมีผลจากการเคลื่อนที่ของครั้งที่แล้วอยู่ ดูเป็นธรรมชาติและมุ่งสู่เป้าหมายได้ง่ายกว่า
ตัวอย่างที่เขียนข้างต้นนี้เป็นการเขียนให้ดูเข้าใจง่ายในกรณีพารามิเตอร์มีแค่ ๒ ตัว ในที่นี้คือ w1 และ w2
แต่ในเวลาใช้งานจริงๆจะมีพารามิเตอร์กี่ตัวก็ได้ ดังนั้นเพื่อให้เป็นรูปทั่วไปขอเขียนฟังก์ชันใหม่เป็นแบบนี้
# ส่วนฟังก์ชันให้รับตัวแปรเป็นอาเรย์เดียวที่รวมค่าทั้งหมดที่ต้องการคำนวณรวดเดียว การคำนวณใช้ด็อตเป็นหลัก
def J(w):
return -7+w.dot(np.array([-5,10]))+(w**2).dot(np.array([0.5,20]))
def dJ(w):
return np.array([-5,10])+w.dot(np.array([[1,0],[0,40]]))
# ส่วนนิยามฟังก์ชันของวิธีการทั้ง ๒
def sgd(w,n,eta=0.01):
w_ = [w]
for i in range(n):
w = w-eta*dJ(w)
w_.append(w)
return np.stack(w_)
def mmtsgd(w,n,eta=0.01,mmt=0.9):
dw = w*0
w_ = [w]
for i in range(n):
gw = dJ(w)
dw = mmt*dw-eta*gw
w = w+dw
w_.append(w)
return np.stack(w_)
# ส่วนวาดกราฟ
def plot(X):
z = J(X)
mX = np.stack(np.meshgrid(np.arange(-8,12,0.01),np.arange(-3,3,0.01)),2)
mz = J(mX)
plt.figure(figsize=[8,4])
plt.axes(aspect=1)
plt.plot(X[:,0],X[:,1],'g')
plt.scatter(X[:,0],X[:,1],c=np.linspace(0,1,len(X)),cmap='summer',edgecolor='k',zorder=2)
plt.contourf(mX[:,:,0],mX[:,:,1],mz,40,cmap='plasma')
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d',xlabel='$w_1$',ylabel='$w_2$',xlim=[-8,12],ylim=[-10,10])
ax.plot(X[:,0],X[:,1],z,c='g')
ax.scatter(X[:,0],X[:,1],z,c=np.linspace(0,1,len(X)),cmap='summer',edgecolor='k')
ax.plot_surface(mX[:,:,0],mX[:,:,1],mz,cstride=50,rstride=50,alpha=0.2,cmap='plasma',edgecolor='k')
plt.show()เวลาที่ใช้ก็ใส่ค่าเป็นอาเรย์ของค่าเริ่มต้นแบบนี้
w = np.array([-7.,2.])
#w_ = sgd(w,n=100,eta=0.04)
w_ = mmtsgd(w,n=100,eta=0.004)
plot(w_)ผลที่ได้จะเหมือนกับที่เขียนตอนแรก แต่ต่อจากนี้ไปจะใช้วิธีการเขียนแบบนี้ในการแนะนำวิธีการต่อๆไป
โมเมนตัมของเนสเตรอฟ (Nesterov momentum)
วิธีการโมเมนตัมเป็นหลักการที่ใช้ได้ดี แต่ต่อมาก็มีคนเสนอว่านอกจากจะแค่เพิ่มโมเมนตัมไปแล้ว ในเมื่อรู้ว่ากำลังจะเคลื่อนที่ไปทางไหนอยู่ แบบนั้นค่าความชันที่จะเอามาคูณกับอัตราการเรียนรู้ก็ควรจะเปลี่ยนมาใช้เป็นความชันของบริเวณที่กำลังมุ่งหน้าไปด้วย
ชื่อของวิธีการนี้ได้ตั้งตามชื่อของยูรี เนสเตรอฟ (Yurii Nesterov, Юрий Нестеров) นักคณิตศาสตร์ชาวรัสเซีย บางทีก็เรียกว่าความชันแบบเร่งของเนสเตรอฟ (Nesterov Accelerated Gradient) ย่อว่า NAG
การคำนวณถูกปรับเป็นแบบนี้
..(8)
สิ่งที่ต่างกันมีแค่ว่าความชัน g⃗ ในที่นี้ไม่ใช่ความชันของตำแหน่ง w ที่อยู่ แต่เป็นความชันของตำแหน่งที่จะมุ่งไปหากเคลื่อนไปต่อตามผลของโมเมนตัม
ดังนั้นแล้วอาจเขียนฟังก์ชันใหม่ได้ดังนี้
def nag(w,n,eta=0.01,mmt=0.9):
dw = w*0
w_ = [w]
for i in range(n):
g_ = dJ(w+mmt*dw)
dw = mmt*dw-eta*g_
w = w+dw
w_.append(w)
return np.stack(w_)เพียงแต่ว่าการคำนวณแบบนี้มีความยุ่งยากอยู่ตรงที่ว่าเราต้องไปคิดค่าความชันของจุดอื่นที่ไม่ใช่ตรงที่อยู่นี้ แต่ในการใช้งานจริงวิธีการหาค่าความชันไม่ได้ง่ายเหมือนอย่างในตัวอย่างนี้ หากใช้วิธีนี้จะทำให้ต้องเปลืองแรงในการคำนวณเพิ่มเติม
อย่างไรก็ตามมีวิธีคำนวณที่สะดวกกว่านั้นคือลองเปลี่ยนรูปตรงส่วนของความชันใหม่แบบนี้
..(9)
ได้สูตรคำนวณเป็นแบบนี้ออกมา คือใช้ความชันของตำแหน่งที่ผ่านมาแล้ว ไม่ต้องไปหาความชันในตำแหน่งใหม่ที่ยังไม่เคยไปถึงมาก่อนแล้ว
..(10)
ในการเขียนโค้ดเราแค่ต้องเพิ่มเติมส่วนตัวแปรที่เก็บค่าความชันของตำแหน่งที่อยู่ก่อนหน้า ในที่นี้ให้เป็น gw0
def nag(w,n,eta=0.01,mmt=0.9):
dw = w*0
gw0 = dJ(w)
w_ = [w]
for i in range(n):
gw = dJ(w)
dw = mmt*dw-eta*(gw+mmt*(gw-gw0))
w = w+dw
gw0 = gw
w_.append(w)
return np.stack(w_)ลองใช้ดู
plot(nag(np.array([-7.,2.]),n=100,eta=0.004))

ผลที่ได้จะเห็นว่ามุ่งสู่คำตอบได้เร็วกว่าโมเมนตัมแบบเดิม
AdaGrad
นอกจากการเพิ่มพจน์โมเมนตัมเข้าไปแล้ว อีกทางเลือกหนึ่งก็คือการปรับในส่วนพจน์ของอัตราการเรียนรู้ให้เปลี่ยนแปลงลดลงตามเวลา
ในจำนวนนั้นวิธีที่พื้นฐานที่สุดก็คือ AdaGrad ย่อมาจาก Adaptive Gradient
การคำนวณเป็นตามนี้
..(11)
โดยที่ G คือผลรวมกำลังสองของความชันทั้งหมดสะสมตั้งแต่เริ่มการเรียนรู้
..(12)
ลองเขียนโค้ดดู ได้ดังนี้
def adagrad(w,n,eta=0.01):
G = 1e-7
w_ = [w]
for i in range(n):
gw = dJ(w)
G += gw**2
dw = -eta*gw/np.sqrt(G)
w = w+dw
w_.append(w)
return np.stack(w_)1e-7 ที่ใส่เข้ามาใน G ตั้งแต่เริ่มต้นนี้เป็นแค่ค่าเล็กๆที่ใส่เข้าไปเพื่อกันกรณีที่ความชันเริ่มต้นเป็น 0 ซึ่งจะทำให้ตัวหารเป็น 0 และเกิดข้อผิดพลาดขึ้น
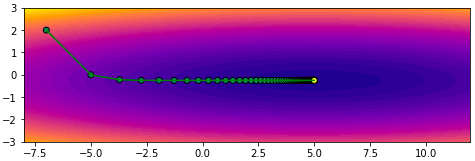
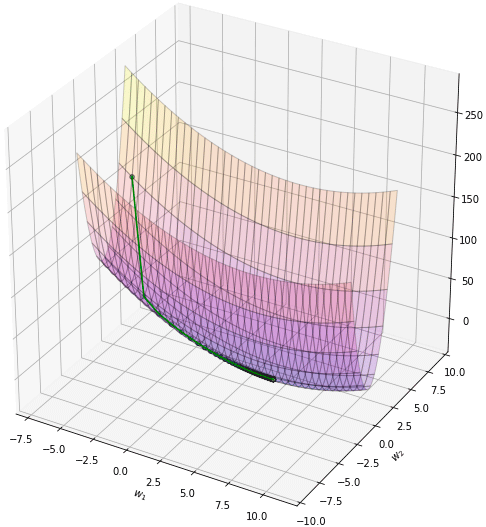
จากนั้นลองใช้ดู โดยปกติเวลาใช้วิธีนี้ค่าอัตราการเรียนรู้ eta ควรจะมากเมื่อเทียบกับวิธีอื่น เพราะจะลดลงอย่างรวดเร็ว
plot(adagrad(np.array([-7.,2.]),n=100,eta=2))

ข้อดีของวิธีนี้ก็คือไม่ต้องการไฮเพอร์พารามิเตอร์เพิ่มเติมนอกเหนือไปจาก η เลย
AdaDelta
วิธี AdaGrad มีข้อเสียตรงที่ว่ายิ่งเรียนรู้ไปเรื่อยๆเวลาผ่านไปอัตราการรู้จะยิ่งลดลงเพราะว่าค่า G ซึ่งเป็นตัวหารนั้นบวกเพิ่มขึ้นเรื่อยๆไม่มีลด ดังนั้นทำให้ช่วงหลังๆการเรียนรู้แทบจะหยุดนิ่ง
วิธีการที่ถูกคิดมาทดแทนเพื่อแก้ปัญหาของ AdaGrad มีหลายวิธี หนึ่งในนั้นก็คือ AdaDelta
ทำโดยแค่ดัดแปลงค่า G นิดหน่อย จากที่เดิมทีบวกไปเรื่อยๆ คราวนี้ปรับกลายเป็นแบบนี้
..(13)
โดยที่ค่า ρ เป็นพารามิเตอร์อีกตัวที่ต้องกำหนด มีค่าระหว่าง 0 ถึง 1
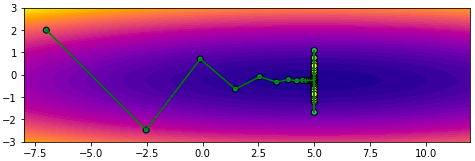
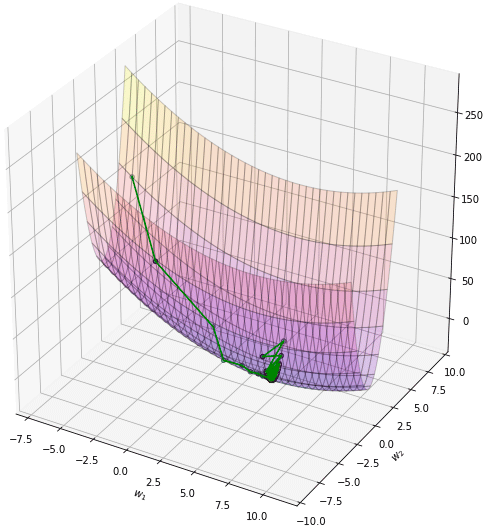
เขียนโค้ดแล้วใช้ดู
def adadelta(w,n,eta=1.,rho=0.95):
G = 1e-7
w_ = [w]
for i in range(n):
gw = dJ(w)
G = rho*G+(1-rho)*gw**2
dw = -eta*gw/np.sqrt(G)
w = w+dw
w_.append(w)
return np.stack(w_)
plot(adadelta(np.array([-7.,2.]),n=100,eta=1))

RMSprop
วิธีนี้คล้ายกับ Adadelta คือปรับปรุงจาก AdaGrad เป็นวิธีที่คิดขึ้นโดยอาจารย์ที่สอนในบทเรียนออนไลน์เว็บ coursera
Adam
เป็นอีกวิธีที่ปรับปรุงมาจาก AdaGrad โดยนำเอาหลักของโมเมนตัมมารวมอยู่ในนั้นด้วย ชื่อย่อมาจาก Adaptive Moment
สูตรการคำนวณเป็นดังนี้
..(14)
..(15)
..(16)
มีไฮเพอร์พารามิเตอร์ที่ต้องกำหนดเพิ่มนอกจาก η ก็คือ β1 และ β2 ปกติแล้วจะให้ β1=0.9 และ β2=0.999
วิธีนี้แม้จะดูแล้วซับซ้อนกว่าอันอื่น แต่สำหรับตอนนี้ถือเป็นวิธีที่ค่อนข้างได้รับการตอบรับดีมาก ถ้ายังลังเลว่าควรจะใช้อะไรก็อาจเริ่มลองจาก Adam ก่อนได้ เพียงแต่ว่าวิธีไหนดีสุดนั้นขึ้นกับปัญหา ดังนั้นก็อาจยังจำเป็นต้องลองดูหลายวิธี
ลองเขียนโค้ดใช้งานดู
def adam(w,n,eta=0.001,beta1=0.9,beta2=0.999):
m = w*0.
v = m+1e-7
w_ = [w]
for i in range(1,n+1):
gw = dJ(w)
m = beta1*m+(1-beta1)*gw
v = beta2*v+(1-beta2)*gw**2
dw = -eta*np.sqrt(1-beta2**i)/(1-beta1**i)*m/np.sqrt(v)
w = w+dw
w_.append(w)
return np.stack(w_)
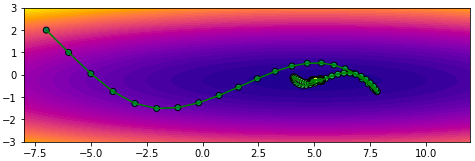
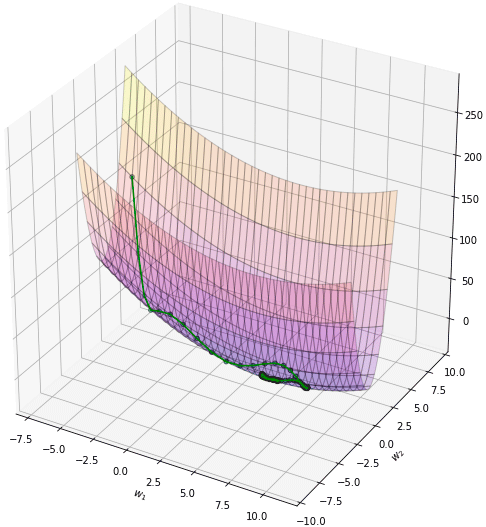
plot(adam(np.array([-7.,2.]),n=100,eta=1))

เปรียบเทียบ
สุดท้ายลองดูภาพเปรียบเทียบวิธีต่างๆซึ่งมีคนทำเอาไว้ (ที่มา http://img.blog.csdn.net/20160824161755284)

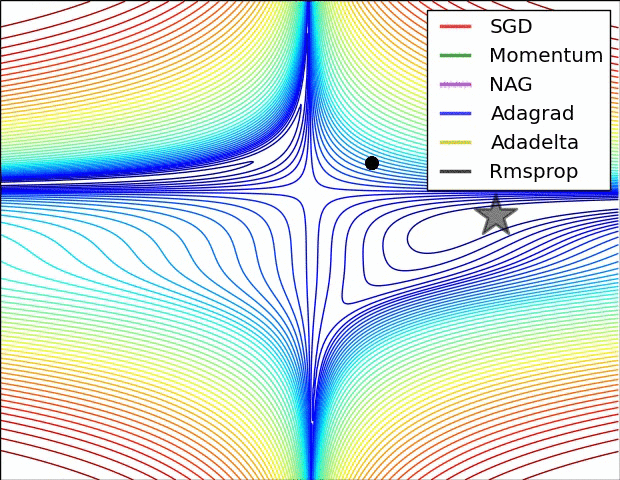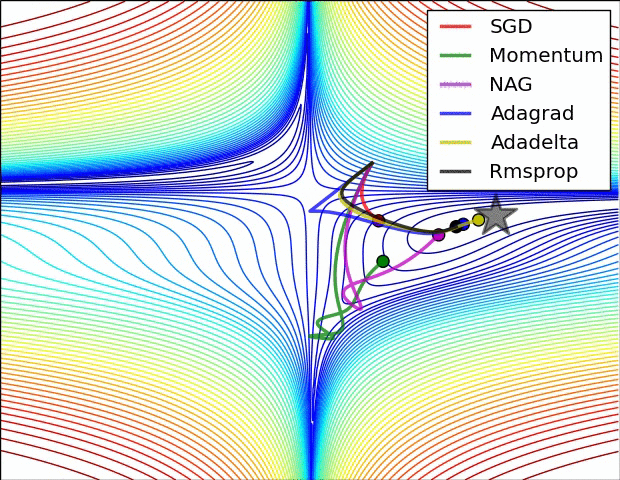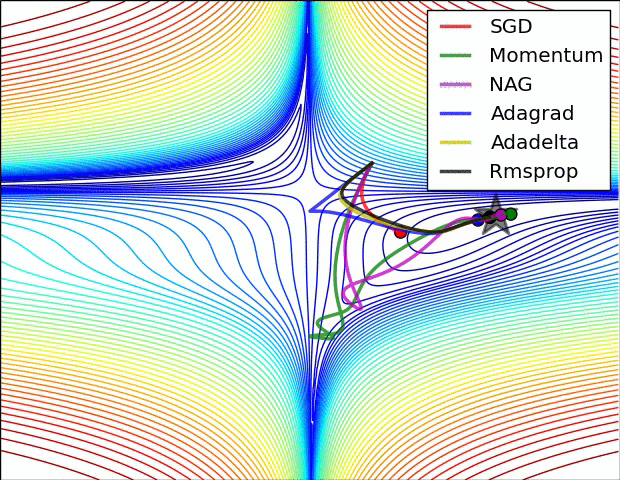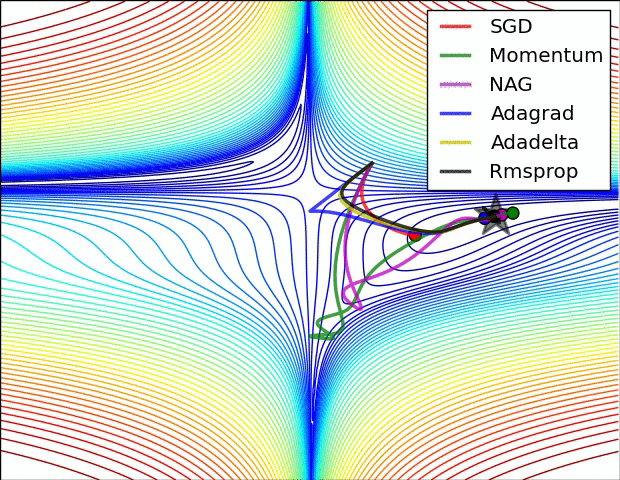
ส่วนภาพนี้เปรียบเทียบสถานการณ์ที่เจอพื้นรูปอานม้า (ที่มา http://img.blog.csdn.net/20160824161815758)

แต่ทั้งนี้ประสิทธิภาพของแต่ละวิธีก็ขึ้นอยู่กับไฮเพอร์พารามิเตอร์ต่างๆซึ่งต้องเลือกใช้ให้เหมาะสมด้วย
ทำเป็นคลาสเพื่อนำมาใช้ในการเรียนรู้ของเครื่อง
หลังจากที่ได้อธิบายหลักการของวิธีต่างๆไปแล้วข้างต้น คราวนี้เราจะมาลองใส่ลงไปในคลาสของแบบจำลองการเรียนรู้ของเครื่องเพื่อใช้งานจริง
วิธีการในการต่างๆที่ใช้เป็นเครื่องมือในการเคลื่อนลงตามความชันแบบต่างๆเหล่านี้ถูกเรียกว่าออปทิไมเซอร์ (optimizer) แปลว่าเครื่องมือที่จะปรับให้อะไรบางอย่างออกมาดีหรือเหมาะที่สุด
วิธีการใช้งานที่สะดวกก็คือให้สร้างคลาสใหม่สำหรับออปทิไมเซอร์เหล่านี้ จากนั้นก็เรียกใช้งานในภายในคลาสของแบบจำลองการเรียนรู้ของเครื่องอีกที
อาจดูซับซ้อนสักหน่อยแต่ทำแบบนี้แล้วสะดวกในการใช้งานมาก
ตัวอย่างการสร้างคลาสด้วยวิธีต่างๆที่แนะนำมา เริ่มจาก ๓ อย่างแรก SGD, โมเมนตัม และ NAG
class Sgd:
def __init__(self,eta=0.01):
self.eta = eta
def __call__(self,w,g):
w += -self.eta*g
class Mmtsgd:
def __init__(self,eta=0.01,mmt=0.9):
self.eta = eta
self.mmt = mmt
self.dw = 0
def __call__(self,w,gw):
self.dw = self.mmt*self.dw-self.eta*gw
w += self.dw
class Nag:
def __init__(self,eta=0.01,mmt=0.9):
self.eta = eta
self.mmt = mmt
self.dw = 0
self.gw0 = np.nan
def __call__(self,w,gw):
if(self.gw0 is np.nan):
self.gw0 = gw
self.dw = self.mmt*self.dw-self.eta*(gw+self.mmt*(gw-self.gw0))
self.gw0 = gw
w += self.dwเวลาใช้ก็เริ่มจากสร้างออบเจ็กต์ของตัวออปทิไมเซอร์ที่ต้องการขึ้นมาอันหนึ่ง __init__ ในที่นี้จะสร้างค่าเริ่มต้นจากไฮเพอร์พารามิเตอร์ (อัตราการเรียนรู้, โมเมนตัม, ฯลฯ) ที่ป้อนเข้ามา
จากนั้นสร้างเมธอด __call__ ไว้ สำหรับเรียกใช้เมื่อมีการวนซ้ำ การทำงานในส่วนนี้คือปรับค่าพารามิเตอร์น้ำหนักที่ถูกป้อนเข้ามาทุกครั้งที่มีการเรียกใช้ พร้อมกันนั้นก็มีการบันทึกค่าซึ่งจะต้องนำกลับมาใช้ในการคำนวณครั้งต่อไปด้วย เช่นค่าความเปลี่ยนแปลงของรอบที่แล้ว ซึ่งต้องใช้คำนวณโมเมนตัม รวมถึงค่าความชันของรอบก่อนหน้าซึ่งต้องใช้ในโมเมนตัมแบบเนสเตรอฟ
อนึ่ง ในส่วนบรรทัดสุดท้ายที่ปรับค่า w นั้นจำเป็นต้องใช้เป็น w += self.dw ไม่ใช่ w = w+ self.dw ดูเผินๆจะคิดว่าเหมือนกัน แต่หากใช้อย่างหลัง w จะกลายเป็นสร้างอาเรย์ใหม่ขึ้นแต่อาเรย์เดิมจะไม่มีการปรับค่า ตรงนี้เป็นเกร็ดเล็กน้อย เป็นเรื่องปลีกย่อยสำหรับพฤติกรรมของ ndarray
ลองดูตัวอย่างการใช้ พอนิยามคลาสแล้วเราจะเขียนใหม่ได้ดังนี้เพื่อให้ได้ผลเหมือนกับวิธีที่ทำตอนแรก
w = np.array([-7,2.])
opt = Nag(eta=0.004)
#opt = Mmtsgd(eta=0.004)
#opt = Sgd(eta=0.04)
w_ = [w.copy()]
for i in range(100):
gw = dJ(w)
opt(w,gw)
w_.append(w.copy())
w_ = np.stack(w_)
plot(w_)ในที่นี้ opt ถูกสร้างมาเป็นออบเจ็กต์ในคลาส Nag จากนั้นพอเข้าสู่วังวน for โดยที่ทุกรอบจะมีการเรียกใช้ opt ซึ่งจะทำสิ่งที่อยู่ในเมธอด __call__ ที่นิยามไว้ ผลก็คือตัวแปร w เปลี่ยนค่าไปเรื่อยๆทุกครั้ง เข้าใกล้จุดต่ำสุดไปเรื่อยๆ
ดูเผินๆอาจมองว่าทำเป็นคลาสแล้วยุ่งยากกว่าเดิม แต่ว่าแบบนี้เหมาะกับการนำมาใช้งานจริง
ต่อมาสำหรับคลาสของออปทิไมเซอร์ตระกูล Ada ทั้งหลายนิยามดังนี้
class Adagrad:
def __init__(self,eta=0.01):
self.eta = eta
self.G = 1e-7
def __call__(self,w,gw):
self.G += gw**2
w += -self.eta*gw/np.sqrt(self.G)
class Adadelta:
def __init__(self,eta=0.01,rho=0.95):
self.eta = eta
self.rho = rho
self.G = 1e-7
def __call__(self,w,gw):
self.G = self.rho*self.G+(1-self.rho)*gw**2
w += -self.eta*gw/np.sqrt(self.G)
class Adam:
def __init__(self,eta=0.001,beta1=0.9,beta2=0.999):
self.eta = eta
self.beta1 = beta1
self.beta2 = beta2
self.i = 1
self.m = 0
self.v = 1e-7
def __call__(self,w,gw):
self.m = self.beta1*self.m+(1-self.beta1)*gw
self.v = self.beta2*self.v+(1-self.beta2)*gw**2
w += -self.eta*np.sqrt(1-self.beta2**self.i)/(1-self.beta1**self.i)*self.m/np.sqrt(self.v)
self.i += 1จากนั้นตรงนี้จะเป็นตัวอย่างในการสร้างคลาสถดถอยโลจิสติกที่สามารถตั้งให้ใช้ออปทิไมเซอร์เหล่านี้ตามที่ต้องการได้
คลาสที่จะเขียนต่อไปนี้มีพื้นฐานจากคลาส ThotthoiLogistic ในหน้า https://phyblas.hinaboshi.com/20161228
แต่เอามาปรับปรุงโดยเปลี่ยนส่วนนิยามคลาสจากที่เดิมตอนสร้างใส่ค่าอัตราการเรียนรู้ (eta) เป็นมาใส่ออปทิไมเซอร์ (opt) แทน
def sigmoid(x):
return 1/(1+np.exp(-x))
class ThotthoiLogistic:
def __init__(self,opt):
self.opt = opt # เก็บ optimizer แทนที่จะเก็บอัตราการเรียนรู้ (η)
def rianru(self,X,z,n_thamsam,n_batch=0):
n = len(z)
if(n_batch==0 or n<n_batch):
n_batch = n
X_std = X.std()
X_std[X_std==0] = 1
X_mean = X.mean()
X = (X-X_mean)/X_std
self.w = np.zeros(X.shape[1]+1)
gw = self.w*0
self.entropy = []
self.thuktong = []
for j in range(n_thamsam):
lueak = np.random.permutation(n)
for i in range(0,n,n_batch):
Xn = X[lueak[i:i+n_batch]]
zn = z[lueak[i:i+n_batch]]
phi = self.ha_sigmoid(Xn)
eee = (phi-zn)/len(zn)
gw[1:] = np.dot(eee,Xn)
gw[0] = eee.sum()
self.opt(self.w,gw) # ใช้ optimizer เพื่อปรับค่าน้ำหนัก
thukmai = self.thamnai(X)==z
self.thuktong += [thukmai.mean()*100]
self.entropy += [self.ha_entropy(X,z)]
self.w[1:] /= X_std
self.w[0] -= (self.w[1:]*X_mean).sum()
def thamnai(self,X):
return np.dot(X,self.w[1:])+self.w[0]>0
def ha_sigmoid(self,X):
return sigmoid(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z):
phi = self.ha_sigmoid(X)
return -(z*np.log(phi+1e-7)+(1-z)*np.log(1-phi+1e-7)).mean()จากนั้นลองดูตัวอย่างการใช้งาน โดยลองสร้างข้อมูลเป็นกลุ่มก้อน จากนั้นใช้ AdaGrad ในการเรียนรู้ (รายละเอียดของ datasets.make_blobs https://phyblas.hinaboshi.com/20161127)
from sklearn import datasets
np.random.seed(4)
X,z = datasets.make_blobs(n_samples=12000,n_features=2,centers=2,cluster_std=2,random_state=2)
tl = ThotthoiLogistic(Adagrad(eta=1)) # ใส่ออบเจ็กต์ของออปทิไมเซอร์ไปแทนที่จะใส่แค่ eta โดยตรง
tl.rianru(X,z,n_thamsam=50,n_batch=150)
plt.figure(figsize=[6,8])
x_sen = np.array([X[:,0].min(),X[:,0].max()])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
tm = tl.thamnai(X)==z
plt.axes(aspect=1,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.plot(x_sen,y_sen,'y',lw=3,zorder=0)
plt.scatter(X[tm,0],X[tm,1],c=z[tm],alpha=0.5,s=20,edgecolor='k',lw=0.5,cmap='winter')
plt.scatter(X[~tm,0],X[~tm,1],c=z[~tm],alpha=0.5,s=20,edgecolor='r',cmap='winter')
plt.show()ผลที่ได้ก็สามารถแบ่งข้อมูลออกมาได้แบบนี้

สุดท้าย ลองมาสร้างกราฟแสดงความคืบหน้าในการเรียนรู้เปรียบเทียบวิธีต่างๆกันดู
plt.figure(figsize=[8,8])
ax1 = plt.subplot(211)
ax1.set_title(u'เอนโทรปี',fontname='Tahoma')
ax1.tick_params(labelbottom='off')
ax2 = plt.subplot(212)
ax2.set_title(u'% ถูก',fontname='Tahoma')
opt = [Sgd(0.2),
Mmtsgd(0.2),
Nag(0.2),
Adagrad(0.2),
Adadelta(0.2),
Adam(0.2)]
for o in opt:
tl = ThotthoiLogistic(o)
tl.rianru(X,z,n_thamsam=40,n_batch=150)
si = np.random.random(3)
ax1.plot(tl.entropy,color=si)
ax2.plot(tl.thuktong,color=si)
ax2.legend(['SGD','Momentum','NAG','AdaGrad','AdaDelta','Adam'],ncol=2)
plt.show()
อย่างไรก็ตาม กราฟนี้ได้แค่เปรียบเทียบว่าหากอัตราการเรียนรู้เท่ากันจะเป็นยังไงเท่านั้น ไม่อาจบอกได้ว่าวิธีไหนดีกว่า
เวลาไหนควรใช้วิธีไหนดีที่สุดนั้นยังเป็นเรื่องที่ต้องทำวิจัยกันต่อไป
อ้างอิง
แหล่งอ้างอิงหลัก
https://www.oreilly.co.jp/books/9784873117584
อื่นๆ
https://www.amazon.co.jp/dp/B072JC21DH
http://blog.csdn.net/luo123n/article/details/48239963
http://blog.csdn.net/u014595019/article/details/52989301
http://blog.csdn.net/alwaystry/article/details/60478501
http://ycszen.github.io/2016/08/24/SGD,Adagrad,Adadelta,Adam等优化方法总结和比较
http://cpmarkchang.logdown.com/posts/434534-optimization-method-momentum
http://cpmarkchang.logdown.com/posts/275500-optimization-method-adagrad
http://cpmarkchang.logdown.com/posts/467674-optimization-method-adadelta
https://zhuanlan.zhihu.com/p/21486826
https://zhuanlan.zhihu.com/p/22810533
https://morvanzhou.github.io/tutorials/machine-learning/ML-intro/3-06-speed-up-learning
https://www.oreilly.co.jp/books/9784873117584
อื่นๆ
https://www.amazon.co.jp/dp/B072JC21DH
http://blog.csdn.net/luo123n/article/details/48239963
http://blog.csdn.net/u014595019/article/details/52989301
http://blog.csdn.net/alwaystry/article/details/60478501
http://ycszen.github.io/2016/08/24/SGD,Adagrad,Adadelta,Adam等优化方法总结和比较
http://cpmarkchang.logdown.com/posts/434534-optimization-method-momentum
http://cpmarkchang.logdown.com/posts/275500-optimization-method-adagrad
http://cpmarkchang.logdown.com/posts/467674-optimization-method-adadelta
https://zhuanlan.zhihu.com/p/21486826
https://zhuanlan.zhihu.com/p/22810533
https://morvanzhou.github.io/tutorials/machine-learning/ML-intro/3-06-speed-up-learning
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib