[python] การทำมินิแบตช์ในการเรียนรู้ของเครื่อง
เขียนเมื่อ 2016/12/28 01:39
แก้ไขล่าสุด 2022/07/21 15:19
จากที่ก่อนหน้านี้ได้เขียนถึงการปรับปรุงแบบจำลองการถดถอยโลจิสติกและการถดถอยซอฟต์แม็กซ์ไป https://phyblas.hinaboshi.com/20161207
ต่อจากนั้นยังมีอีกส่วนที่สามารถปรับปรุงเพิ่มเติมต่อให้ดียิ่งขึ้นได้อีก นั่นก็คือการทำมินิแบตช์ (minibatch)
เดิมทีเวลาที่ให้โปรแกรมเรียนรู้จากข้อมูลเราจะใช้ข้อมูลทั้งหมดที่ใส่เข้าไปมาหาค่าเสียหาย (เอนโทรปี หรือความคลาดเคลื่อนกำลังสอง) พร้อมกันทีเดียวทั้งหมด
แต่การใช้ข้อมูลทั้งหมดพร้อมกันทีเดียวแบบนั้นมีข้อเสียอยู่ หนึ่งคือหากข้อมูลมีจำนวนมหาศาลจะใช้เวลาในการคำนวณนานมาก
และอีกอย่างก็คือทำแบบนี้มีโอกาสที่จะได้คำตอบเป็นค่าที่มีค่าความเสียหายเป็นค่ำต่ำสุดสัมพัทธ์ แทนที่จะเป็นค่าต่ำสุดสมบูรณ์
กล่าวคือคำตอบที่ได้นั้นอาจไม่ใช่คำตอบที่ดีที่สุด แต่เป็นคำตอบที่พอจะใช้ได้ที่โปรแกรมหาเจอก่อนแล้วพอใจที่จะหยุดอยู่แค่ตรงนั้นโดยไม่ค้นหาคำตอบที่อาจจะดีกว่านี้ต่อ
การแก้ปัญหานี้ ทำได้โดยการปรับปรุงโปรแกรมตรงส่วนที่ทำการเรียนรู้จากข้อมูล โดยแทนที่จะใช้ข้อมูลทั้งหมดทีเดียวก็ให้คำนวณค่าเสียหายจากข้อมูลแค่บางส่วนที่สุ่มขึ้นมาจากข้อมูลทั้งหมด แล้วเรียนรู้จากตรงนั้นแล้วปรับค่าน้ำหนักและไบแอสไปทีหนึ่ง จากนั้นก็สุ่มข้อมูลชุดต่อไปแล้วทำการเรียนรู้ใหม่ จนใช้ข้อมูลทั้งหมดที่มี จึงจะนับเป็นการเรียนรู้หนึ่งรอบ
นั่นคือในการเรียนรู้หนึ่งรอบแทนที่จะเอาข้อมูลทั้งหมดมาเรียนรู้เพื่อปรับค่าน้ำหนักและไบแอสครั้งเดียว ก็ให้ค่อยๆเรียนรู้ปรับค่าไปทีละนิดด้วยข้อมูลคนละชุดที่สุ่มมา
ข้อมูลแต่ละชุดจะมีค่าเสียหายที่คำนวณได้ไม่เท่ากัน ดังนั้นในการคำนวณแต่ละครั้งโอกาสที่ค่าน้ำหนักจะลู่เข้าสู่ค่าที่ได้ค่าเสียหายเป็นแค่ค่าต่ำสุดสัมพัทธ์ก็จะลดลง
กรณีที่ทำมินิแบตช์ ค่าเสียหายที่จะคำนวณควรจะใช้เป็นค่าเฉลี่ย แทนที่จะใช้ค่าผลรวม
กล่าวคือ หากค่าเสียหายเป็นเอนโทรปี ก็ต้องเอาเอนโทรปีมาหารจำนวนข้อมูลที่ใช้ในแต่ละครั้งเป็นเอนโทรปีเฉลี่ย
หากใช้เป็นความคลาดเคลื่อนกำลังสองก็ต้องเอาผลรวมความคลาดเคลื่อนกำลังสอง (和方差, SSE) มาหารจำนวนข้อมูล กลายเป็นค่าเฉลี่ยความคลาดเคลื่อนกำลังสอง (均方差, MSE, mean squared errror)
MSE = SSE ÷ จำนวนข้อมูล
หากใช้ค่าเป็นผลรวมโดยไม่หารจำนวนก็จะทำให้ยิ่งข้อมูลมีจำนวนมากก็ยิ่งเรียนรู้เร็วแม้ว่าค่าอัตราการเรียนรู้จะเท่ากัน แต่ถ้าใช้ค่าเฉลี่ยไม่ว่าจะมีข้อมูลมากแค่ไหนก็เรียนรู้ในอัตราที่เท่ากัน
ในที่นี้จะลองเขียนโค้ดใหม่โดยแก้จากแบบจำลองการถดถอยโลจิสติกและซอฟต์แม็กซ์ที่ใช้เอนโทรปีใน https://phyblas.hinaboshi.com/20161207
โดยจะแก้ให้ใช้ค่าเอนโทรปีเฉลี่ยเป็นค่าเสียดายแทนเอนโทรปีรวม และแก้ให้สามารถทำมินิแบตช์ได้
ในการสุ่มให้ข้อมูลออกมาตามลำดับในแต่ละรอบนั้นสามารถใช้ฟังก์ชัน np.random.permutation รายละเอียดของฟังก์ชันนี้อ่านได้ใน >> numpy เบื้องต้นบทที่ ๑๕
เริ่มจากลองทำกับแบบจำลองการถดถอยโลจิสติกสำหรับแบ่งกลุ่มสองกลุ่ม
การทำมินิแบตช์นั้นจะทำให้โค้ดดูซับซ้อนขึ้นไปอีก โดยจะต้องมีการเพิ่มวังวน for เข้ามาอีกชั้น
for ด้านนอกเป็นการวนซ้ำเพื่อการเรียนรู้ในแต่ละรอบตามจำนวนครั้ง n_thamsam
ส่วน for ด้านในเป็นการวนซ้ำเพื่อทำมินิแบตช์ให้ใช้ข้อมูลทีละชุดที่สุ่มมาเป็นจำนวนเท่ากับ n_batch จากข้อมูลทั้งหมด n ตัว พอวนทำซ้ำจนจบข้อมูลทั้งหมดจะถูกใช้ทั้งหมด
len(zn) คือจำนวนข้อมูลที่ถูกใช้ในแต่ละรอบ ซึ่งจะเท่ากับ n_batch ยกเว้นตลอดยกเว้นรอบสุดท้ายจะเป็นจำนวนเศษที่เหลืออยู่
อีกส่วนที่มีการเปลี่ยนแปลงคือเมธอด ha_entropy แทนที่จะใช้ sum ต่อท้ายก็เปลี่ยนเป็น mean แทน
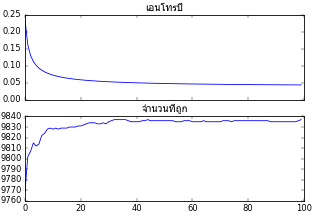
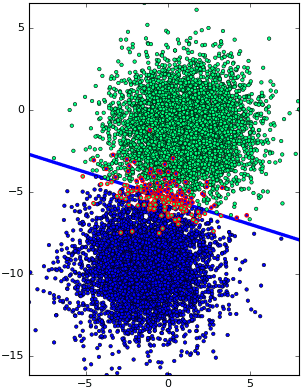
ได้คลาสของแบบจำลองการถดถอยโลจิสติกมาแล้ว จากนั้นลองนำคลาสมาใช้ดู โดยตัวอย่างคราวนี้ขอยก datasets.make_blobs มาใช้ สร้างข้อมูลตัวอย่างมา 10000 แต่ใช้จำนวนแบตช์แค่ 150
ผลที่ได้ก็ทำได้ดีเช่นเดียวกับตอนที่ไม่ใช้มินิแบตช์
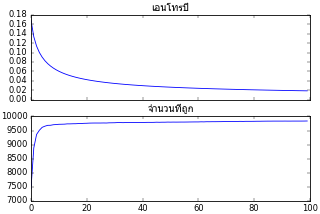
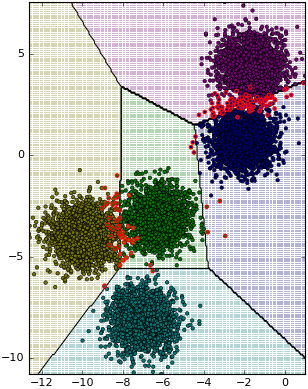
จากนั้นลองทำแบบเดียวกันกับแบบจำลองการถดถอยโลจิสติกแบบมัลติโนเมียล (การถดถอยซอฟต์แม็กซ์) ซึ่งใช้แบ่งข้อมูลเป็นหลายกลุ่ม
ตัวอย่างก็ลองใช้ datasets.make_blobs เช่นกัน
อ้างอิง
ต่อจากนั้นยังมีอีกส่วนที่สามารถปรับปรุงเพิ่มเติมต่อให้ดียิ่งขึ้นได้อีก นั่นก็คือการทำมินิแบตช์ (minibatch)
เดิมทีเวลาที่ให้โปรแกรมเรียนรู้จากข้อมูลเราจะใช้ข้อมูลทั้งหมดที่ใส่เข้าไปมาหาค่าเสียหาย (เอนโทรปี หรือความคลาดเคลื่อนกำลังสอง) พร้อมกันทีเดียวทั้งหมด
แต่การใช้ข้อมูลทั้งหมดพร้อมกันทีเดียวแบบนั้นมีข้อเสียอยู่ หนึ่งคือหากข้อมูลมีจำนวนมหาศาลจะใช้เวลาในการคำนวณนานมาก
และอีกอย่างก็คือทำแบบนี้มีโอกาสที่จะได้คำตอบเป็นค่าที่มีค่าความเสียหายเป็นค่ำต่ำสุดสัมพัทธ์ แทนที่จะเป็นค่าต่ำสุดสมบูรณ์
กล่าวคือคำตอบที่ได้นั้นอาจไม่ใช่คำตอบที่ดีที่สุด แต่เป็นคำตอบที่พอจะใช้ได้ที่โปรแกรมหาเจอก่อนแล้วพอใจที่จะหยุดอยู่แค่ตรงนั้นโดยไม่ค้นหาคำตอบที่อาจจะดีกว่านี้ต่อ
การแก้ปัญหานี้ ทำได้โดยการปรับปรุงโปรแกรมตรงส่วนที่ทำการเรียนรู้จากข้อมูล โดยแทนที่จะใช้ข้อมูลทั้งหมดทีเดียวก็ให้คำนวณค่าเสียหายจากข้อมูลแค่บางส่วนที่สุ่มขึ้นมาจากข้อมูลทั้งหมด แล้วเรียนรู้จากตรงนั้นแล้วปรับค่าน้ำหนักและไบแอสไปทีหนึ่ง จากนั้นก็สุ่มข้อมูลชุดต่อไปแล้วทำการเรียนรู้ใหม่ จนใช้ข้อมูลทั้งหมดที่มี จึงจะนับเป็นการเรียนรู้หนึ่งรอบ
นั่นคือในการเรียนรู้หนึ่งรอบแทนที่จะเอาข้อมูลทั้งหมดมาเรียนรู้เพื่อปรับค่าน้ำหนักและไบแอสครั้งเดียว ก็ให้ค่อยๆเรียนรู้ปรับค่าไปทีละนิดด้วยข้อมูลคนละชุดที่สุ่มมา
ข้อมูลแต่ละชุดจะมีค่าเสียหายที่คำนวณได้ไม่เท่ากัน ดังนั้นในการคำนวณแต่ละครั้งโอกาสที่ค่าน้ำหนักจะลู่เข้าสู่ค่าที่ได้ค่าเสียหายเป็นแค่ค่าต่ำสุดสัมพัทธ์ก็จะลดลง
กรณีที่ทำมินิแบตช์ ค่าเสียหายที่จะคำนวณควรจะใช้เป็นค่าเฉลี่ย แทนที่จะใช้ค่าผลรวม
กล่าวคือ หากค่าเสียหายเป็นเอนโทรปี ก็ต้องเอาเอนโทรปีมาหารจำนวนข้อมูลที่ใช้ในแต่ละครั้งเป็นเอนโทรปีเฉลี่ย
หากใช้เป็นความคลาดเคลื่อนกำลังสองก็ต้องเอาผลรวมความคลาดเคลื่อนกำลังสอง (和方差, SSE) มาหารจำนวนข้อมูล กลายเป็นค่าเฉลี่ยความคลาดเคลื่อนกำลังสอง (均方差, MSE, mean squared errror)
MSE = SSE ÷ จำนวนข้อมูล
หากใช้ค่าเป็นผลรวมโดยไม่หารจำนวนก็จะทำให้ยิ่งข้อมูลมีจำนวนมากก็ยิ่งเรียนรู้เร็วแม้ว่าค่าอัตราการเรียนรู้จะเท่ากัน แต่ถ้าใช้ค่าเฉลี่ยไม่ว่าจะมีข้อมูลมากแค่ไหนก็เรียนรู้ในอัตราที่เท่ากัน
ในที่นี้จะลองเขียนโค้ดใหม่โดยแก้จากแบบจำลองการถดถอยโลจิสติกและซอฟต์แม็กซ์ที่ใช้เอนโทรปีใน https://phyblas.hinaboshi.com/20161207
โดยจะแก้ให้ใช้ค่าเอนโทรปีเฉลี่ยเป็นค่าเสียดายแทนเอนโทรปีรวม และแก้ให้สามารถทำมินิแบตช์ได้
ในการสุ่มให้ข้อมูลออกมาตามลำดับในแต่ละรอบนั้นสามารถใช้ฟังก์ชัน np.random.permutation รายละเอียดของฟังก์ชันนี้อ่านได้ใน >> numpy เบื้องต้นบทที่ ๑๕
เริ่มจากลองทำกับแบบจำลองการถดถอยโลจิสติกสำหรับแบ่งกลุ่มสองกลุ่ม
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
class ThotthoiLogistic:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam,n_batch=0):
n = len(z) # จำนวนข้อมูลทั้งหมด
# ถ้าไม่ได้กำหนดจำนวนแบตช์ หรือจำนวนแบตช์มากกว่าจำนวนข้อมูล
if(n_batch==0 or n<n_batch):
n_batch = n # ให้ทำด้วยจำนวนทั้งหมด (คือไม่ทำมินิแบตช์)
X_std = X.std()
X_std[X_std==0] = 1
X_mean = X.mean()
X = (X-X_mean)/X_std # ทำให้เป็นมาตรฐาน
self.w = np.zeros(X.shape[1]+1)
self.entropy = []
self.thuktong = []
for j in range(n_thamsam):
# สุ่มเลขลำดับการเลือก
lueak = np.random.permutation(n)
for i in range(0,n,n_batch):
# เลือก X และ z บางส่วนตามลำดับ
Xn = X[lueak[i:i+n_batch]]
zn = z[lueak[i:i+n_batch]]
# ปรับค่าน้ำหนัก
phi = self.ha_sigmoid(Xn)
eee = (zn-phi)/len(zn)*self.eta
self.w[1:] += np.dot(eee,Xn)
self.w[0] += eee.sum()
# คำนวณและบันทึกผลในแต่ละรอบ
thukmai = self.thamnai(X)==z
self.thuktong += [thukmai.sum()]
self.entropy += [self.ha_entropy(X,z)]
self.w[1:] /= X_std
self.w[0] -= (self.w[1:]*X_mean).sum()
def thamnai(self,X):
return np.dot(X,self.w[1:])+self.w[0]>0
def ha_sigmoid(self,X):
return sigmoid(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z):
phi = self.ha_sigmoid(X)
return -(z*np.log(phi+1e-7)+(1-z)*np.log(1-phi+1e-7)).mean()
def sigmoid(x):
return 1/(1+np.exp(-x))
class ThotthoiLogistic:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam,n_batch=0):
n = len(z) # จำนวนข้อมูลทั้งหมด
# ถ้าไม่ได้กำหนดจำนวนแบตช์ หรือจำนวนแบตช์มากกว่าจำนวนข้อมูล
if(n_batch==0 or n<n_batch):
n_batch = n # ให้ทำด้วยจำนวนทั้งหมด (คือไม่ทำมินิแบตช์)
X_std = X.std()
X_std[X_std==0] = 1
X_mean = X.mean()
X = (X-X_mean)/X_std # ทำให้เป็นมาตรฐาน
self.w = np.zeros(X.shape[1]+1)
self.entropy = []
self.thuktong = []
for j in range(n_thamsam):
# สุ่มเลขลำดับการเลือก
lueak = np.random.permutation(n)
for i in range(0,n,n_batch):
# เลือก X และ z บางส่วนตามลำดับ
Xn = X[lueak[i:i+n_batch]]
zn = z[lueak[i:i+n_batch]]
# ปรับค่าน้ำหนัก
phi = self.ha_sigmoid(Xn)
eee = (zn-phi)/len(zn)*self.eta
self.w[1:] += np.dot(eee,Xn)
self.w[0] += eee.sum()
# คำนวณและบันทึกผลในแต่ละรอบ
thukmai = self.thamnai(X)==z
self.thuktong += [thukmai.sum()]
self.entropy += [self.ha_entropy(X,z)]
self.w[1:] /= X_std
self.w[0] -= (self.w[1:]*X_mean).sum()
def thamnai(self,X):
return np.dot(X,self.w[1:])+self.w[0]>0
def ha_sigmoid(self,X):
return sigmoid(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z):
phi = self.ha_sigmoid(X)
return -(z*np.log(phi+1e-7)+(1-z)*np.log(1-phi+1e-7)).mean()
การทำมินิแบตช์นั้นจะทำให้โค้ดดูซับซ้อนขึ้นไปอีก โดยจะต้องมีการเพิ่มวังวน for เข้ามาอีกชั้น
for ด้านนอกเป็นการวนซ้ำเพื่อการเรียนรู้ในแต่ละรอบตามจำนวนครั้ง n_thamsam
ส่วน for ด้านในเป็นการวนซ้ำเพื่อทำมินิแบตช์ให้ใช้ข้อมูลทีละชุดที่สุ่มมาเป็นจำนวนเท่ากับ n_batch จากข้อมูลทั้งหมด n ตัว พอวนทำซ้ำจนจบข้อมูลทั้งหมดจะถูกใช้ทั้งหมด
len(zn) คือจำนวนข้อมูลที่ถูกใช้ในแต่ละรอบ ซึ่งจะเท่ากับ n_batch ยกเว้นตลอดยกเว้นรอบสุดท้ายจะเป็นจำนวนเศษที่เหลืออยู่
อีกส่วนที่มีการเปลี่ยนแปลงคือเมธอด ha_entropy แทนที่จะใช้ sum ต่อท้ายก็เปลี่ยนเป็น mean แทน
ได้คลาสของแบบจำลองการถดถอยโลจิสติกมาแล้ว จากนั้นลองนำคลาสมาใช้ดู โดยตัวอย่างคราวนี้ขอยก datasets.make_blobs มาใช้ สร้างข้อมูลตัวอย่างมา 10000 แต่ใช้จำนวนแบตช์แค่ 150
import matplotlib.pyplot as plt
from sklearn import datasets
X,z = datasets.make_blobs(n_samples=10000,n_features=2,centers=2,cluster_std=2,random_state=2)
eta = 0.1
n_thamsam = 100
n_batch = 150
tl = ThotthoiLogistic(eta)
tl.rianru(X,z,n_thamsam,n_batch)
plt.subplot(211)
plt.title(u'เอนโทรปี',fontname='Tahoma')
plt.plot(tl.entropy)
plt.tick_params(labelbottom='off')
plt.subplot(212)
plt.title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.figure(figsize=[6,6])
x_sen = np.array([X[:,0].min(),X[:,0].max()])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(X)==z
plt.axes(aspect=1,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.plot(x_sen,y_sen,lw=3,zorder=0)
plt.scatter(X[thukmai,0],X[thukmai,1],c=z[thukmai],s=10,edgecolor='k',lw=0.5,cmap='winter')
plt.scatter(X[~thukmai,0],X[~thukmai,1],c=z[~thukmai],s=10,edgecolor='r',cmap='winter')
plt.show()
from sklearn import datasets
X,z = datasets.make_blobs(n_samples=10000,n_features=2,centers=2,cluster_std=2,random_state=2)
eta = 0.1
n_thamsam = 100
n_batch = 150
tl = ThotthoiLogistic(eta)
tl.rianru(X,z,n_thamsam,n_batch)
plt.subplot(211)
plt.title(u'เอนโทรปี',fontname='Tahoma')
plt.plot(tl.entropy)
plt.tick_params(labelbottom='off')
plt.subplot(212)
plt.title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.figure(figsize=[6,6])
x_sen = np.array([X[:,0].min(),X[:,0].max()])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(X)==z
plt.axes(aspect=1,xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()])
plt.plot(x_sen,y_sen,lw=3,zorder=0)
plt.scatter(X[thukmai,0],X[thukmai,1],c=z[thukmai],s=10,edgecolor='k',lw=0.5,cmap='winter')
plt.scatter(X[~thukmai,0],X[~thukmai,1],c=z[~thukmai],s=10,edgecolor='r',cmap='winter')
plt.show()
ผลที่ได้ก็ทำได้ดีเช่นเดียวกับตอนที่ไม่ใช้มินิแบตช์


จากนั้นลองทำแบบเดียวกันกับแบบจำลองการถดถอยโลจิสติกแบบมัลติโนเมียล (การถดถอยซอฟต์แม็กซ์) ซึ่งใช้แบ่งข้อมูลเป็นหลายกลุ่ม
import numpy as np
def softmax(x):
exp_x = np.exp(x.T-x.max(1))
return (exp_x/exp_x.sum(0)).T
class ThotthoiSoftmax:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam,n_batch=0):
n = len(z)
if(n_batch==0 or n<n_batch):
n_batch = n
self.kiklum = int(z.max()+1)
X_std = X.std(0)
X_std[X_std==0] = 1
X_mean = X.mean(0)
X = (X-X_mean)/X_std
z_1h = z[:,None]==range(self.kiklum)
self.w = np.zeros([X.shape[1]+1,self.kiklum])
self.entropy = []
self.thuktong = []
for j in range(n_thamsam):
lueak = np.random.permutation(n)
for i in range(0,n,n_batch):
Xn = X[lueak[i:i+n_batch]]
zn = z_1h[lueak[i:i+n_batch]]
phi = self.ha_softmax(Xn)
eee = (zn-phi)/len(zn)*self.eta
self.w[1:] += np.dot(eee.T,Xn).T
self.w[0] += eee.sum(0)
thukmai = self.thamnai(X)==z
self.thuktong += [thukmai.sum()]
self.entropy += [self.ha_entropy(X,z_1h)]
self.w[1:] /= X_std[:,None]
self.w[0] -= (self.w[1:]*X_mean[:,None]).sum(0)
def thamnai(self,X):
return (np.dot(X,self.w[1:])+self.w[0]).argmax(1)
def ha_softmax(self,X):
return softmax(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z_1h):
return -(z_1h*np.log(self.ha_softmax(X)+1e-7)).mean()
def softmax(x):
exp_x = np.exp(x.T-x.max(1))
return (exp_x/exp_x.sum(0)).T
class ThotthoiSoftmax:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam,n_batch=0):
n = len(z)
if(n_batch==0 or n<n_batch):
n_batch = n
self.kiklum = int(z.max()+1)
X_std = X.std(0)
X_std[X_std==0] = 1
X_mean = X.mean(0)
X = (X-X_mean)/X_std
z_1h = z[:,None]==range(self.kiklum)
self.w = np.zeros([X.shape[1]+1,self.kiklum])
self.entropy = []
self.thuktong = []
for j in range(n_thamsam):
lueak = np.random.permutation(n)
for i in range(0,n,n_batch):
Xn = X[lueak[i:i+n_batch]]
zn = z_1h[lueak[i:i+n_batch]]
phi = self.ha_softmax(Xn)
eee = (zn-phi)/len(zn)*self.eta
self.w[1:] += np.dot(eee.T,Xn).T
self.w[0] += eee.sum(0)
thukmai = self.thamnai(X)==z
self.thuktong += [thukmai.sum()]
self.entropy += [self.ha_entropy(X,z_1h)]
self.w[1:] /= X_std[:,None]
self.w[0] -= (self.w[1:]*X_mean[:,None]).sum(0)
def thamnai(self,X):
return (np.dot(X,self.w[1:])+self.w[0]).argmax(1)
def ha_softmax(self,X):
return softmax(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z_1h):
return -(z_1h*np.log(self.ha_softmax(X)+1e-7)).mean()
ตัวอย่างก็ลองใช้ datasets.make_blobs เช่นกัน
X,z = datasets.make_blobs(n_samples=10000,n_features=2,centers=5,cluster_std=0.8,random_state=1)
eta = 0.1
n_thamsam = 100
n_batch = 150
ts = ThotthoiSoftmax(eta)
ts.rianru(X,z,n_thamsam,n_batch)
ax = plt.subplot(211)
ax.set_title(u'เอนโทรปี',fontname='Tahoma')
plt.plot(ts.entropy)
plt.tick_params(labelbottom='off')
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(ts.thuktong)
plt.figure(figsize=[6,6])
ax = plt.axes(xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()],aspect=1)
nmesh = 200
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),nmesh),np.linspace(X[:,1].min(),X[:,1].max(),nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = ts.thamnai(mX)
si = ['#770077','#777700','#007777','#007700','#000077']
c = [si[i] for i in mz]
ax.scatter(mX[:,0],mX[:,1],c=c,s=1,marker='s',alpha=0.3,lw=0)
ax.contour(mx,my,mz.reshape(nmesh,nmesh),
ts.kiklum,colors='k',lw=2,zorder=0)
thukmai = ts.thamnai(X)==z
c = np.array([si[i] for i in z])
ax.scatter(X[thukmai,0],X[thukmai,1],c=c[thukmai],s=10,edgecolor='k',lw=0.5)
ax.scatter(X[~thukmai,0],X[~thukmai,1],c=c[~thukmai],s=10,edgecolor='r')
plt.show()
eta = 0.1
n_thamsam = 100
n_batch = 150
ts = ThotthoiSoftmax(eta)
ts.rianru(X,z,n_thamsam,n_batch)
ax = plt.subplot(211)
ax.set_title(u'เอนโทรปี',fontname='Tahoma')
plt.plot(ts.entropy)
plt.tick_params(labelbottom='off')
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(ts.thuktong)
plt.figure(figsize=[6,6])
ax = plt.axes(xlim=[X[:,0].min(),X[:,0].max()],ylim=[X[:,1].min(),X[:,1].max()],aspect=1)
nmesh = 200
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),nmesh),np.linspace(X[:,1].min(),X[:,1].max(),nmesh))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = ts.thamnai(mX)
si = ['#770077','#777700','#007777','#007700','#000077']
c = [si[i] for i in mz]
ax.scatter(mX[:,0],mX[:,1],c=c,s=1,marker='s',alpha=0.3,lw=0)
ax.contour(mx,my,mz.reshape(nmesh,nmesh),
ts.kiklum,colors='k',lw=2,zorder=0)
thukmai = ts.thamnai(X)==z
c = np.array([si[i] for i in z])
ax.scatter(X[thukmai,0],X[thukmai,1],c=c[thukmai],s=10,edgecolor='k',lw=0.5)
ax.scatter(X[~thukmai,0],X[~thukmai,1],c=c[~thukmai],s=10,edgecolor='r')
plt.show()


อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib