[python] เอนโทรปีไขว้ในการวิเคราะห์การถดถอยโลจิสติก
เขียนเมื่อ 2016/12/07 23:23
แก้ไขล่าสุด 2022/07/21 15:29
จากบทความแรกที่เขียนถึงการวิเคราะห์การถดถอยโลจิสติกเบื้องต้น https://phyblas.hinaboshi.com/20161103
และล่าสุดที่เขียนถึงการวิเคราะห์การถดถอยโลจิสติกแบบมัลติโนเมียล (การถดถอยซอฟต์แม็กซ์) https://phyblas.hinaboshi.com/20161205
ในโค้ดที่เขียนไปทั้งหมดในนั้นใช้ฟังก์ชันค่าเสียหายเป็นผลรวมความคลาดเคลื่อนกำลังสอง (和方差, sum of squared error, SSE) มาตลอด
อย่างไรก็ตามความจริงแล้วในการวิเคราะห์การถดถอยโลจิสติกนั้นจะไม่ใช้ผลรวมความคลาดเคลื่อนกำลังสอง แต่ใช้ค่าที่เรียกว่าเอนโทรปีไขว้ (交叉熵, cross entropy)
ที่เลือกใช้ผลรวมความคลาดเคลื่อนกำลังสองแทนที่จะใช้เอนโทรปีตั้งแต่ต้นก็เพราะเข้าใจง่ายกว่า แต่เพื่อให้แบบจำลองเป็นไปในแบบที่ควรจะเป็นมากขึ้น ในบทความนี้จะทำการเขียนคลาสขึ้นใหม่โดยแก้ตรงส่วนของฟังก์ชันค่าเสียหายให้ใช้เอนโทรปีแทน
เอนโทรปี (熵, entropy) หมายถึงความไม่เป็นระเบียบ เป็นปริมาณที่มักถูกใช้ในทางอุณหพลศาสตร์ https://th.wikipedia.org/wiki/เอนโทรปี
เอนโทรปีไขว้คือเอนโทรปีที่ถูกใช้ในทฤษฎีสารสนเทศ https://th.wikipedia.org/wiki/เอนโทรปีของข้อมูล
หลักการใกล้เคียงกัน คือบอกถึงความไม่เป็นระเบียบของข้อมูล คือบอกว่าการจัดกลุ่มของข้อมูลเป็นไปอย่างที่ควรจะเป็นแค่ไหน
ความไม่เป็นระเบียบจะมากขึ้นเมื่อค่าของข้อมูลไม่เป็นไปอย่างที่ควรจะเป็น คือยิ่งมีมากยิ่งไม่ดี ดังนั้นการลดความไม่เป็นระเบียบคือการทำให้ข้อมูลถูกต้องยิ่งขึ้น
ดังนั้นจึงใช้เป็นฟังก์ชันค่าเสียหายสำหรับการเรียนรู้ของเครื่อง ในลักษณะเดียวกับผลรวมความคลาดเคลื่อนกำลังสอง
เอนโทรปีไขว้สำหรับการวิเคราะห์ถดถอยโลจิสติกสำหรับจัดข้อมูลเป็น ๒ กลุ่มสามารถคำนวณได้ดังนี้
..(1)
ที่มาของมันมาจากการพิจารณาค่าลอการิธึมของความควรจะเป็น (log-likelihood) ในที่นี้จะไม่พูดถึงรายละเอียด
ในที่นี้ z คือคำตอบจริง (เป็น 1 หรือ 0) ส่วน φ คือผลที่คำนวณมาจากฟังก์ชันซิกมอยด์ (ค่าอยู่ระหว่าง 0 ถึง 1)
..(2)
โดย a คือผลรวมของผลคูณระหว่างตัวแปรต้นกับน้ำหนัก
..(3)
โดย xj คือตัวแปรต้นตัวที่ j และ wj คือค่าน้ำหนักของตัวแปรต้นตัวที่ j โดยในที่นี้ยังรวมไปถึงพจน์ของไบแอส (w0) ด้วย โดยไบแอสจะไม่ได้คูณกับอะไร เป็น w0 โดดๆตัวเดียว
การหาความชันเทียบกับค่าน้ำหนักทำได้โดยหาอนุพันธ์ย่อย สามารถใช้กฎลูกโซ่ดังนี้
..(4)
จากสมการ (1) หาอนุพันธ์ของ J เทียบกับ φ ได้
..(5)
จากสมการ (2) หาอนุพันธ์ของ φ เทียบกับ a ได้
..(6)
และจากสมการ (3) หาอนุพันธ์ของ a เทียบกับ wj ได้
..(7)
นำ (5) (6) (7) ทั้งหมดแทนลงใน (4) ได้
..(8)
สมการดูเหมือนยุ่งยากกว่าตอนใช้ผลรวมความคลาดเคลื่อนกำลังสอง แต่พอแก้หาค่าอนุพันธ์ออกมาแล้วกลับดูเรียบง่ายกว่ามาก
จากนั้นนำความชันที่ได้มาหาที่ควรจะปรับตามสูตร
..(9)
โดย η คืออัตราการเรียนรู้
นำ (8) แทนลงใน (9) ได้
..(10)
นำสมการนี้มาใช้ในการเขียนโค้ดสร้างคลาสแบบจำลองถดถอยโลจิสติกใหม่โดยแก้จากคลาส ThotthoiLogistic โค้ดที่ได้ใส่กระบวนการปรับมาตรฐานแล้วที่ได้เขียนไว้ใน https://phyblas.hinaboshi.com/20161124
เขียนได้ดังนี้
ในโค้ดนี้มีจุดที่ต้องอธิบายเสริมอีกนิดก็คือในส่วนของเมธอด ha_entropy มีการเพิ่ม +1e-7 ลงไป ใน log ด้วย ที่เพิ่มไปก็เพื่อป้องกันกรณีที่ค่า phi เป็น 0 ซึ่งจะทำให้ค่า log ออกมาเป็นลบอนันต์
อีกอย่างหนึ่งคือ ฟังก์ชัน np.log ใน numpy นี้ไม่ใช่การหาลอการิธึมฐาน 10 แต่เป็นฐานธรรมชาติ ดังนั้นจึงเทียบเท่ากับ ln ในสมการ
ลองนำมาใช้ดูโดยสร้างโจทย์ง่ายๆขึ้นมาเช่นเดิม คราวนี้ลองทั้งโจทย์เป็นการปลูกมันฝรั่งแล้วขุดรากมาดูว่าผลที่ได้ใหญ่หรือเปล่าแล้วสรุปผลว่าดินตรงไหนอุดมสมบูรณ์หรือไม่
ผลการปลูกเป็นดังนี้
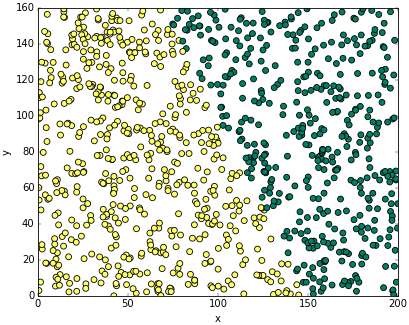
สีเหลืองคือได้ผลเล็ก สีเขียวคือได้ผลใหญ่
โค้ดสำหรับสร้างข้อมูลตามนี้ก็คือ
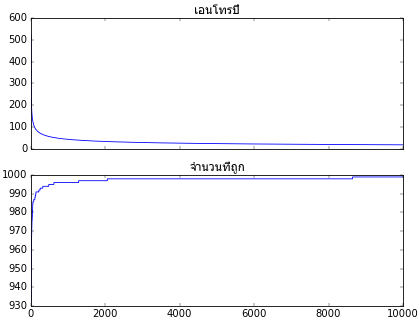
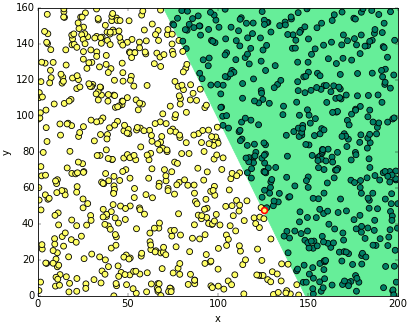
ต่อไปก็เริ่มนำคลาสที่สร้างขึ้นมาใช้ แล้ววาดกราฟความคืบหน้าในการเรียนรู้ แล้วก็แสดงผลการจำแนกที่ได้
ต่อมาลองมาดูกรณีของการจำแนกข้อมูลหลายกลุ่ม หรือที่เรียกว่าการวิเคราะห์การถดถอยซอฟต์แม็กซ์ หลักการก็คล้ายกัน
สำหรับกรณีนี้เอนโทรปีไขว้จะคำนวณได้ดังนี้
..(11)
โดย zm ในที่นี้เป็นค่าคำตอบจริงในรูป one-hot
โดย k คือดัชนีของกลุ่มประเภทที่ต้องการแบ่ง ซึ่งจะเห็นได้ว่าหากมีแค่ ๒ กลุ่ม สมการที่ได้จะมีลักษณะเหมือนกับสมการ (1)
และ φk ในที่นี้คือผลการคำนวณจากฟังก์ชันซอฟต์แม็กซ์ในแต่ละกลุ่ม k
..(12)
am คือผลรวมของผลคูณระหว่างตัวแปรต้น xj กับน้ำหนัก wjm
..(13)
หาความชันของเอนโทรปีไขว้เทียบกับน้ำหนักได้โดย
..(14)
จากสมการ (11) หาอนุพันธ์ของ J เทียบกับ φk ได้
..(15)
จากสมการ (12) หาอนุพันธ์ของ φm เทียบกับ am ได้
..(16)
และจากสมการ (13) หาอนุพันธ์ของ am เทียบกับ wjm ได้
..(17)
นำ (15) (16) (17) ทั้งหมดแทนลงใน (14) ได้
..(18)
จัดรูปใหม่ได้เป็น
..(19)
แต่ zk คือค่าผลลัพธ์ในรูป one-hot จะมี 1 อยู่กลุ่มเดียวนอกนั้นเป็น 0 ดังนั้นหากรวมทุกกลุ่มจะต้องเป็น 1 เสมอ ดังนั้น
..(20)
ดังนั้น
..(21)
จะเห็นว่าสมการดูเรียบง่ายลงมากเมื่อเทียบกับตอนที่ใช้ผลรวมความคลาดเคลื่อนกำลังสอง
จากนั้นก็คำนวณความเปลี่ยนแปลงน้ำหนักในแต่ละรอบการเรียนรู้ได้โดย
..(22)
แทน (21) ลงใน (22) ได้เป็น
..(23)
นำสมการมาใช้เขียนโค้ดสร้างคลาสของแบบจำลองวิเคราะห์การถดถอยซอฟต์แม็กซ์ใหม่โดยแก้จากฟังก์ชัน ThotthoiSoftmax ใน https://phyblas.hinaboshi.com/20161205
ได้เป็น
จะเห็นว่าโค้ดสั้นเรียบง่ายขึ้นกว่าพอสมควร
ลองสร้างโจทย์ขึ้นมาเพื่อทดสอบการใช้คลาสที่สร้างมานี้ดู คราวนี้เปลี่ยนจากเลี้ยงพญานาคมาเป็นเลี้ยงมังกรบ้าง
สมมุติว่ามีเกมเกมหนึ่งซึ่งในเกมมีการเลี้ยงมังกรและพอเลี้ยงถึงจุดหนึ่งมังกรจะเปลี่ยนร่าง โดยร่างที่จะเปลี่ยนนั้นจะต่างกันไปขึ้นกับอาหารที่ให้ โดยสมมุติว่าอาหารมังกรมีอยู่แค่ ๒ แบบคือ เนื้อสัตว์กับผลไม้ ผู้เล่นคนหนึ่งลองเลี้ยงมังกร ๒๐๐ ตัวโดยให้อาหารต่างๆกันแล้วดูว่าเปลี่ยนร่างเป็นแบบไหน ผลการเลี้ยงเป็นไปตามนี้
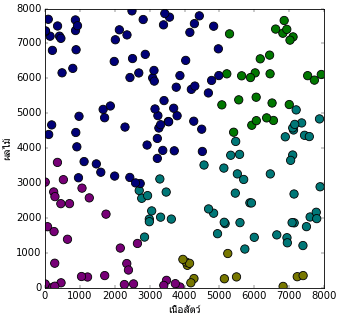
โดย
0. สีม่วง มังกรตาย
1. สีเหลือง มังกรเหลือง
2. สีฟ้า มังกรฟ้า
3. สีเขียว มังกรเขียว
4. สีน้ำเงิน มังกรน้ำเงิน
โค้ดที่ใช้สร้างก็คือ
ลองนำมาเริ่มการเรียนรู้โดยดูผลความคืบหน้าในการเรียนรู้พร้อมวาดผลการจำแนกกลุ่มประเภท
เท่านี้ก็จะเห็นได้ว่าสามารถใช้เอนโทรปีเป็นค่าเสียหายแทนผลรวมความคลาดเคลื่อนกำลังสอง
ต่อจากนี้ไปสำหรับแบบจำลองการวิเคราะห์การถดถอยโลจิสติกและซอฟต์แม็กซ์ก็จะใช้เอนโทรปีเป็นหลัก เพราะทั้งเขียนง่ายกว่า และใช้กันทั่วไปมากกว่า
อ้างอิง
และล่าสุดที่เขียนถึงการวิเคราะห์การถดถอยโลจิสติกแบบมัลติโนเมียล (การถดถอยซอฟต์แม็กซ์) https://phyblas.hinaboshi.com/20161205
ในโค้ดที่เขียนไปทั้งหมดในนั้นใช้ฟังก์ชันค่าเสียหายเป็นผลรวมความคลาดเคลื่อนกำลังสอง (和方差, sum of squared error, SSE) มาตลอด
อย่างไรก็ตามความจริงแล้วในการวิเคราะห์การถดถอยโลจิสติกนั้นจะไม่ใช้ผลรวมความคลาดเคลื่อนกำลังสอง แต่ใช้ค่าที่เรียกว่าเอนโทรปีไขว้ (交叉熵, cross entropy)
ที่เลือกใช้ผลรวมความคลาดเคลื่อนกำลังสองแทนที่จะใช้เอนโทรปีตั้งแต่ต้นก็เพราะเข้าใจง่ายกว่า แต่เพื่อให้แบบจำลองเป็นไปในแบบที่ควรจะเป็นมากขึ้น ในบทความนี้จะทำการเขียนคลาสขึ้นใหม่โดยแก้ตรงส่วนของฟังก์ชันค่าเสียหายให้ใช้เอนโทรปีแทน
เอนโทรปี (熵, entropy) หมายถึงความไม่เป็นระเบียบ เป็นปริมาณที่มักถูกใช้ในทางอุณหพลศาสตร์ https://th.wikipedia.org/wiki/เอนโทรปี
เอนโทรปีไขว้คือเอนโทรปีที่ถูกใช้ในทฤษฎีสารสนเทศ https://th.wikipedia.org/wiki/เอนโทรปีของข้อมูล
หลักการใกล้เคียงกัน คือบอกถึงความไม่เป็นระเบียบของข้อมูล คือบอกว่าการจัดกลุ่มของข้อมูลเป็นไปอย่างที่ควรจะเป็นแค่ไหน
ความไม่เป็นระเบียบจะมากขึ้นเมื่อค่าของข้อมูลไม่เป็นไปอย่างที่ควรจะเป็น คือยิ่งมีมากยิ่งไม่ดี ดังนั้นการลดความไม่เป็นระเบียบคือการทำให้ข้อมูลถูกต้องยิ่งขึ้น
ดังนั้นจึงใช้เป็นฟังก์ชันค่าเสียหายสำหรับการเรียนรู้ของเครื่อง ในลักษณะเดียวกับผลรวมความคลาดเคลื่อนกำลังสอง
เอนโทรปีไขว้สำหรับการวิเคราะห์ถดถอยโลจิสติกสำหรับจัดข้อมูลเป็น ๒ กลุ่มสามารถคำนวณได้ดังนี้
..(1)
ที่มาของมันมาจากการพิจารณาค่าลอการิธึมของความควรจะเป็น (log-likelihood) ในที่นี้จะไม่พูดถึงรายละเอียด
ในที่นี้ z คือคำตอบจริง (เป็น 1 หรือ 0) ส่วน φ คือผลที่คำนวณมาจากฟังก์ชันซิกมอยด์ (ค่าอยู่ระหว่าง 0 ถึง 1)
..(2)
โดย a คือผลรวมของผลคูณระหว่างตัวแปรต้นกับน้ำหนัก
..(3)
โดย xj คือตัวแปรต้นตัวที่ j และ wj คือค่าน้ำหนักของตัวแปรต้นตัวที่ j โดยในที่นี้ยังรวมไปถึงพจน์ของไบแอส (w0) ด้วย โดยไบแอสจะไม่ได้คูณกับอะไร เป็น w0 โดดๆตัวเดียว
การหาความชันเทียบกับค่าน้ำหนักทำได้โดยหาอนุพันธ์ย่อย สามารถใช้กฎลูกโซ่ดังนี้
..(4)
จากสมการ (1) หาอนุพันธ์ของ J เทียบกับ φ ได้
..(5)
จากสมการ (2) หาอนุพันธ์ของ φ เทียบกับ a ได้
..(6)
และจากสมการ (3) หาอนุพันธ์ของ a เทียบกับ wj ได้
..(7)
นำ (5) (6) (7) ทั้งหมดแทนลงใน (4) ได้
..(8)
สมการดูเหมือนยุ่งยากกว่าตอนใช้ผลรวมความคลาดเคลื่อนกำลังสอง แต่พอแก้หาค่าอนุพันธ์ออกมาแล้วกลับดูเรียบง่ายกว่ามาก
จากนั้นนำความชันที่ได้มาหาที่ควรจะปรับตามสูตร
..(9)
โดย η คืออัตราการเรียนรู้
นำ (8) แทนลงใน (9) ได้
..(10)
นำสมการนี้มาใช้ในการเขียนโค้ดสร้างคลาสแบบจำลองถดถอยโลจิสติกใหม่โดยแก้จากคลาส ThotthoiLogistic โค้ดที่ได้ใส่กระบวนการปรับมาตรฐานแล้วที่ได้เขียนไว้ใน https://phyblas.hinaboshi.com/20161124
เขียนได้ดังนี้
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
class ThotthoiLogistic:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam):
X_std = X.std()
X_std[X_std==0] = 1
X_mean = X.mean()
self.entropy = []
self.thuktong = []
self.w = np.zeros(X.shape[1]+1)
X = (X-X_mean)/X_std
phi = self.ha_sigmoid(X)
for i in range(n_thamsam):
eee = (z-phi)*self.eta
self.w[1:] += np.dot(X.T,eee)
self.w[0] += eee.sum()
phi = self.ha_sigmoid(X)
thukmai = np.abs(phi-z)<0.5
self.thuktong += [thukmai.sum()]
self.entropy += [self.ha_entropy(X,z)]
self.w[1:] /= X_std
self.w[0] -= (self.w[1:]*X_mean).sum()
def thamnai(self,X):
return np.dot(X,self.w[1:])+self.w[0]>0
def ha_sigmoid(self,X):
return sigmoid(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z):
phi = self.ha_sigmoid(X)
return -(z*np.log(phi+1e-7)+(1-z)*np.log(1-phi+1e-7)).sum()
def sigmoid(x):
return 1/(1+np.exp(-x))
class ThotthoiLogistic:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam):
X_std = X.std()
X_std[X_std==0] = 1
X_mean = X.mean()
self.entropy = []
self.thuktong = []
self.w = np.zeros(X.shape[1]+1)
X = (X-X_mean)/X_std
phi = self.ha_sigmoid(X)
for i in range(n_thamsam):
eee = (z-phi)*self.eta
self.w[1:] += np.dot(X.T,eee)
self.w[0] += eee.sum()
phi = self.ha_sigmoid(X)
thukmai = np.abs(phi-z)<0.5
self.thuktong += [thukmai.sum()]
self.entropy += [self.ha_entropy(X,z)]
self.w[1:] /= X_std
self.w[0] -= (self.w[1:]*X_mean).sum()
def thamnai(self,X):
return np.dot(X,self.w[1:])+self.w[0]>0
def ha_sigmoid(self,X):
return sigmoid(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z):
phi = self.ha_sigmoid(X)
return -(z*np.log(phi+1e-7)+(1-z)*np.log(1-phi+1e-7)).sum()
ในโค้ดนี้มีจุดที่ต้องอธิบายเสริมอีกนิดก็คือในส่วนของเมธอด ha_entropy มีการเพิ่ม +1e-7 ลงไป ใน log ด้วย ที่เพิ่มไปก็เพื่อป้องกันกรณีที่ค่า phi เป็น 0 ซึ่งจะทำให้ค่า log ออกมาเป็นลบอนันต์
อีกอย่างหนึ่งคือ ฟังก์ชัน np.log ใน numpy นี้ไม่ใช่การหาลอการิธึมฐาน 10 แต่เป็นฐานธรรมชาติ ดังนั้นจึงเทียบเท่ากับ ln ในสมการ
ลองนำมาใช้ดูโดยสร้างโจทย์ง่ายๆขึ้นมาเช่นเดิม คราวนี้ลองทั้งโจทย์เป็นการปลูกมันฝรั่งแล้วขุดรากมาดูว่าผลที่ได้ใหญ่หรือเปล่าแล้วสรุปผลว่าดินตรงไหนอุดมสมบูรณ์หรือไม่
ผลการปลูกเป็นดังนี้

สีเหลืองคือได้ผลเล็ก สีเขียวคือได้ผลใหญ่
โค้ดสำหรับสร้างข้อมูลตามนี้ก็คือ
import matplotlib.pyplot as plt
x_manfarang = np.random.uniform(0,200,1000)
y_manfarang = np.random.uniform(0,160,1000)
yaimai = (2*x_manfarang+y_manfarang-300>0).astype(int)
plt.axes(aspect=1,xlim=[0,200],ylim=[0,160],xlabel='x',ylabel='y')
plt.scatter(x_manfarang,y_manfarang,c=yaimai,s=50,edgecolor='k',cmap='summer_r')
plt.show()
x_manfarang = np.random.uniform(0,200,1000)
y_manfarang = np.random.uniform(0,160,1000)
yaimai = (2*x_manfarang+y_manfarang-300>0).astype(int)
plt.axes(aspect=1,xlim=[0,200],ylim=[0,160],xlabel='x',ylabel='y')
plt.scatter(x_manfarang,y_manfarang,c=yaimai,s=50,edgecolor='k',cmap='summer_r')
plt.show()
ต่อไปก็เริ่มนำคลาสที่สร้างขึ้นมาใช้ แล้ววาดกราฟความคืบหน้าในการเรียนรู้ แล้วก็แสดงผลการจำแนกที่ได้
eta = 0.001
n_thamsam = 10000
xy_manfarang = np.stack([x_manfarang,y_manfarang],axis=1)
tl = ThotthoiLogistic(eta)
tl.rianru(xy_manfarang,yaimai,n_thamsam)
ax = plt.subplot(211)
ax.set_title(u'เอนโทรปี',fontname='Tahoma')
plt.plot(tl.entropy)
plt.tick_params(labelbottom='off')
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
x_sen = np.array([0,200])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(xy_manfarang)==yaimai
plt.show()
plt.figure(figsize=[8,6])
plt.axes(aspect=1,xlim=[0,200],ylim=[0,160],xlabel='x',ylabel='y')
if(tl.w[1]*tl.w[2]<0):
plt.fill_between(x_sen,y_sen,[0,0],color='#66ee99')
else:
plt.fill_between(x_sen,y_sen,[200,160],color='#66ee99')
plt.scatter(x_manfarang[thukmai],y_manfarang[thukmai],c=yaimai[thukmai],s=50,edgecolor='k',cmap='summer_r')
plt.scatter(x_manfarang[~thukmai],y_manfarang[~thukmai],c=yaimai[~thukmai],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()
n_thamsam = 10000
xy_manfarang = np.stack([x_manfarang,y_manfarang],axis=1)
tl = ThotthoiLogistic(eta)
tl.rianru(xy_manfarang,yaimai,n_thamsam)
ax = plt.subplot(211)
ax.set_title(u'เอนโทรปี',fontname='Tahoma')
plt.plot(tl.entropy)
plt.tick_params(labelbottom='off')
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
x_sen = np.array([0,200])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(xy_manfarang)==yaimai
plt.show()
plt.figure(figsize=[8,6])
plt.axes(aspect=1,xlim=[0,200],ylim=[0,160],xlabel='x',ylabel='y')
if(tl.w[1]*tl.w[2]<0):
plt.fill_between(x_sen,y_sen,[0,0],color='#66ee99')
else:
plt.fill_between(x_sen,y_sen,[200,160],color='#66ee99')
plt.scatter(x_manfarang[thukmai],y_manfarang[thukmai],c=yaimai[thukmai],s=50,edgecolor='k',cmap='summer_r')
plt.scatter(x_manfarang[~thukmai],y_manfarang[~thukmai],c=yaimai[~thukmai],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()


ต่อมาลองมาดูกรณีของการจำแนกข้อมูลหลายกลุ่ม หรือที่เรียกว่าการวิเคราะห์การถดถอยซอฟต์แม็กซ์ หลักการก็คล้ายกัน
สำหรับกรณีนี้เอนโทรปีไขว้จะคำนวณได้ดังนี้
..(11)
โดย zm ในที่นี้เป็นค่าคำตอบจริงในรูป one-hot
โดย k คือดัชนีของกลุ่มประเภทที่ต้องการแบ่ง ซึ่งจะเห็นได้ว่าหากมีแค่ ๒ กลุ่ม สมการที่ได้จะมีลักษณะเหมือนกับสมการ (1)
และ φk ในที่นี้คือผลการคำนวณจากฟังก์ชันซอฟต์แม็กซ์ในแต่ละกลุ่ม k
..(12)
am คือผลรวมของผลคูณระหว่างตัวแปรต้น xj กับน้ำหนัก wjm
..(13)
หาความชันของเอนโทรปีไขว้เทียบกับน้ำหนักได้โดย
..(14)
จากสมการ (11) หาอนุพันธ์ของ J เทียบกับ φk ได้
..(15)
จากสมการ (12) หาอนุพันธ์ของ φm เทียบกับ am ได้
..(16)
และจากสมการ (13) หาอนุพันธ์ของ am เทียบกับ wjm ได้
..(17)
นำ (15) (16) (17) ทั้งหมดแทนลงใน (14) ได้
..(18)
จัดรูปใหม่ได้เป็น
..(19)
แต่ zk คือค่าผลลัพธ์ในรูป one-hot จะมี 1 อยู่กลุ่มเดียวนอกนั้นเป็น 0 ดังนั้นหากรวมทุกกลุ่มจะต้องเป็น 1 เสมอ ดังนั้น
..(20)
ดังนั้น
..(21)
จะเห็นว่าสมการดูเรียบง่ายลงมากเมื่อเทียบกับตอนที่ใช้ผลรวมความคลาดเคลื่อนกำลังสอง
จากนั้นก็คำนวณความเปลี่ยนแปลงน้ำหนักในแต่ละรอบการเรียนรู้ได้โดย
..(22)
แทน (21) ลงใน (22) ได้เป็น
..(23)
นำสมการมาใช้เขียนโค้ดสร้างคลาสของแบบจำลองวิเคราะห์การถดถอยซอฟต์แม็กซ์ใหม่โดยแก้จากฟังก์ชัน ThotthoiSoftmax ใน https://phyblas.hinaboshi.com/20161205
ได้เป็น
import numpy as np
def softmax(x):
exp_x = np.exp(x.T-x.max(1))
return (exp_x/exp_x.sum(0)).T
class ThotthoiSoftmax:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam):
self.kiklum = int(z.max()+1)
X_std = X.std(0)
X_std[X_std==0] = 1
X_mean = X.mean(0)
X = (X-X_mean)/X_std
z_1h = z[:,None]==range(self.kiklum)
self.w = np.zeros([X.shape[1]+1,self.kiklum])
self.entropy = []
self.thuktong = []
phi = self.ha_softmax(X)
for i in range(n_thamsam):
eee = (z_1h-phi)*self.eta
self.w[1:] += np.dot(eee.T,X).T
self.w[0] += eee.sum(0)
phi = self.ha_softmax(X)
thukmai = phi.argmax(1)==z
self.thuktong += [thukmai.sum()]
self.entropy += [self.ha_entropy(X,z_1h)]
self.w[1:] /= X_std[:,None]
self.w[0] -= (self.w[1:]*X_mean[:,None]).sum(0)
def thamnai(self,X):
return (np.dot(X,self.w[1:])+self.w[0]).argmax(1)
def ha_softmax(self,X):
return softmax(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z_1h):
return -(z_1h*np.log(self.ha_softmax(X)+1e-7)).sum()
def softmax(x):
exp_x = np.exp(x.T-x.max(1))
return (exp_x/exp_x.sum(0)).T
class ThotthoiSoftmax:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam):
self.kiklum = int(z.max()+1)
X_std = X.std(0)
X_std[X_std==0] = 1
X_mean = X.mean(0)
X = (X-X_mean)/X_std
z_1h = z[:,None]==range(self.kiklum)
self.w = np.zeros([X.shape[1]+1,self.kiklum])
self.entropy = []
self.thuktong = []
phi = self.ha_softmax(X)
for i in range(n_thamsam):
eee = (z_1h-phi)*self.eta
self.w[1:] += np.dot(eee.T,X).T
self.w[0] += eee.sum(0)
phi = self.ha_softmax(X)
thukmai = phi.argmax(1)==z
self.thuktong += [thukmai.sum()]
self.entropy += [self.ha_entropy(X,z_1h)]
self.w[1:] /= X_std[:,None]
self.w[0] -= (self.w[1:]*X_mean[:,None]).sum(0)
def thamnai(self,X):
return (np.dot(X,self.w[1:])+self.w[0]).argmax(1)
def ha_softmax(self,X):
return softmax(np.dot(X,self.w[1:])+self.w[0])
def ha_entropy(self,X,z_1h):
return -(z_1h*np.log(self.ha_softmax(X)+1e-7)).sum()
จะเห็นว่าโค้ดสั้นเรียบง่ายขึ้นกว่าพอสมควร
ลองสร้างโจทย์ขึ้นมาเพื่อทดสอบการใช้คลาสที่สร้างมานี้ดู คราวนี้เปลี่ยนจากเลี้ยงพญานาคมาเป็นเลี้ยงมังกรบ้าง
สมมุติว่ามีเกมเกมหนึ่งซึ่งในเกมมีการเลี้ยงมังกรและพอเลี้ยงถึงจุดหนึ่งมังกรจะเปลี่ยนร่าง โดยร่างที่จะเปลี่ยนนั้นจะต่างกันไปขึ้นกับอาหารที่ให้ โดยสมมุติว่าอาหารมังกรมีอยู่แค่ ๒ แบบคือ เนื้อสัตว์กับผลไม้ ผู้เล่นคนหนึ่งลองเลี้ยงมังกร ๒๐๐ ตัวโดยให้อาหารต่างๆกันแล้วดูว่าเปลี่ยนร่างเป็นแบบไหน ผลการเลี้ยงเป็นไปตามนี้

โดย
0. สีม่วง มังกรตาย
1. สีเหลือง มังกรเหลือง
2. สีฟ้า มังกรฟ้า
3. สีเขียว มังกรเขียว
4. สีน้ำเงิน มังกรน้ำเงิน
โค้ดที่ใช้สร้างก็คือ
nueasat = np.random.randint(0,8000,200)
phonlamai = np.random.randint(0,8000,200)
plianrang = np.tile([4],200)
plianrang[nueasat>5000] = 3
plianrang[nueasat-phonlamai*2>-3000] = 2
plianrang[phonlamai<1000] = 1
plianrang[nueasat+phonlamai<4000] = 0
si = ['#770077','#777700','#007777','#007700','#000077']
c = [si[i] for i in plianrang]
plt.figure(figsize=[6,6])
ax = plt.axes(xlim=[0,8000],ylim=[0,8000],aspect=1)
ax.set_xlabel(u'เนื้อสัตว์',fontname='Tahoma')
ax.set_ylabel(u'ผลไม้',fontname='Tahoma')
ax.scatter(nueasat,phonlamai,c=c,s=100)
plt.show()
phonlamai = np.random.randint(0,8000,200)
plianrang = np.tile([4],200)
plianrang[nueasat>5000] = 3
plianrang[nueasat-phonlamai*2>-3000] = 2
plianrang[phonlamai<1000] = 1
plianrang[nueasat+phonlamai<4000] = 0
si = ['#770077','#777700','#007777','#007700','#000077']
c = [si[i] for i in plianrang]
plt.figure(figsize=[6,6])
ax = plt.axes(xlim=[0,8000],ylim=[0,8000],aspect=1)
ax.set_xlabel(u'เนื้อสัตว์',fontname='Tahoma')
ax.set_ylabel(u'ผลไม้',fontname='Tahoma')
ax.scatter(nueasat,phonlamai,c=c,s=100)
plt.show()
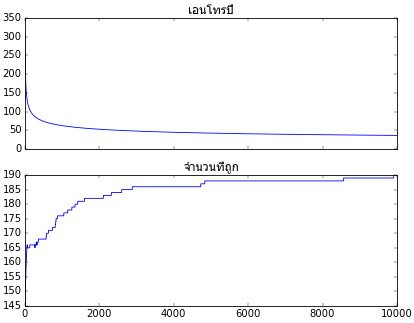
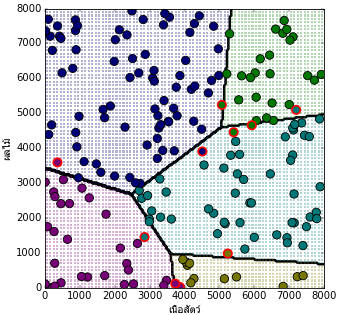
ลองนำมาเริ่มการเรียนรู้โดยดูผลความคืบหน้าในการเรียนรู้พร้อมวาดผลการจำแนกกลุ่มประเภท
eta = 0.001
n_thamsam = 10000
ahan = np.stack([nueasat,phonlamai],axis=1)
ts = ThotthoiSoftmax(eta)
ts.rianru(ahan,plianrang,n_thamsam)
ax = plt.subplot(211)
ax.set_title(u'เอนโทรปี',fontname='Tahoma')
plt.plot(ts.entropy)
plt.tick_params(labelbottom='off')
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(ts.thuktong)
plt.figure(figsize=[6,6])
ax = plt.axes(xlim=[0,8000],ylim=[0,8000],aspect=1)
ax.set_xlabel(u'เนื้อสัตว์',fontname='Tahoma')
ax.set_ylabel(u'ผลไม้',fontname='Tahoma')
nmesh = 200
mx,my = np.meshgrid(np.linspace(0,8000,nmesh),np.linspace(0,8000,nmesh))
mx = mx.ravel()
my = my.ravel()
mX = np.stack([mx,my],1)
mz = ts.thamnai(mX)
c = [si[i] for i in mz]
ax.scatter(mx,my,c=c,s=1,marker='s',alpha=0.3,lw=0)
ax.contour(mx.reshape(nmesh,nmesh),my.reshape(nmesh,nmesh),mz.reshape(nmesh,nmesh),
ts.kiklum,colors='k',linewidths=3,zorder=0)
thukmai = ts.thamnai(ahan)==plianrang
c = np.array([si[i] for i in plianrang])
ax.scatter(nueasat[thukmai],phonlamai[thukmai],c=c[thukmai],s=100,edgecolor='k')
ax.scatter(nueasat[~thukmai],phonlamai[~thukmai],c=c[~thukmai],s=100,edgecolor='r',lw=2)
plt.show()
n_thamsam = 10000
ahan = np.stack([nueasat,phonlamai],axis=1)
ts = ThotthoiSoftmax(eta)
ts.rianru(ahan,plianrang,n_thamsam)
ax = plt.subplot(211)
ax.set_title(u'เอนโทรปี',fontname='Tahoma')
plt.plot(ts.entropy)
plt.tick_params(labelbottom='off')
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(ts.thuktong)
plt.figure(figsize=[6,6])
ax = plt.axes(xlim=[0,8000],ylim=[0,8000],aspect=1)
ax.set_xlabel(u'เนื้อสัตว์',fontname='Tahoma')
ax.set_ylabel(u'ผลไม้',fontname='Tahoma')
nmesh = 200
mx,my = np.meshgrid(np.linspace(0,8000,nmesh),np.linspace(0,8000,nmesh))
mx = mx.ravel()
my = my.ravel()
mX = np.stack([mx,my],1)
mz = ts.thamnai(mX)
c = [si[i] for i in mz]
ax.scatter(mx,my,c=c,s=1,marker='s',alpha=0.3,lw=0)
ax.contour(mx.reshape(nmesh,nmesh),my.reshape(nmesh,nmesh),mz.reshape(nmesh,nmesh),
ts.kiklum,colors='k',linewidths=3,zorder=0)
thukmai = ts.thamnai(ahan)==plianrang
c = np.array([si[i] for i in plianrang])
ax.scatter(nueasat[thukmai],phonlamai[thukmai],c=c[thukmai],s=100,edgecolor='k')
ax.scatter(nueasat[~thukmai],phonlamai[~thukmai],c=c[~thukmai],s=100,edgecolor='r',lw=2)
plt.show()


เท่านี้ก็จะเห็นได้ว่าสามารถใช้เอนโทรปีเป็นค่าเสียหายแทนผลรวมความคลาดเคลื่อนกำลังสอง
ต่อจากนี้ไปสำหรับแบบจำลองการวิเคราะห์การถดถอยโลจิสติกและซอฟต์แม็กซ์ก็จะใช้เอนโทรปีเป็นหลัก เพราะทั้งเขียนง่ายกว่า และใช้กันทั่วไปมากกว่า
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib