[python] การวิเคราะห์องค์ประกอบหลักของข้อมูลที่ใช้ในการเรียนรู้ของเครื่อง
เขียนเมื่อ 2018/07/27 10:29
แก้ไขล่าสุด 2024/10/12 09:29
เมื่อวิเคราะห์ปัญหาต่างๆโดยอาศัยการเรียนรู้ของเครื่องนั้น การเลือกตัวแปรต่างๆที่จะนำมาพิจารณาให้เหมาะสมนั้นเป็นเรื่องสำคัญ
การพิจารณาตัวแปรที่ไม่จำเป็นเยอะเกินจำเป็นอาจทำให้เกิดปัญหาการเรียนรู้เกิน (过学习, overlearning)
ก่อนหน้านี้ได้แนะนำเรื่องการลดตัวแปรของปัญหาในการเรียนรู้ของเครื่องด้วยวิธีการคัดเลือกค่าแทนลักษณะ (特征选择, feature selection) https://phyblas.hinaboshi.com/20171211
อย่างไรก็ตาม นั่นเป็นเพียงแค่การคัดเลือกตัวแปรจากเดิมทีที่มีอยู่แล้วว่าตัวไหนจำเป็นและตัดบางตัวทิ้งเท่านั้น
แต่มีอีกแนวทางหนึ่งที่อาจจะได้ผลดีกว่า ก็คือสร้างชุดตัวแปรใหม่ขึ้นจากชุดตัวแปรเดิมที่มีอยู่
วิธีการหนึ่งที่เป็นที่นิยมก็คือ การวิเคราะห์องค์ประกอบหลัก (主成分分析, principle component Analysis) หรือนิยมเรียกย่อว่า PCA
แนวคิด
การวิเคราะห์องค์ประกอบหลักคือการเอาข้อมูลซึ่งอยู่ในระบบพิกัดของชุดตัวแปรเดิมมาแปลงให้อยู่ในรูปของชุดตัวแปรใหม่ โดยเมื่อแปลงเสร็จแล้วตัวแปรใหม่จะมีทั้งที่สำคัญและไม่สำคัญก็ตัดตัวที่ไม่สำคัญทิ้งไป
ยกตัวอย่างเช่นมีข้อมูลสามมิติที่มีการแจกแจงตามนี้
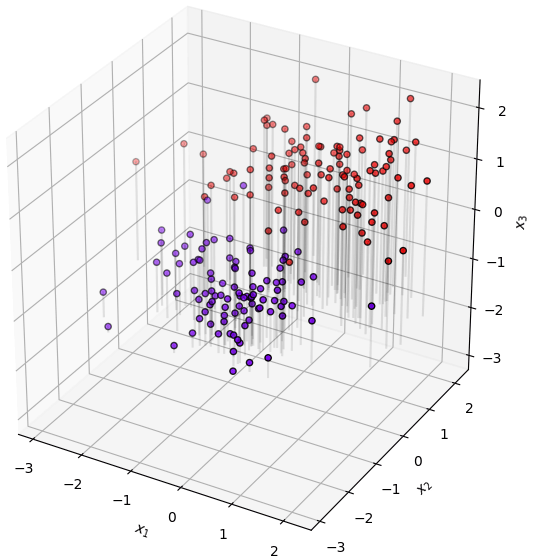
พอพลิกแกนดูในแนวนึงจะเห็นว่ามันวางตัวเกือบจะเป็นแผ่นจานแบน
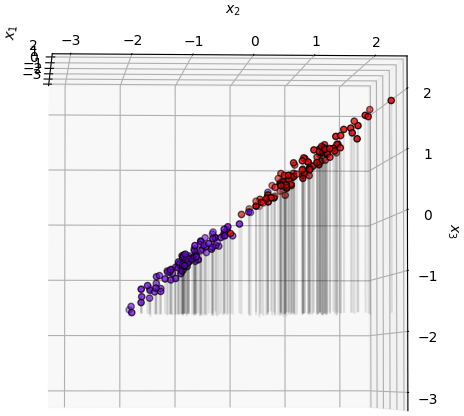
แบบนั้นแล้วหากเราแค่พิจารณาค่าแค่ตามแนวระนาบสองมิติก็น่าจะพอ
การที่จะพิจารณาข้อมูลตามแนวนั้นได้สะดวกก็คือ ทำการย้ายพิกัด สร้างแกนใหม่ให้วางแนวตามนี้
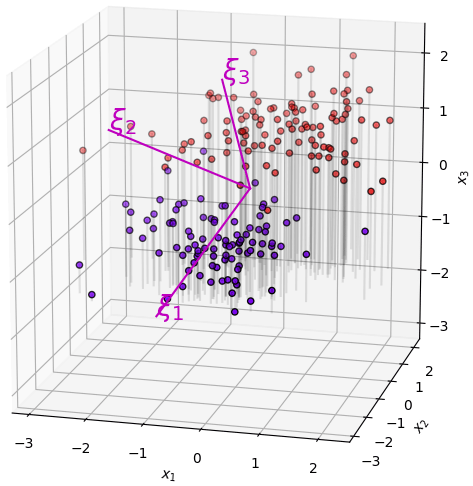
แล้วพอหมุนเปลี่ยนระบบพิกัดมาเป็นตามแกนนั้นก็จะกลายเป็นแบบนี้
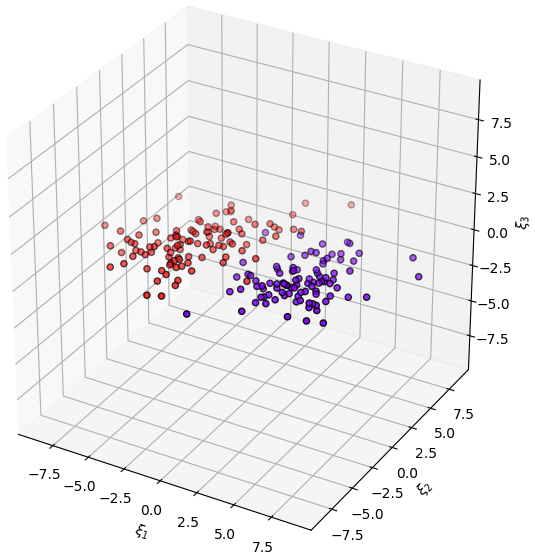
เท่านี้ก็จะสามารถละแกนตั้งทิ้งไปได้เลย แล้วเขียนเป็นสองมิติได้แบบนี้
นี่คือแนวคิดของการวิเคราะห์องค์ประกอบหลัก คือตั้งระบบพิกัดใหม่ หาแกนที่มีการกระจายตัวสูง แล้วตัดเอาแกนที่มีการกระจายตัวต่ำทิ้ง ช่วยลดจำนวนมิติของข้อมูลได้
วิธีการ
ในการแปลงระบบพิกัดนั้นวิธีพื้นฐานที่ง่ายที่สุดคือการแปลงเชิงเส้น คือเขียนระบบพิกัดใหม่โดยคำนวณจาก
..(1)
โดยในที่นี้ใช้ ξ1,ξ2,... แทนระบบพิกัดใหม่ ส่วน x1,x2,... แทนระบบพิกัดเดิม มีจำนวน m มิติ แต่ละตัวมีคุณสมบัติตั้งฉาก (正交, orthogonal)
v คือค่าน้ำหนักในการแปลง
เขียนค่าพิกัดใหม่แต่ละตัวในรูปเวกเตอร์ได้แบบนี้
..(2)
เอาองค์ประกอบทั้งหมดมาเขียนในรูปเมทริกซ์ก็จะได้แบบนี้
..(3)
โดย
..(4)
..(5)
โดย V เป็นเมทริกซ์เชิงตั้งฉาก (正交矩阵, orthogonal matrix) รวบรวมค่าน้ำหนักทั้งหมดในการแปลง
..(6)
ในบทความนี้จะใช้สัญลักษณ์ลูกศรบนหัวแทนเวกเตอร์ (= เมทริกซ์มิติเดียว) ส่วนอักษรตัวหนาแทนเมทริกซ์สองมิติ ถ้าอักษรตัวเอียงธรรมดาจะแทนเลขเดี่ยว
ดังนั้นระบบพิกัดใหม่เขียนสั้นๆได้เป็น
..(7)
หรือเขียนใหม่แสดงเป็นเมทริกซ์ในแนวตั้งก็เป็น (จากสมบัติของเมทริกซ์)
..(8)
ทีนี้เป้าหมายก็คือหาว่าเมทริกซ์ V ควรจะหน้าตาเป็นยังไง
เป้าหมายของเราคือการหาแกนใหม่ตามขนาดการกระจายตัวของข้อมูล ดังนั้นสิ่งที่ควรจะพิจารณาก็คือ ความแปรปรวนร่วมเกี่ยว (协方差, covariance) ของข้อมูล
เกี่ยวเรื่องความแปรปรวนร่วมเกี่ยวได้เขียนถึงไว้แล้วใน https://phyblas.hinaboshi.com/20180517
เมทริกซ์ความแปรปรวนร่วมเกี่ยวแสดงได้โดย
..(9)
โดยที่ c เป็นค่าความแปรปรวนร่วมเกี่ยวของข้อมูลแต่ละมิติ ในที่นี้เพื่อความง่ายจะพิจารณาข้อมูลที่มีค่าเฉลี่ยอยู่ที่ 0 (เพียงแต่ในการใช้งานจริงต่อให้ไม่ปรับข้อมูลให้ค่าเฉลี่ยเป็น 0 ก็สามารถใช้ได้เหมือนกัน)
..(10)
โดยเลขที่ยกแล้วใส่วงเล็บอยู่ด้านบนคือดัชนีแสดงลำดับของข้อมูล บอกว่าเป็นจุดที่เท่าไหร่ ให้แยกแยะจากเลขด้านล่างซึ่งเป็นตัวบอกถึงมิติ
แล้วก็จะได้ว่า
..(11)
ในทำนองเดียวกัน เมทริกซ์ความแปรปรวนของพิกัดใหม่ก็จะสามารถเขียนได้เป็น
..(12)
หากแทนสมการสมการ (7) และ (8) แล้วจัดรูปจะได้ว่า
..(13)
ตรงนี้สาเหตุที่ VVT หายไปเพราะเป็นคุณสมบัติของเมทริกซ์เชิงตั้งฉาก
ทีนี้เป้าหมายของเราคือต้องการให้ระบบพิกัดใหม่แสดงการกระจายของข้อมูลตามแกนอย่างชัดเจนแยกจากกัน ดังนั้น Λ ควรเป็นเมทริกซ์แนวทแยง
..(14)
โดยที่ λ คือค่าความแปรปรวนของค่าต่างๆในพิกัดใหม่ ที่จริงต้องเป็นความแปรปรวนร่วมเกี่ยว λi,j แต่เนื่องจากเหลือแต่องค์ประกอบแนวทแยง คือ i=j กรณีนี้จะเป็นแค "ความแปรปรวน" เฉยๆ ไม่มี "ร่วมเกี่ยว" ในที่นี้เพื่อความง่ายก็เขียนเหลือแค่ λi
..(15)
แล้วฝั่งซ้ายของสมการ (13) ก็จะได้เป็น
..(16)
แบบนี้ก็จะได้ว่า
..(17)
ซึ่งเป็นรูปแบบของปัญหาการวิเคราะห์หาเวกเตอร์ลักษณะเฉพาะ (本征向量, eigenvector)
โดยในที่นี้ vi คือเวกเตอร์ลักษณะเฉพาะ C คือเมทริกซ์จตุรัส ส่วน λi คือค่าคงที่ เรียกว่าค่าลักษณะเฉพาะ (本征值, eigenvalue)
เกี่ยวกับเวกเตอร์ลักษณะเฉพาะในที่นี้จะไม่ลงรายละเอียด หากสนใจอาจอ่านเพิ่มได้ที่อื่นเช่นในวิกิ https://th.wikipedia.org/wiki/เวกเตอร์ลักษณะเฉพาะ
อนึ่ง คำว่า "ลักษณะเฉพาะ" ในที่นี้แปลจากคำว่า eigen ส่วน "ค่าแทนลักษณะ" ซึ่งหมายถึงตัวแปรต่างๆที่นำมาพิจารณานั้นแปลมาจากคำว่า feature เป็นคนละคำ คนละเรื่องกัน ดังนั้นต้องระวังอย่าจำสับสนกัน
เวกเตอร์ลักษณะเฉพาะคือเวกเตอร์ที่มีคุณสมบัติพิเศษคือเมื่อถูกคูณด้วยเมทริกซ์จตุรัสตัวนึงแล้วจะได้ผลออกมาเป็นค่าคงที่คูณกับเวกเตอร์ตัวเดิม
จากนั้นก็แก้สมการ (17) หาค่า λ และเวกเตอร์ v
..(18)
แล้วก็จะกลายเป็นปัญหา m สมการ โดยมีตัวแปรที่ไม่รู้อยู่ m+1 ตัว คือ v1,...vm และ λ
..(19)
ถ้าเป็นแบบนี้จะมีคำตอบได้ไม่จำกัด แต่เนื่องจากนี่เป็นเวกเตอร์สำหรับแปลงระบบพิกัด คุณสมบัติอย่างหนึ่งที่สำคัญก็คือขนาดจะต้องเป็น 1
..(20)
จากตรงนี้จึงมีสมการควบคุมเพิ่มอีกสมการ
เมื่อแก้สมการออกมาได้ก็จะพบว่ามีคู่ของเวกเตอร์และค่าลักษณะเฉพาะออกมาเป็นจำนวน m คู่ โดย v แต่ละตัวก็คือเวกเตอร์แสดงการแปลงพิกัดแกนที่เราต้องการ และ λ ที่เข้าคู่กับ v นั้นจะบอกถึงความแปรปรวนภายในแกนนั้น
ความแปรปรวนบอกถึงความสำคัญของแกนนั้น ปกติแล้วมักนำมาหารด้วยผลรวมของค่าความแปรปรวน แล้วเรียกว่า อัตราความบ่งบอกความแปรปรวน (解释方差占比, variance explained ratio)
..(21)
ค่านี้เองที่จะเป็นตัวที่พิจารณาว่าควรเก็บตัวแปรใหม่ตัวไหนไว้ ตัดตัวไหนทิ้ง ตัวที่ความแปรปรวนน้อยจะถูกตัดทิ้งได้ ดังนั้นสุดท้ายแล้วจำนวนแกนของระบบพิกัดใหม่ก็จะลดลงจากเดิม
วิธีการแก้สมการหาเวกเตอร์และค่าลักษณะเฉพาะจะไม่แสดงในนี้ แต่ว่า numpy มีฟังก์ชันสำหรับหาค่านี้ให้ นั่นคือ np.linalg.eig และ np.linalg.eigh ดังนั้นจะดึงมาใช้เลย
np.linalg.eig จะใช้กับเมทริกซ์ทั่วไปซึ่งค่าลักษณะเฉพาะที่ได้อาจไม่จำเป็นต้องเป็นจำนวนจริงเสมอไป แต่ np.linalg.eigh จะใช้กับเมทริกซ์แอร์มีต (埃尔米特矩阵, Hermitian matrix) ซึ่งเป็นเมทริกซ์ที่ค่าลักษณะเฉพาะทั้งหมดเป็นจำนวนจริงแน่นอน
ผลที่ได้จาก np.linalg.eigh จะเรียงลำดับตามค่าลักษณะเฉพาะเสมอ โดยเรียงจากน้อยไปมาก ในขณะที่ np.linalg.eig อาจไม่เรียงให้ ดังนั้นในที่นี้จะใช้ np.linalg.eigh
เขียนโปรแกรม
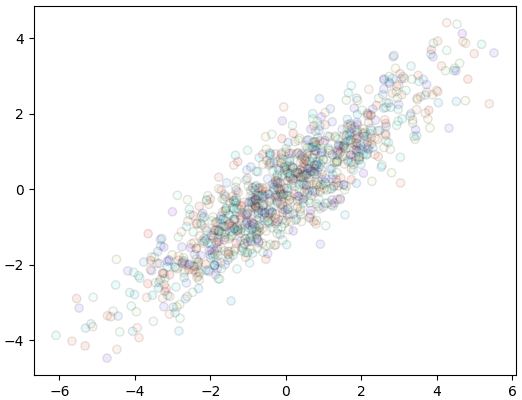
ขอยกตัวอย่างด้วยข้อมูลสองมิติ
คำนวณหาเมทริกซ์ความแปรปรวนร่วมเกี่ยว เสร็จแล้วก็หาเวกเตอร์ลักษณะเฉพาะดู
ได้
ฟังก์ชัน np.linalg.eig จะคืนค่ามา ๒ ตัว อันแรกคืออาเรย์ของค่าลักษณะเฉพาะทุกค่า อันหลังคืออาเรย์ซึ่งเอาเวกเตอร์ลักษณะเฉพาะมาเรียงต่อกันในแนวนอน
ในที่นี้มีสองมิติจึงได้อาเรย์ของเวกเตอร์เป็น 2x2 หลักทางซ้ายเป็นเวกเตอร์ตัวนึง ทางขวาเป็นอีกตัว
ลองแสดงทิศทางของแกนใหม่ที่ได้ภายในระบบพิกัดเดิมดู โดยคูณค่าลักษณะเฉพาะที่เข้าคู่กันไปด้วย เพื่อแสดงถึงขนาดความสำคัญ
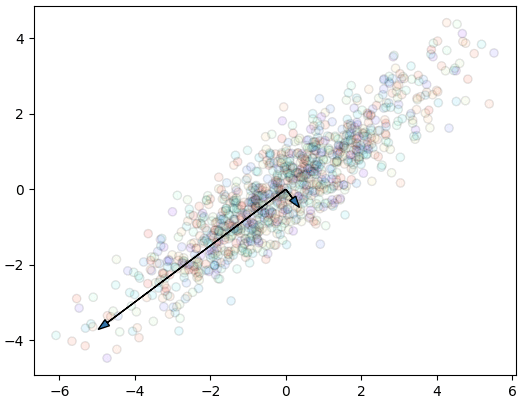
จะเห็นว่าแกนใหม่วางตัวตามการกระจายของข้อมูล ขนาดของแกนก็สอดคล้องกับการกระจาย
สำหรับการแปลงพิกัดไปอยู่ในแกนนี้สามารถทำได้ด้วยการคูณเมทริกซ์
ในที่สุดก็ได้จุดข้อมูลในระบบพิกัดใหม่
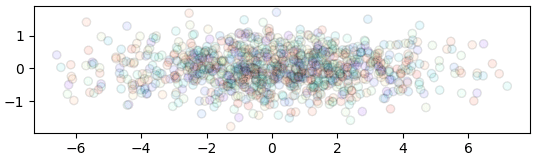
และหากนำข้อมูลนี้มาหาเมทริกซ์ความแปรปรวนร่วมเกี่ยวก็จะพบว่านอกจากแนวทแยงแล้วค่าแทบเป็น 0 คือการกระจายในแต่ละแกนเป็นอิสระต่อกัน ซึ่งตรงกับสิ่งที่ต้องการ
ได้
ต่อมาทีนี้ลองสร้างภาพแสดงความสัมพันธ์ระหว่างเมทริกซ์ความแปรปรวนร่วมเกี่ยวและเวกเตอร์ลักษณะเฉพาะที่หาได้ เพื่อให้เห็นภาพ
การสร้างกระจุกข้อมูลที่มีความแปรปรวนร่วมเกี่ยวตามที่ต้องการทำด้วยฟังก์ชัน multivariate_normal รายละเอียดได้แนะนำไปใน https://phyblas.hinaboshi.com/20180525
สร้างเป็นคลาส
กระบวนการตั้งแต่หาเมทริกซ์ความแปรปรวนร่วมเกี่ยว หาเวกเตอร์ลักษณะเฉพาะ และคูณเพื่อให้อยู่ในระบบพิกัดใหม่ อาจนำมาเขียนในรูปของคลาสเพื่อความสะดวกได้ดังนี้
การใช้ก็เริ่มจากสร้างออบเจ็กต์จากคลาสขึ้นมา แล้วก็ใส่ให้เรียนรู้ข้อมูลด้วยเมธอด .rianru() แล้วโปรแกรมก็จะคำนวณเวกเตอร์ลักษณะเฉพาะ (V) และอัตราความบ่งบอกความแปรปรวน (a) จากนั้นพอใช้เมธอด .plaeng() ก็จะเป็นการแปลงพิกัดของข้อมูลโดยคูณกับเวกเตอร์ลักษณะเฉพาะที่ได้มา
แต่ถ้าหากต้องการแปลงแค่ข้อมูลที่ใช้เรียนรู้แล้วให้คืนค่ามาทันทีก็อาจใช้เมธอด .rianru_plaeng() ก็จะเป็นการทำทั้ง rianru และ plaeng ไปเลยในคราวเดียว
ลองทดลองใช้กับข้อมูลสามมิติแบบนี้ (คำสั่ง make_blobs อ่านรายละเอียดได้ใน https://phyblas.hinaboshi.com/20161127)
ให้เรียนรู้แล้วหาค่าในระบบพิกัดใหม่ แสดงค่าในสองแกนแรกออกมา จะเห็นว่ามีการกระจายออกมาดี
คราวนี้ลองเปลี่ยนมาเป็นใช้สองแกนหลัง จะกลายเป็นว่าแกนหลังมีการกระจายน้อย
ดังนั้นแบบนี้ใช้แค่ ๒ แกนแรกในการวิเคราะห์ปัญหาก็เพียงพอ สามารถลดมิติของปัญหาลงได้
ทดลองใช้กับข้อมูลไวน์
เพื่อให้เห็นภาพชัดลองดูตัวอย่างของข้อมูลที่มีจำนวนมิติมาก ข้อมูลชุดหนึ่งที่นิยมถูกใช้เป็นตัวอย่างก็คือข้อมูลไวน์ ซึ่งก่อนหน้านี้ก็ได้เคยใช้ยกตัวอย่างไปแล้วใน https://phyblas.hinaboshi.com/20171207
จะได้ค่าอัตราความบ่งบอกความแปรปรวน
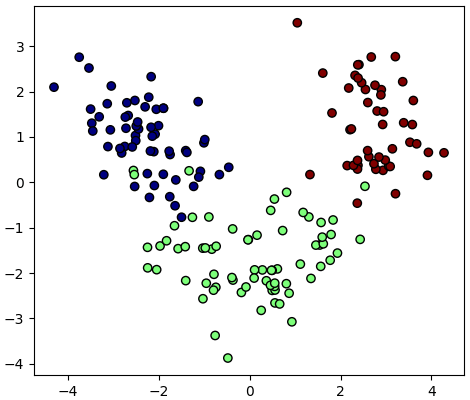
และนี่เป็นผลการวาดแสดงการกระจายตัวของค่าในสองแกนแรก
ความสำคัญของการทำข้อมูลให้เป็นมาตรฐาน
สิ่งหนึ่งที่ควรทำก่อนทำการวิเคราะห์องค์ประกอบหลักก็คือ ข้อมูลที่นำมาใช้นั้นหากตัวแปรต้นแต่ละตัวไม่ใช่หน่วยเดียวกันแล้วควรต้องปรับข้อมูลให้เป็นมาตรฐานก่อน เพราะมีผลมาก
เกี่ยวกับเรื่องการทำข้อมูลให้เป็นมาตรฐานเขียนไว้ใน https://phyblas.hinaboshi.com/20161124
จะเห็นว่าตัวอย่างข้อมูลไวน์ที่ใช้เมื่อครู่มีการแปลงค่าทำให้เป็นมาตรฐานก่อนที่จะนำมาใช้ด้วย
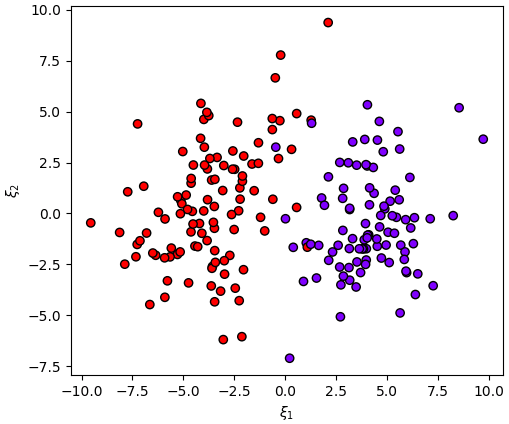
ตัวอย่างหนึ่งที่เห็นชัดคือเช่นข้อมูลลักษณะแบบนี้

จะเห็นว่าค่าแกนนอนมีขนาดใหญ่กว่าแกนตั้งมาก แบบนี้ต่อให้ทำการวิเคราะห์องค์ประกอบหลักก็จะได้แกนที่แทบไม่ต่างจากเดิม
แต่ถ้าทำข้อมูลให้เป็นมาตรฐานแล้วก็จะกลายเป็นแบบนี้ ผลที่ได้จะต่างออกไปมาก คราวนี้การย้ายแกนดูแล้วมีประโยชน์ขึ้นมาก
ส่วนผลการวิเคราะห์องค์ประกอบของไวน์นั้น หากไม่ทำข้อมูลให้เป็นมาตรฐานก่อนก็จะได้ผลเป็นแบบนี้แทน ซึ่งจะเห็นว่าผลต่างกันมาก

ดังนั้นจึงแสดงให้เห็นว่าถ้าไม่ทำข้อมูลให้เป็นมาตรฐานก่อน ถึงจะทำการวิเคราะห์องค์ประกอบหลักไปก็อาจไม่ได้ช่วยอะไร
การวิเคราะห์องค์ประกอบหลักด้วยการแยกค่าเอกฐาน (SVD)
ในทางปฏิบัติแล้ว แทนที่จะคำนวณหาเวกเตอร์ลักษณะเฉพาะของเมทริกซ์คามแปรปรวนร่วมเกี่ยว วิธีที่มักใช้แทนคือใช้วิธีการแยกค่าเอกฐาน (SVD)
รายละเอียดเขียนไว้ในบทความนี้ https://phyblas.hinaboshi.com/20190916
อ้างอิง
การพิจารณาตัวแปรที่ไม่จำเป็นเยอะเกินจำเป็นอาจทำให้เกิดปัญหาการเรียนรู้เกิน (过学习, overlearning)
ก่อนหน้านี้ได้แนะนำเรื่องการลดตัวแปรของปัญหาในการเรียนรู้ของเครื่องด้วยวิธีการคัดเลือกค่าแทนลักษณะ (特征选择, feature selection) https://phyblas.hinaboshi.com/20171211
อย่างไรก็ตาม นั่นเป็นเพียงแค่การคัดเลือกตัวแปรจากเดิมทีที่มีอยู่แล้วว่าตัวไหนจำเป็นและตัดบางตัวทิ้งเท่านั้น
แต่มีอีกแนวทางหนึ่งที่อาจจะได้ผลดีกว่า ก็คือสร้างชุดตัวแปรใหม่ขึ้นจากชุดตัวแปรเดิมที่มีอยู่
วิธีการหนึ่งที่เป็นที่นิยมก็คือ การวิเคราะห์องค์ประกอบหลัก (主成分分析, principle component Analysis) หรือนิยมเรียกย่อว่า PCA
แนวคิด
การวิเคราะห์องค์ประกอบหลักคือการเอาข้อมูลซึ่งอยู่ในระบบพิกัดของชุดตัวแปรเดิมมาแปลงให้อยู่ในรูปของชุดตัวแปรใหม่ โดยเมื่อแปลงเสร็จแล้วตัวแปรใหม่จะมีทั้งที่สำคัญและไม่สำคัญก็ตัดตัวที่ไม่สำคัญทิ้งไป
ยกตัวอย่างเช่นมีข้อมูลสามมิติที่มีการแจกแจงตามนี้

พอพลิกแกนดูในแนวนึงจะเห็นว่ามันวางตัวเกือบจะเป็นแผ่นจานแบน

แบบนั้นแล้วหากเราแค่พิจารณาค่าแค่ตามแนวระนาบสองมิติก็น่าจะพอ
การที่จะพิจารณาข้อมูลตามแนวนั้นได้สะดวกก็คือ ทำการย้ายพิกัด สร้างแกนใหม่ให้วางแนวตามนี้

แล้วพอหมุนเปลี่ยนระบบพิกัดมาเป็นตามแกนนั้นก็จะกลายเป็นแบบนี้

เท่านี้ก็จะสามารถละแกนตั้งทิ้งไปได้เลย แล้วเขียนเป็นสองมิติได้แบบนี้

นี่คือแนวคิดของการวิเคราะห์องค์ประกอบหลัก คือตั้งระบบพิกัดใหม่ หาแกนที่มีการกระจายตัวสูง แล้วตัดเอาแกนที่มีการกระจายตัวต่ำทิ้ง ช่วยลดจำนวนมิติของข้อมูลได้
วิธีการ
ในการแปลงระบบพิกัดนั้นวิธีพื้นฐานที่ง่ายที่สุดคือการแปลงเชิงเส้น คือเขียนระบบพิกัดใหม่โดยคำนวณจาก
..(1)
โดยในที่นี้ใช้ ξ1,ξ2,... แทนระบบพิกัดใหม่ ส่วน x1,x2,... แทนระบบพิกัดเดิม มีจำนวน m มิติ แต่ละตัวมีคุณสมบัติตั้งฉาก (正交, orthogonal)
v คือค่าน้ำหนักในการแปลง
เขียนค่าพิกัดใหม่แต่ละตัวในรูปเวกเตอร์ได้แบบนี้
..(2)
เอาองค์ประกอบทั้งหมดมาเขียนในรูปเมทริกซ์ก็จะได้แบบนี้
..(3)
โดย
..(4)
..(5)
โดย V เป็นเมทริกซ์เชิงตั้งฉาก (正交矩阵, orthogonal matrix) รวบรวมค่าน้ำหนักทั้งหมดในการแปลง
..(6)
ในบทความนี้จะใช้สัญลักษณ์ลูกศรบนหัวแทนเวกเตอร์ (= เมทริกซ์มิติเดียว) ส่วนอักษรตัวหนาแทนเมทริกซ์สองมิติ ถ้าอักษรตัวเอียงธรรมดาจะแทนเลขเดี่ยว
ดังนั้นระบบพิกัดใหม่เขียนสั้นๆได้เป็น
..(7)
หรือเขียนใหม่แสดงเป็นเมทริกซ์ในแนวตั้งก็เป็น (จากสมบัติของเมทริกซ์)
..(8)
ทีนี้เป้าหมายก็คือหาว่าเมทริกซ์ V ควรจะหน้าตาเป็นยังไง
เป้าหมายของเราคือการหาแกนใหม่ตามขนาดการกระจายตัวของข้อมูล ดังนั้นสิ่งที่ควรจะพิจารณาก็คือ ความแปรปรวนร่วมเกี่ยว (协方差, covariance) ของข้อมูล
เกี่ยวเรื่องความแปรปรวนร่วมเกี่ยวได้เขียนถึงไว้แล้วใน https://phyblas.hinaboshi.com/20180517
เมทริกซ์ความแปรปรวนร่วมเกี่ยวแสดงได้โดย
..(9)
โดยที่ c เป็นค่าความแปรปรวนร่วมเกี่ยวของข้อมูลแต่ละมิติ ในที่นี้เพื่อความง่ายจะพิจารณาข้อมูลที่มีค่าเฉลี่ยอยู่ที่ 0 (เพียงแต่ในการใช้งานจริงต่อให้ไม่ปรับข้อมูลให้ค่าเฉลี่ยเป็น 0 ก็สามารถใช้ได้เหมือนกัน)
..(10)
โดยเลขที่ยกแล้วใส่วงเล็บอยู่ด้านบนคือดัชนีแสดงลำดับของข้อมูล บอกว่าเป็นจุดที่เท่าไหร่ ให้แยกแยะจากเลขด้านล่างซึ่งเป็นตัวบอกถึงมิติ
แล้วก็จะได้ว่า
..(11)
ในทำนองเดียวกัน เมทริกซ์ความแปรปรวนของพิกัดใหม่ก็จะสามารถเขียนได้เป็น
..(12)
หากแทนสมการสมการ (7) และ (8) แล้วจัดรูปจะได้ว่า
..(13)
ตรงนี้สาเหตุที่ VVT หายไปเพราะเป็นคุณสมบัติของเมทริกซ์เชิงตั้งฉาก
ทีนี้เป้าหมายของเราคือต้องการให้ระบบพิกัดใหม่แสดงการกระจายของข้อมูลตามแกนอย่างชัดเจนแยกจากกัน ดังนั้น Λ ควรเป็นเมทริกซ์แนวทแยง
..(14)
โดยที่ λ คือค่าความแปรปรวนของค่าต่างๆในพิกัดใหม่ ที่จริงต้องเป็นความแปรปรวนร่วมเกี่ยว λi,j แต่เนื่องจากเหลือแต่องค์ประกอบแนวทแยง คือ i=j กรณีนี้จะเป็นแค "ความแปรปรวน" เฉยๆ ไม่มี "ร่วมเกี่ยว" ในที่นี้เพื่อความง่ายก็เขียนเหลือแค่ λi
..(15)
แล้วฝั่งซ้ายของสมการ (13) ก็จะได้เป็น
..(16)
แบบนี้ก็จะได้ว่า
..(17)
ซึ่งเป็นรูปแบบของปัญหาการวิเคราะห์หาเวกเตอร์ลักษณะเฉพาะ (本征向量, eigenvector)
โดยในที่นี้ vi คือเวกเตอร์ลักษณะเฉพาะ C คือเมทริกซ์จตุรัส ส่วน λi คือค่าคงที่ เรียกว่าค่าลักษณะเฉพาะ (本征值, eigenvalue)
เกี่ยวกับเวกเตอร์ลักษณะเฉพาะในที่นี้จะไม่ลงรายละเอียด หากสนใจอาจอ่านเพิ่มได้ที่อื่นเช่นในวิกิ https://th.wikipedia.org/wiki/เวกเตอร์ลักษณะเฉพาะ
อนึ่ง คำว่า "ลักษณะเฉพาะ" ในที่นี้แปลจากคำว่า eigen ส่วน "ค่าแทนลักษณะ" ซึ่งหมายถึงตัวแปรต่างๆที่นำมาพิจารณานั้นแปลมาจากคำว่า feature เป็นคนละคำ คนละเรื่องกัน ดังนั้นต้องระวังอย่าจำสับสนกัน
เวกเตอร์ลักษณะเฉพาะคือเวกเตอร์ที่มีคุณสมบัติพิเศษคือเมื่อถูกคูณด้วยเมทริกซ์จตุรัสตัวนึงแล้วจะได้ผลออกมาเป็นค่าคงที่คูณกับเวกเตอร์ตัวเดิม
จากนั้นก็แก้สมการ (17) หาค่า λ และเวกเตอร์ v
..(18)
แล้วก็จะกลายเป็นปัญหา m สมการ โดยมีตัวแปรที่ไม่รู้อยู่ m+1 ตัว คือ v1,...vm และ λ
..(19)
ถ้าเป็นแบบนี้จะมีคำตอบได้ไม่จำกัด แต่เนื่องจากนี่เป็นเวกเตอร์สำหรับแปลงระบบพิกัด คุณสมบัติอย่างหนึ่งที่สำคัญก็คือขนาดจะต้องเป็น 1
..(20)
จากตรงนี้จึงมีสมการควบคุมเพิ่มอีกสมการ
เมื่อแก้สมการออกมาได้ก็จะพบว่ามีคู่ของเวกเตอร์และค่าลักษณะเฉพาะออกมาเป็นจำนวน m คู่ โดย v แต่ละตัวก็คือเวกเตอร์แสดงการแปลงพิกัดแกนที่เราต้องการ และ λ ที่เข้าคู่กับ v นั้นจะบอกถึงความแปรปรวนภายในแกนนั้น
ความแปรปรวนบอกถึงความสำคัญของแกนนั้น ปกติแล้วมักนำมาหารด้วยผลรวมของค่าความแปรปรวน แล้วเรียกว่า อัตราความบ่งบอกความแปรปรวน (解释方差占比, variance explained ratio)
..(21)
ค่านี้เองที่จะเป็นตัวที่พิจารณาว่าควรเก็บตัวแปรใหม่ตัวไหนไว้ ตัดตัวไหนทิ้ง ตัวที่ความแปรปรวนน้อยจะถูกตัดทิ้งได้ ดังนั้นสุดท้ายแล้วจำนวนแกนของระบบพิกัดใหม่ก็จะลดลงจากเดิม
วิธีการแก้สมการหาเวกเตอร์และค่าลักษณะเฉพาะจะไม่แสดงในนี้ แต่ว่า numpy มีฟังก์ชันสำหรับหาค่านี้ให้ นั่นคือ np.linalg.eig และ np.linalg.eigh ดังนั้นจะดึงมาใช้เลย
np.linalg.eig จะใช้กับเมทริกซ์ทั่วไปซึ่งค่าลักษณะเฉพาะที่ได้อาจไม่จำเป็นต้องเป็นจำนวนจริงเสมอไป แต่ np.linalg.eigh จะใช้กับเมทริกซ์แอร์มีต (埃尔米特矩阵, Hermitian matrix) ซึ่งเป็นเมทริกซ์ที่ค่าลักษณะเฉพาะทั้งหมดเป็นจำนวนจริงแน่นอน
ผลที่ได้จาก np.linalg.eigh จะเรียงลำดับตามค่าลักษณะเฉพาะเสมอ โดยเรียงจากน้อยไปมาก ในขณะที่ np.linalg.eig อาจไม่เรียงให้ ดังนั้นในที่นี้จะใช้ np.linalg.eigh
เขียนโปรแกรม
ขอยกตัวอย่างด้วยข้อมูลสองมิติ
import numpy as np
import matplotlib.pyplot as plt
x = np.random.normal(0,2,1000)
y = np.random.normal(x*0.7,0.7)
c = np.random.random(1000) # ใส่สีเพื่อความสวยงามเฉยๆ ไม่มีความหมายอะไร
plt.axes(aspect=1)
plt.scatter(x,y,c=c,edgecolor='k',alpha=0.1,cmap='rainbow')
plt.show()
คำนวณหาเมทริกซ์ความแปรปรวนร่วมเกี่ยว เสร็จแล้วก็หาเวกเตอร์ลักษณะเฉพาะดู
praeruam = np.cov(x,y)
print('เมทริกซ์ความแปรปรวนร่วมเกี่ยว\n',praeruam)
kha_eig,vec_eig = np.linalg.eigh(praeruam)
print('ค่าลักษณะเฉพาะ\n',kha_eig)
print('เวกเตอร์ลักษณะเฉพาะ\n',vec_eig)ได้
เมทริกซ์ความแปรปรวนร่วมเกี่ยว
[[3.90083866 2.68839157]
[2.68839157 2.31209055]]
ค่าลักษณะเฉพาะ
[0.30316666 5.90976256]
เวกเตอร์ลักษณะเฉพาะ
[[ 0.59859366 -0.80105282]
[-0.80105282 -0.59859366]]ฟังก์ชัน np.linalg.eig จะคืนค่ามา ๒ ตัว อันแรกคืออาเรย์ของค่าลักษณะเฉพาะทุกค่า อันหลังคืออาเรย์ซึ่งเอาเวกเตอร์ลักษณะเฉพาะมาเรียงต่อกันในแนวนอน
ในที่นี้มีสองมิติจึงได้อาเรย์ของเวกเตอร์เป็น 2x2 หลักทางซ้ายเป็นเวกเตอร์ตัวนึง ทางขวาเป็นอีกตัว
ลองแสดงทิศทางของแกนใหม่ที่ได้ภายในระบบพิกัดเดิมดู โดยคูณค่าลักษณะเฉพาะที่เข้าคู่กันไปด้วย เพื่อแสดงถึงขนาดความสำคัญ
kaen_x_mai = kha_eig[1]*vec_eig[:,1]
kaen_y_mai = kha_eig[0]*vec_eig[:,0]
plt.axes(aspect=1)
plt.scatter(x,y,c=c,edgecolor='k',alpha=0.1,cmap='rainbow')
plt.arrow(0,0,kaen_x_mai[0],kaen_x_mai[1],head_width=0.2)
plt.arrow(0,0,kaen_y_mai[0],kaen_y_mai[1],head_width=0.2)
plt.show()
จะเห็นว่าแกนใหม่วางตัวตามการกระจายของข้อมูล ขนาดของแกนก็สอดคล้องกับการกระจาย
สำหรับการแปลงพิกัดไปอยู่ในแกนนี้สามารถทำได้ด้วยการคูณเมทริกซ์
X = np.array([x,y]).T
Xi = X.dot(vec_eig[:,::-1])
xi,yi = Xi.T
plt.axes(aspect=1)
plt.scatter(xi,yi,c=c,edgecolor='k',alpha=0.1,cmap='rainbow')
plt.show()ในที่สุดก็ได้จุดข้อมูลในระบบพิกัดใหม่

และหากนำข้อมูลนี้มาหาเมทริกซ์ความแปรปรวนร่วมเกี่ยวก็จะพบว่านอกจากแนวทแยงแล้วค่าแทบเป็น 0 คือการกระจายในแต่ละแกนเป็นอิสระต่อกัน ซึ่งตรงกับสิ่งที่ต้องการ
print(np.cov(xi,yi))ได้
[[5.90976256e+00 1.58698546e-16]
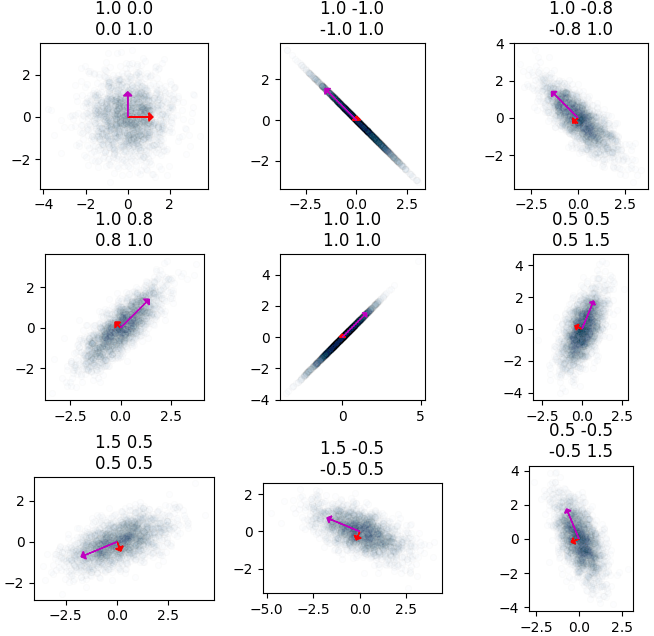
[1.58698546e-16 3.03166658e-01]]ต่อมาทีนี้ลองสร้างภาพแสดงความสัมพันธ์ระหว่างเมทริกซ์ความแปรปรวนร่วมเกี่ยวและเวกเตอร์ลักษณะเฉพาะที่หาได้ เพื่อให้เห็นภาพ
cov = np.array([[[1,0],[0,1]],
[[1,-1],[-1,1]],
[[1,-0.8],[-0.8,1]],
[[1,0.8],[0.8,1]],
[[1,1],[1,1]],
[[0.5,0.5],[0.5,1.5]],
[[1.5,0.5],[0.5,0.5]],
[[1.5,-0.5],[-0.5,0.5]],
[[0.5,-0.5],[-0.5,1.5]],
])
plt.figure(figsize=[7,8])
for i,c in enumerate(cov):
x,y = np.random.multivariate_normal([0,0],c,2000).T
X = np.array([x,y]).T
kha_eig,vec_eig = np.linalg.eigh(c)
plt.subplot(331+i,aspect=1)
plt.scatter(x,y,s=20,edgecolor='k',alpha=0.01)
plt.title('%.1f %.1f\n%.1f %.1f'%(c[0,0],c[0,1],c[1,0],c[1,1]))
kv = kha_eig*vec_eig
plt.arrow(0,0,kv[0,0],kv[1,0],color='r',head_width=0.4,head_length=0.2)
plt.arrow(0,0,kv[0,1],kv[1,1],color='m',head_width=0.4,head_length=0.2)
plt.tight_layout()
plt.show()
การสร้างกระจุกข้อมูลที่มีความแปรปรวนร่วมเกี่ยวตามที่ต้องการทำด้วยฟังก์ชัน multivariate_normal รายละเอียดได้แนะนำไปใน https://phyblas.hinaboshi.com/20180525
สร้างเป็นคลาส
กระบวนการตั้งแต่หาเมทริกซ์ความแปรปรวนร่วมเกี่ยว หาเวกเตอร์ลักษณะเฉพาะ และคูณเพื่อให้อยู่ในระบบพิกัดใหม่ อาจนำมาเขียนในรูปของคลาสเพื่อความสะดวกได้ดังนี้
class WikhroOngprakopLak:
def rianru(self,X):
praeruam = np.cov(X.T)
kha_eig,vec_eig = np.linalg.eigh(praeruam)
self.V = vec_eig[:,::-1]
self.a = kha_eig[::-1]/kha_eig.sum()
def plaeng(self,X):
return X.dot(self.V)
def rianru_plaeng(self,X):
self.rianru(X)
return self.plaeng(X)การใช้ก็เริ่มจากสร้างออบเจ็กต์จากคลาสขึ้นมา แล้วก็ใส่ให้เรียนรู้ข้อมูลด้วยเมธอด .rianru() แล้วโปรแกรมก็จะคำนวณเวกเตอร์ลักษณะเฉพาะ (V) และอัตราความบ่งบอกความแปรปรวน (a) จากนั้นพอใช้เมธอด .plaeng() ก็จะเป็นการแปลงพิกัดของข้อมูลโดยคูณกับเวกเตอร์ลักษณะเฉพาะที่ได้มา
แต่ถ้าหากต้องการแปลงแค่ข้อมูลที่ใช้เรียนรู้แล้วให้คืนค่ามาทันทีก็อาจใช้เมธอด .rianru_plaeng() ก็จะเป็นการทำทั้ง rianru และ plaeng ไปเลยในคราวเดียว
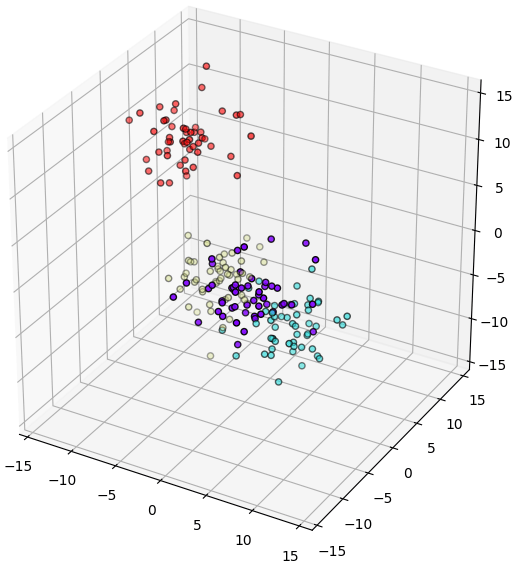
ลองทดลองใช้กับข้อมูลสามมิติแบบนี้ (คำสั่ง make_blobs อ่านรายละเอียดได้ใน https://phyblas.hinaboshi.com/20161127)
from sklearn import datasets
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(10)
X,z = datasets.make_blobs(200,n_features=3,centers=4,cluster_std=2.5)
mm = X.min(),X.max()
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=mm,ylim=mm,zlim=mm)
ax.scatter(X[:,0],X[:,1],X[:,2],c=z,cmap='rainbow',edgecolor='k')
plt.show()
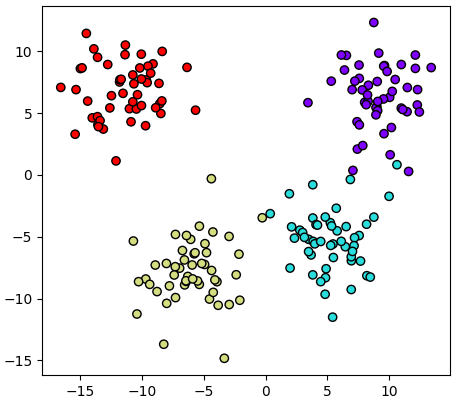
ให้เรียนรู้แล้วหาค่าในระบบพิกัดใหม่ แสดงค่าในสองแกนแรกออกมา จะเห็นว่ามีการกระจายออกมาดี
wol = WikhroOngprakopLak()
wol.rianru(X)
Xi = wol.plaeng(X)
# หรือ Xi = WikhroOngprakopLak().rianru_plaeng(X)
plt.axes(aspect=1)
plt.scatter(Xi[:,0],Xi[:,1],c=z,cmap='rainbow',edgecolor='k')
plt.show()
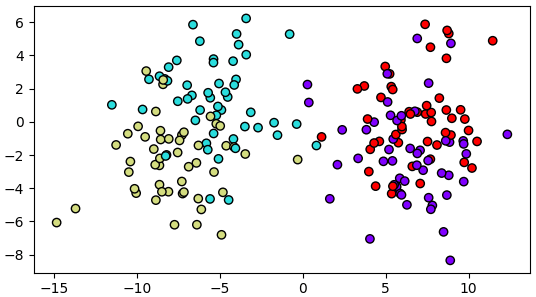
คราวนี้ลองเปลี่ยนมาเป็นใช้สองแกนหลัง จะกลายเป็นว่าแกนหลังมีการกระจายน้อย
plt.axes(aspect=1)
plt.scatter(Xi[:,1],Xi[:,2],c=z,cmap='rainbow',edgecolor='k')
plt.show()
ดังนั้นแบบนี้ใช้แค่ ๒ แกนแรกในการวิเคราะห์ปัญหาก็เพียงพอ สามารถลดมิติของปัญหาลงได้
ทดลองใช้กับข้อมูลไวน์
เพื่อให้เห็นภาพชัดลองดูตัวอย่างของข้อมูลที่มีจำนวนมิติมาก ข้อมูลชุดหนึ่งที่นิยมถูกใช้เป็นตัวอย่างก็คือข้อมูลไวน์ ซึ่งก่อนหน้านี้ก็ได้เคยใช้ยกตัวอย่างไปแล้วใน https://phyblas.hinaboshi.com/20171207
w = datasets.load_wine()
X,z = w.data,w.target
X = (X-X.mean(0))/X.std(0) # แปลงข้อมูลให้เป็นมาตรฐาน
wol = WikhroOngprakopLak()
Xi = wol.rianru_plaeng(X)
print(wol.a) # แสดงค่าอัตราความบ่งบอกความแปรปรวน
# แสดงการกระจายตัวของสองแกนแรก
plt.axes(aspect=1)
plt.scatter(Xi[:,0],Xi[:,1],c=z,cmap='jet',edgecolor='k')
plt.show()จะได้ค่าอัตราความบ่งบอกความแปรปรวน
[ 0.36198848 0.1920749 0.11123631 0.0706903 0.06563294 0.04935823
0.04238679 0.02680749 0.02222153 0.01930019 0.01736836 0.01298233
0.00795215]และนี่เป็นผลการวาดแสดงการกระจายตัวของค่าในสองแกนแรก

ความสำคัญของการทำข้อมูลให้เป็นมาตรฐาน
สิ่งหนึ่งที่ควรทำก่อนทำการวิเคราะห์องค์ประกอบหลักก็คือ ข้อมูลที่นำมาใช้นั้นหากตัวแปรต้นแต่ละตัวไม่ใช่หน่วยเดียวกันแล้วควรต้องปรับข้อมูลให้เป็นมาตรฐานก่อน เพราะมีผลมาก
เกี่ยวกับเรื่องการทำข้อมูลให้เป็นมาตรฐานเขียนไว้ใน https://phyblas.hinaboshi.com/20161124
จะเห็นว่าตัวอย่างข้อมูลไวน์ที่ใช้เมื่อครู่มีการแปลงค่าทำให้เป็นมาตรฐานก่อนที่จะนำมาใช้ด้วย
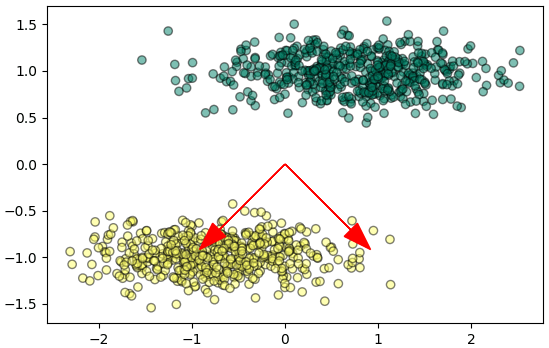
ตัวอย่างหนึ่งที่เห็นชัดคือเช่นข้อมูลลักษณะแบบนี้

จะเห็นว่าค่าแกนนอนมีขนาดใหญ่กว่าแกนตั้งมาก แบบนี้ต่อให้ทำการวิเคราะห์องค์ประกอบหลักก็จะได้แกนที่แทบไม่ต่างจากเดิม
แต่ถ้าทำข้อมูลให้เป็นมาตรฐานแล้วก็จะกลายเป็นแบบนี้ ผลที่ได้จะต่างออกไปมาก คราวนี้การย้ายแกนดูแล้วมีประโยชน์ขึ้นมาก

ส่วนผลการวิเคราะห์องค์ประกอบของไวน์นั้น หากไม่ทำข้อมูลให้เป็นมาตรฐานก่อนก็จะได้ผลเป็นแบบนี้แทน ซึ่งจะเห็นว่าผลต่างกันมาก

ดังนั้นจึงแสดงให้เห็นว่าถ้าไม่ทำข้อมูลให้เป็นมาตรฐานก่อน ถึงจะทำการวิเคราะห์องค์ประกอบหลักไปก็อาจไม่ได้ช่วยอะไร
การวิเคราะห์องค์ประกอบหลักด้วยการแยกค่าเอกฐาน (SVD)
ในทางปฏิบัติแล้ว แทนที่จะคำนวณหาเวกเตอร์ลักษณะเฉพาะของเมทริกซ์คามแปรปรวนร่วมเกี่ยว วิธีที่มักใช้แทนคือใช้วิธีการแยกค่าเอกฐาน (SVD)
รายละเอียดเขียนไว้ในบทความนี้ https://phyblas.hinaboshi.com/20190916
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib