numpy & matplotlib เบื้องต้น บทที่ ๓๐: ความชันและอนุพันธ์เชิงตัวเลข
เขียนเมื่อ 2016/06/12 12:11
แก้ไขล่าสุด 2021/09/28 16:42
ใน numpy มีฟังก์ชันที่ช่วยในการหาอนุพันธ์เชิงตัวเลขอยู่ในตัว ในที่นี้จะมาพูดถึงกันเล็กน้อยแค่ในระดับที่เข้าใจได้ง่ายไม่ลงลึก
การหาค่าความเปลี่ยนแปลงของสมาชิกแต่ละตัวในอาเรย์ด้วย np.diff
การหาอนุพันธ์เชิงตัวเลขอย่างง่ายสุดก็คือการคำนวณค่าความเปลี่ยนแปลงระหว่างสมาชิกแต่ละตัวในอาเรย์
ถ้าลองทำโดยใช้ for ก็จะเป็น
แต่เราสามารถทำได้ง่ายกว่านั้นด้วยการอาเรย์ตัวนี้ที่ตัดส่วนหัวกับที่ตัดส่วนท้ายมาลบกัน นั่นคือ y[1:]-y[:-1]
แต่มีฟังก์ชันที่ไว้ใช้เพื่อการนั้นโดยเฉพาะ นั่นคือ np.diff
หากต้องการอาอนุพันธ์อันดับสองขึ้นไปก็ทำได้โดยการใส่อาร์กิวเมนต์ตัวที่สองลงไป
อันนี้เป็นเพราะว่าอนุพันธ์อันดับหนึ่งเท่ากันหมด ดังนั้นอันดับสองจึงเป็น 0
หากลองใหม่เป็นค่าที่มาจากฟังก์ชันยกกำลังสองจะได้อาเรย์ที่มีค่าไม่เป็น 0 ไปจนถึงอันดับที่สอง
ฟังก์ชันนี้ตรงกันข้ามกันกับ np.cumsum ซึ่งเคยกล่าวถึงไปแล้วในบทที่ ๑๗ ดังนั้นหากใช้ฟังก์ชันนี้กับฟังก์ชันที่ได้จาก np.cumsum ก็จะได้ผลใกล้เคียงอาเรย์เดิม
ตัวอย่าง
จะเห็นว่าผลที่ได้จากการ np.cumsum แล้ว np.diff หรือ np.diff แล้วค่อย np.cumsum จะออกมาคล้ายตัวเดิมแต่มีสมาชิกหายไปตัวหนึ่ง
นั่นเพราะว่าเวลาใช้ np.diff แล้วจำนวนสมาชิกจะลดลงไปตัวหนึ่งเสมอ นั่นก็เป็นข้อเสียของฟังก์ชันนี้
และสิ่งที่ np.diff คำนวณได้นั้นคือความต่างของค่าของสมาชิกทีละตัว ในกรณีที่สมาชิกในแต่ละตัวนั้นแทนค่าของฟังก์ชัน f(x) ที่ x = 1,2,3 ตามลำดับไปเรื่อยๆค่าที่ได้จาก np.diff ก็จะเป็นค่าอนุพันธ์โดยประมาณทันที แต่โดยทั่วไประยะห่างระหว่างค่า x แต่ละค่าอาจเป็นจำนวนใดๆซึ่งยิ่งเล็กก็ยิ่งดี
การคำนวณของ np.diff นั้นเป็นการหาอนุพันธ์ในรูปแบบของสูตรผลต่างแบบไปข้างหน้าที่มีความแม่น อันดับหนึ่ง ซึ่งหากเขียนเป็นสมการก็จะได้ว่า
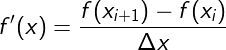
แต่อย่างที่เห็นก็คือ np.diff แค่เอาค่าในลำดับต่อกันมาลบกันเฉยๆ ไม่ได้หาร Δx ดังนั้นหากเรารู้ค่า Δx จริงๆว่าเป็นเท่าไหร่ก็เอาค่านั้นไปหารจึงจะได้ค่าอนุพันธ์ที่แท้จริง
อย่างไรก็ตาม สำหรับการคำนวณหาอนุพันธ์ที่ดีกว่านั้นเราอาจควรเลือกใช้ฟังก์ชันอีกตัวหนึ่ง นั่นคือ np.gradient
การหาอนุพันธ์ด้วย np.gradient
np.gradient เป็นฟังก์ชันสำหรับหาอนุพันธ์เชิงตัวเลขของอาเรย์โดยใช้สูตรผลต่างแบบตรงกลางที่มีความแม่นอันดับสอง นั่นคือ
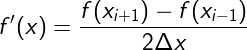
ซึ่งจะมีความแม่นยำมากกว่า np.diff ซึ่งใช้สูตรผลต่างแบบไปข้างหน้าที่มีความแม่นอันดับหนึ่ง เพราะว่านำทั้งตัวหน้าและตัวหลังมาคิด
เพียงแต่ว่าค่าตัวแรกสุดจะไม่มีค่าก่อนหน้ามัน (i-1) ดังนั้นจึงได้แต่ใช้สูตรผลต่างแบบไปข้างหน้าที่มีความแม่นอันดับหนึ่งเช่น เดียวกับ np.diff ดังนั้นตัวแรกของ np.diff และ np.gradient ควรจะได้ค่าเหมือนกัน
ส่วนค่าตัวสุดท้ายจะไม่มีตัวที่อยู่หลังมัน (i+1) ดังนั้นจึงต้องใช้สูตรผลต่างแบบย้อนกลับที่มีความแม่นอันดับหนึ่ง นั่นคือ
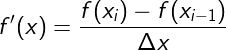
ตัวอย่างการใช้ ลองหาอนุพันธ์ของ x กำลัง 3 ด้วยวิธีนี้แล้วเทียบกับกราฟอนุพันธ์จริงๆซึ่งควรเป็น 3x**2
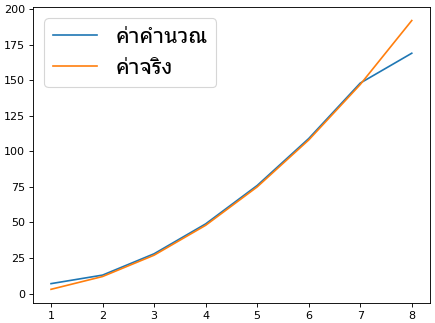
เห็นได้ชัดว่ามีความคลาดเคลื่อน ซึ่งยังไงก็หลีกเลี่ยงไม่ได้ โดยเฉพาะที่ปลาย
เพื่อความแม่นยำมากขึ้นเราสามารถกำหนดให้ที่ปลายทั้งสองข้างใช้การหาอนุพันธ์โดย สูตรผลต่างที่มีความแม่นยำอันดับสองได้โดยเพิ่มคีย์เวิร์ด edge_order=2
แบบนี้แล้วที่ตัวแรกจะเป็นการคำนวณโดยใช้สูตรผลต่างแบบไปข้างหน้าที่มีความแม่น อันดับสอง นั่นคือนอกจากจะเอาค่าที่ตำแหน่งนั้น (i) และตำแหน่งถัดไป (i+1) แล้วยังนำตำแหน่งถัดจากนั้นไปอีก (i+2) มาคิดด้วย
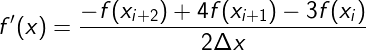
สัมประสิทธิ์ที่เป็น 4 และ 3 ที่เห็นด้านหน้านี้มาจากการคิดโดยอนุกรมเทย์เลอร์
ส่วนตัวสุดท้ายจะกลับกัน คือเอาที่ตำแหน่งนั้น (i) และตำแหน่งก่อนหน้านั้น (i-1) และก่อนหน้านั้นไปอีก (i-2)
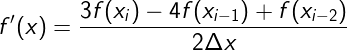
ลองทำดูใหม่โดยใส่ edge_order=2 จะได้เป็น
จะเห็นได้ว่าค่าที่ขอบปลายทั้งสองข้างเปลี่ยนไปโดยใกล้เคียงกว่าเดิม แม้จะยังคงมีความคลาดเคลื่อนอยู่
การคำนวณเชิงตัวเลขนั้นยังไงความคลาดเคลื่อนก็เป็นสิ่งที่หลีกเลี่ยงไม่ได้อยู่ แล้ว แต่ว่ายิ่งค่าที่ใช้คำนวณมีความละเอียดเท่าไหร่ความคลาดเคลื่อนก็จะยิ่งน้อย ลงเท่านั้น ในการใช้งานจริงๆมักจะใช้ค่า Δx เล็กมากๆเพื่อให้ความคลาดเคลื่อนต่ำจนอยู่ในระดับที่ยอมรับได้
ในตัวอย่างข้างต้นนี้เราไม่ได้กำหนดค่า Δx ดังนั้นจึงถือว่า Δx เป็น 1 ไปโดยปริยาย แต่เราสามารถกำหนดค่า Δx ได้โดยใส่ลงไปเป็นอาร์กิวเมนต์ตัวที่สอง
ลองทำกับฟังก์ชันเดิม แต่เพิ่มความละเอียดโดย Δx เป็น 0.01
อนุพันธ์ย่อย
ในตัวอย่างที่ผ่านๆมาเราใช้ np.gradient และ np.diff กับอาเรย์หนึ่งมิติ แต่ที่จริงแล้วทั้งสองฟังก์ชันนี้จะใช้กับอาเรย์กี่มิติก็ได้
หากใช้กับอาเรย์สองมิติขึ้นไป สิ่งที่หาได้ก็จะเป็นอนุพันธ์ย่อย นั่นคืออนุพันธ์ของค่า f(x,y) เมื่อเทียบกับ x หรือ y แยกกัน
ค่าคืนกลับที่ได้จาก np.gradient ในกรณีสองมิติจะออกมาเป็นลิสต์ที่มีสมาชิกอยู่สองตัว คือค่าอนุพันธ์ย่อยในแกน y และ x
ตัวอย่างเช่น พิจารณาฟังก์ชัน z = x**2 + y**2 - 9 ซึ่งหากคำนวณก็จะได้ผลออกมาตามนี้
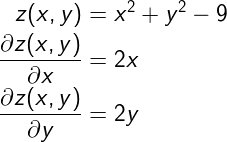
คราวนี้มาลองหาโดยใช้ np.gradient ดู
ได้
กรณีที่จะระบุค่า Δx และ Δy ก็ให้ใส่เป็นอาร์กิวเมนต์ต่อกันไป
ลองนำมาวาดเป็นกราฟสนามลูกศรบนคอนทัวร์ของกราฟ sin เหมือนอย่างในบทที่แล้วกันดู
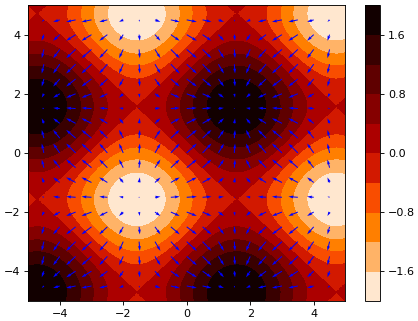
จะเห็นว่าได้กราฟออกมาใกล้เคียงจากรูปเดิมในบทที่แล้ว (ลองย้อนกลับไปดูเทียบกัน) ต่างกันที่กำหนดสีไว้เป็นคนละสีเท่านั้น
เราสามารถใช้วิธีนี้เพื่อหาค่าความชันของค่าอะไรต่างๆอย่างง่ายได้ สามารถใช้เพื่อทำแผนภาพลูกศรบนคอนทัวร์แบบนี้ได้
อ้างอิง
การหาค่าความเปลี่ยนแปลงของสมาชิกแต่ละตัวในอาเรย์ด้วย np.diff
การหาอนุพันธ์เชิงตัวเลขอย่างง่ายสุดก็คือการคำนวณค่าความเปลี่ยนแปลงระหว่างสมาชิกแต่ละตัวในอาเรย์
ถ้าลองทำโดยใช้ for ก็จะเป็น
import numpy as np
y = np.arange(8.)*10
print(y) # ได้ [ 0. 10. 20. 30. 40. 50. 60. 70.]
dy = np.empty(len(y)-1)
for i in range(len(y)-1):
dy[i] = y[i+1]-y[i]
print(dy) # ได้ [ 10. 10. 10. 10. 10. 10. 10.]
y = np.arange(8.)*10
print(y) # ได้ [ 0. 10. 20. 30. 40. 50. 60. 70.]
dy = np.empty(len(y)-1)
for i in range(len(y)-1):
dy[i] = y[i+1]-y[i]
print(dy) # ได้ [ 10. 10. 10. 10. 10. 10. 10.]
แต่เราสามารถทำได้ง่ายกว่านั้นด้วยการอาเรย์ตัวนี้ที่ตัดส่วนหัวกับที่ตัดส่วนท้ายมาลบกัน นั่นคือ y[1:]-y[:-1]
print(y[1:]-y[:-1]) # ได้ [ 10. 10. 10. 10. 10. 10. 10.]
แต่มีฟังก์ชันที่ไว้ใช้เพื่อการนั้นโดยเฉพาะ นั่นคือ np.diff
print(np.diff(y)) # ได้ [ 10. 10. 10. 10. 10. 10. 10.]
หากต้องการอาอนุพันธ์อันดับสองขึ้นไปก็ทำได้โดยการใส่อาร์กิวเมนต์ตัวที่สองลงไป
print(np.diff(y,2)) # ได้ [ 0. 0. 0. 0. 0. 0.]
อันนี้เป็นเพราะว่าอนุพันธ์อันดับหนึ่งเท่ากันหมด ดังนั้นอันดับสองจึงเป็น 0
หากลองใหม่เป็นค่าที่มาจากฟังก์ชันยกกำลังสองจะได้อาเรย์ที่มีค่าไม่เป็น 0 ไปจนถึงอันดับที่สอง
y = np.arange(8.)**2
print(y) # ได้ [ 0. 1. 4. 9. 16. 25. 36. 49.]
print(np.diff(y)) # ได้ [ 1. 3. 5. 7. 9. 11. 13.]
print(np.diff(y,2)) # ได้ [ 2. 2. 2. 2. 2. 2.]
print(np.diff(y,3)) # ได้ [ 0. 0. 0. 0. 0.]
print(y) # ได้ [ 0. 1. 4. 9. 16. 25. 36. 49.]
print(np.diff(y)) # ได้ [ 1. 3. 5. 7. 9. 11. 13.]
print(np.diff(y,2)) # ได้ [ 2. 2. 2. 2. 2. 2.]
print(np.diff(y,3)) # ได้ [ 0. 0. 0. 0. 0.]
ฟังก์ชันนี้ตรงกันข้ามกันกับ np.cumsum ซึ่งเคยกล่าวถึงไปแล้วในบทที่ ๑๗ ดังนั้นหากใช้ฟังก์ชันนี้กับฟังก์ชันที่ได้จาก np.cumsum ก็จะได้ผลใกล้เคียงอาเรย์เดิม
ตัวอย่าง
y = np.arange(3,13)**2
print(y) # ได้ [ 9 16 25 36 49 64 81 100 121 144]
print(np.cumsum(y)) # ได้ [ 9 25 50 86 135 199 280 380 501 645]
print(np.diff(np.cumsum(y))) # ได้ [ 16 25 36 49 64 81 100 121 144]
print(np.cumsum(np.diff(y))) # ได้ [ 7 16 27 40 55 72 91 112 135]
print(y) # ได้ [ 9 16 25 36 49 64 81 100 121 144]
print(np.cumsum(y)) # ได้ [ 9 25 50 86 135 199 280 380 501 645]
print(np.diff(np.cumsum(y))) # ได้ [ 16 25 36 49 64 81 100 121 144]
print(np.cumsum(np.diff(y))) # ได้ [ 7 16 27 40 55 72 91 112 135]
จะเห็นว่าผลที่ได้จากการ np.cumsum แล้ว np.diff หรือ np.diff แล้วค่อย np.cumsum จะออกมาคล้ายตัวเดิมแต่มีสมาชิกหายไปตัวหนึ่ง
นั่นเพราะว่าเวลาใช้ np.diff แล้วจำนวนสมาชิกจะลดลงไปตัวหนึ่งเสมอ นั่นก็เป็นข้อเสียของฟังก์ชันนี้
และสิ่งที่ np.diff คำนวณได้นั้นคือความต่างของค่าของสมาชิกทีละตัว ในกรณีที่สมาชิกในแต่ละตัวนั้นแทนค่าของฟังก์ชัน f(x) ที่ x = 1,2,3 ตามลำดับไปเรื่อยๆค่าที่ได้จาก np.diff ก็จะเป็นค่าอนุพันธ์โดยประมาณทันที แต่โดยทั่วไประยะห่างระหว่างค่า x แต่ละค่าอาจเป็นจำนวนใดๆซึ่งยิ่งเล็กก็ยิ่งดี
การคำนวณของ np.diff นั้นเป็นการหาอนุพันธ์ในรูปแบบของสูตรผลต่างแบบไปข้างหน้าที่มีความแม่น อันดับหนึ่ง ซึ่งหากเขียนเป็นสมการก็จะได้ว่า
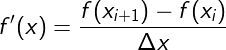
แต่อย่างที่เห็นก็คือ np.diff แค่เอาค่าในลำดับต่อกันมาลบกันเฉยๆ ไม่ได้หาร Δx ดังนั้นหากเรารู้ค่า Δx จริงๆว่าเป็นเท่าไหร่ก็เอาค่านั้นไปหารจึงจะได้ค่าอนุพันธ์ที่แท้จริง
อย่างไรก็ตาม สำหรับการคำนวณหาอนุพันธ์ที่ดีกว่านั้นเราอาจควรเลือกใช้ฟังก์ชันอีกตัวหนึ่ง นั่นคือ np.gradient
การหาอนุพันธ์ด้วย np.gradient
np.gradient เป็นฟังก์ชันสำหรับหาอนุพันธ์เชิงตัวเลขของอาเรย์โดยใช้สูตรผลต่างแบบตรงกลางที่มีความแม่นอันดับสอง นั่นคือ
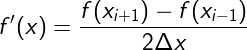
ซึ่งจะมีความแม่นยำมากกว่า np.diff ซึ่งใช้สูตรผลต่างแบบไปข้างหน้าที่มีความแม่นอันดับหนึ่ง เพราะว่านำทั้งตัวหน้าและตัวหลังมาคิด
เพียงแต่ว่าค่าตัวแรกสุดจะไม่มีค่าก่อนหน้ามัน (i-1) ดังนั้นจึงได้แต่ใช้สูตรผลต่างแบบไปข้างหน้าที่มีความแม่นอันดับหนึ่งเช่น เดียวกับ np.diff ดังนั้นตัวแรกของ np.diff และ np.gradient ควรจะได้ค่าเหมือนกัน
ส่วนค่าตัวสุดท้ายจะไม่มีตัวที่อยู่หลังมัน (i+1) ดังนั้นจึงต้องใช้สูตรผลต่างแบบย้อนกลับที่มีความแม่นอันดับหนึ่ง นั่นคือ
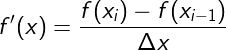
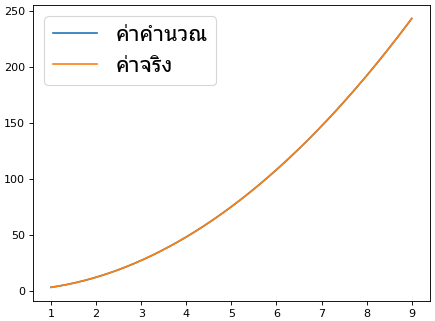
ตัวอย่างการใช้ ลองหาอนุพันธ์ของ x กำลัง 3 ด้วยวิธีนี้แล้วเทียบกับกราฟอนุพันธ์จริงๆซึ่งควรเป็น 3x**2
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(1,9,1.)
y = x**3
dify = np.gradient(y)
print(y) # ได้ [ 1. 8. 27. 64. 125. 216. 343. 512.]
print(dify) # ได้ [ 7. 13. 28. 49. 76. 109. 148. 169.]
print(3*x**2) # ได้ [ 3. 12. 27. 48. 75. 108. 147. 192.]
plt.plot(x,dify,label=u'ค่าคำนวณ')
plt.plot(x,3*x**2,label=u'ค่าจริง')
plt.legend(prop={'family':'Tahoma','size':20})
plt.show()
import matplotlib.pyplot as plt
x = np.arange(1,9,1.)
y = x**3
dify = np.gradient(y)
print(y) # ได้ [ 1. 8. 27. 64. 125. 216. 343. 512.]
print(dify) # ได้ [ 7. 13. 28. 49. 76. 109. 148. 169.]
print(3*x**2) # ได้ [ 3. 12. 27. 48. 75. 108. 147. 192.]
plt.plot(x,dify,label=u'ค่าคำนวณ')
plt.plot(x,3*x**2,label=u'ค่าจริง')
plt.legend(prop={'family':'Tahoma','size':20})
plt.show()

เห็นได้ชัดว่ามีความคลาดเคลื่อน ซึ่งยังไงก็หลีกเลี่ยงไม่ได้ โดยเฉพาะที่ปลาย
เพื่อความแม่นยำมากขึ้นเราสามารถกำหนดให้ที่ปลายทั้งสองข้างใช้การหาอนุพันธ์โดย สูตรผลต่างที่มีความแม่นยำอันดับสองได้โดยเพิ่มคีย์เวิร์ด edge_order=2
แบบนี้แล้วที่ตัวแรกจะเป็นการคำนวณโดยใช้สูตรผลต่างแบบไปข้างหน้าที่มีความแม่น อันดับสอง นั่นคือนอกจากจะเอาค่าที่ตำแหน่งนั้น (i) และตำแหน่งถัดไป (i+1) แล้วยังนำตำแหน่งถัดจากนั้นไปอีก (i+2) มาคิดด้วย
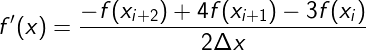
สัมประสิทธิ์ที่เป็น 4 และ 3 ที่เห็นด้านหน้านี้มาจากการคิดโดยอนุกรมเทย์เลอร์
ส่วนตัวสุดท้ายจะกลับกัน คือเอาที่ตำแหน่งนั้น (i) และตำแหน่งก่อนหน้านั้น (i-1) และก่อนหน้านั้นไปอีก (i-2)
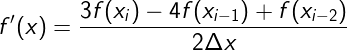
ลองทำดูใหม่โดยใส่ edge_order=2 จะได้เป็น
print(np.gradient(y,edge_order=2)) # [ 1. 13. 28. 49. 76. 109. 148. 190.]
จะเห็นได้ว่าค่าที่ขอบปลายทั้งสองข้างเปลี่ยนไปโดยใกล้เคียงกว่าเดิม แม้จะยังคงมีความคลาดเคลื่อนอยู่
การคำนวณเชิงตัวเลขนั้นยังไงความคลาดเคลื่อนก็เป็นสิ่งที่หลีกเลี่ยงไม่ได้อยู่ แล้ว แต่ว่ายิ่งค่าที่ใช้คำนวณมีความละเอียดเท่าไหร่ความคลาดเคลื่อนก็จะยิ่งน้อย ลงเท่านั้น ในการใช้งานจริงๆมักจะใช้ค่า Δx เล็กมากๆเพื่อให้ความคลาดเคลื่อนต่ำจนอยู่ในระดับที่ยอมรับได้
ในตัวอย่างข้างต้นนี้เราไม่ได้กำหนดค่า Δx ดังนั้นจึงถือว่า Δx เป็น 1 ไปโดยปริยาย แต่เราสามารถกำหนดค่า Δx ได้โดยใส่ลงไปเป็นอาร์กิวเมนต์ตัวที่สอง
ลองทำกับฟังก์ชันเดิม แต่เพิ่มความละเอียดโดย Δx เป็น 0.01
dx = 0.01 # Δx
x = np.arange(1,9.01,dx)
y = x**3
dify = np.gradient(y,dx,edge_order=2)
print(dify-3*x**2) # ได้อาเรย์ที่แต่ละตัวมีค่าน้อยมาก
print(np.mean(dify-3*x**2)) # ค่าความต่างเฉลี่ย ได้ 9.92509363979e-05
plt.plot(x,dify,label=u'ค่าคำนวณ')
plt.plot(x,3*x**2,label=u'ค่าจริง')
plt.legend(prop={'family':'Tahoma','size':20})
plt.show()
x = np.arange(1,9.01,dx)
y = x**3
dify = np.gradient(y,dx,edge_order=2)
print(dify-3*x**2) # ได้อาเรย์ที่แต่ละตัวมีค่าน้อยมาก
print(np.mean(dify-3*x**2)) # ค่าความต่างเฉลี่ย ได้ 9.92509363979e-05
plt.plot(x,dify,label=u'ค่าคำนวณ')
plt.plot(x,3*x**2,label=u'ค่าจริง')
plt.legend(prop={'family':'Tahoma','size':20})
plt.show()

อนุพันธ์ย่อย
ในตัวอย่างที่ผ่านๆมาเราใช้ np.gradient และ np.diff กับอาเรย์หนึ่งมิติ แต่ที่จริงแล้วทั้งสองฟังก์ชันนี้จะใช้กับอาเรย์กี่มิติก็ได้
หากใช้กับอาเรย์สองมิติขึ้นไป สิ่งที่หาได้ก็จะเป็นอนุพันธ์ย่อย นั่นคืออนุพันธ์ของค่า f(x,y) เมื่อเทียบกับ x หรือ y แยกกัน
ค่าคืนกลับที่ได้จาก np.gradient ในกรณีสองมิติจะออกมาเป็นลิสต์ที่มีสมาชิกอยู่สองตัว คือค่าอนุพันธ์ย่อยในแกน y และ x
ตัวอย่างเช่น พิจารณาฟังก์ชัน z = x**2 + y**2 - 9 ซึ่งหากคำนวณก็จะได้ผลออกมาตามนี้
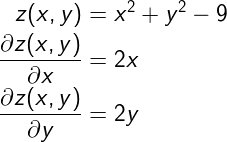
คราวนี้มาลองหาโดยใช้ np.gradient ดู
x,y = np.meshgrid(np.arange(-3,4,1.),np.arange(-3,4,1.))
z = x**2 + y**2 - 9
dzy,dzx = np.gradient(z,edge_order=2)
print(z)
print(dzx)
print(dzy)
z = x**2 + y**2 - 9
dzy,dzx = np.gradient(z,edge_order=2)
print(z)
print(dzx)
print(dzy)
ได้
[[ 9. 4. 1. 0. 1. 4. 9.]
[ 4. -1. -4. -5. -4. -1. 4.]
[ 1. -4. -7. -8. -7. -4. 1.]
[ 0. -5. -8. -9. -8. -5. 0.]
[ 1. -4. -7. -8. -7. -4. 1.]
[ 4. -1. -4. -5. -4. -1. 4.]
[ 9. 4. 1. 0. 1. 4. 9.]]
[[-6. -6. -6. -6. -6. -6. -6.]
[-4. -4. -4. -4. -4. -4. -4.]
[-2. -2. -2. -2. -2. -2. -2.]
[ 0. 0. 0. 0. 0. 0. 0.]
[ 2. 2. 2. 2. 2. 2. 2.]
[ 4. 4. 4. 4. 4. 4. 4.]
[ 6. 6. 6. 6. 6. 6. 6.]]
[[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]]
[ 4. -1. -4. -5. -4. -1. 4.]
[ 1. -4. -7. -8. -7. -4. 1.]
[ 0. -5. -8. -9. -8. -5. 0.]
[ 1. -4. -7. -8. -7. -4. 1.]
[ 4. -1. -4. -5. -4. -1. 4.]
[ 9. 4. 1. 0. 1. 4. 9.]]
[[-6. -6. -6. -6. -6. -6. -6.]
[-4. -4. -4. -4. -4. -4. -4.]
[-2. -2. -2. -2. -2. -2. -2.]
[ 0. 0. 0. 0. 0. 0. 0.]
[ 2. 2. 2. 2. 2. 2. 2.]
[ 4. 4. 4. 4. 4. 4. 4.]
[ 6. 6. 6. 6. 6. 6. 6.]]
[[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]
[-6. -4. -2. 0. 2. 4. 6.]]
กรณีที่จะระบุค่า Δx และ Δy ก็ให้ใส่เป็นอาร์กิวเมนต์ต่อกันไป
x,y = np.meshgrid(np.arange(-3,3.01,0.01),np.arange(-3,3.01,0.01))
z = x**2 + y**2 - 9
dzy,dzx = np.gradient(z,0.01,0.01,edge_order=2)
z = x**2 + y**2 - 9
dzy,dzx = np.gradient(z,0.01,0.01,edge_order=2)
ลองนำมาวาดเป็นกราฟสนามลูกศรบนคอนทัวร์ของกราฟ sin เหมือนอย่างในบทที่แล้วกันดู
x,y = np.meshgrid(np.linspace(-5,5,101),np.linspace(-5,5,101))
z = np.sin(x)+np.sin(y) # ค่า z ซึ่งจะใช้เป็นสีในคอนทัวร์
plt.contourf(x,y,z,12,cmap='gist_heat_r')
plt.colorbar()
dzy,dzx = np.gradient(z,0.1,0.1,edge_order=2) # หาค่าความชัน
qx = x[5:96:5,5:96:5]
qy = y[5:96:5,5:96:5]
u = dzx[5:96:5,5:96:5] # ค่า u และ v ของลูกศรมาจากความชันของ z ในแกน x และ y ที่หาได้โดยลดความถี่ในการแสดงผล
v = dzy[5:96:5,5:96:5]
plt.quiver(qx,qy,u,v,color='b',angles='xy',scale_units='xy')
plt.show()
z = np.sin(x)+np.sin(y) # ค่า z ซึ่งจะใช้เป็นสีในคอนทัวร์
plt.contourf(x,y,z,12,cmap='gist_heat_r')
plt.colorbar()
dzy,dzx = np.gradient(z,0.1,0.1,edge_order=2) # หาค่าความชัน
qx = x[5:96:5,5:96:5]
qy = y[5:96:5,5:96:5]
u = dzx[5:96:5,5:96:5] # ค่า u และ v ของลูกศรมาจากความชันของ z ในแกน x และ y ที่หาได้โดยลดความถี่ในการแสดงผล
v = dzy[5:96:5,5:96:5]
plt.quiver(qx,qy,u,v,color='b',angles='xy',scale_units='xy')
plt.show()

จะเห็นว่าได้กราฟออกมาใกล้เคียงจากรูปเดิมในบทที่แล้ว (ลองย้อนกลับไปดูเทียบกัน) ต่างกันที่กำหนดสีไว้เป็นคนละสีเท่านั้น
เราสามารถใช้วิธีนี้เพื่อหาค่าความชันของค่าอะไรต่างๆอย่างง่ายได้ สามารถใช้เพื่อทำแผนภาพลูกศรบนคอนทัวร์แบบนี้ได้
อ้างอิง