ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๑๒: การแจกแจงแบบปกติและทฤษฎีขีดจำกัดกลาง
เขียนเมื่อ 2020/08/01 14:44
แก้ไขล่าสุด 2021/09/28 16:42
ต่อจาก บทที่ ๑๑
บทนี้ว่าด้วยเรื่องของการแจกแจงแบบปกติ ซึ่งเป็นการแจกแจงที่ใช้แพร่หลายที่สุด รวมถึงทฤษฎีขีดจำกัดกลางซึ่งมีคามเกี่ยวข้องกัน
ทฤษฎีขีดจำกัดกลาง
การแจกแจงแบบปกติ (正态分布, normal distribution) หรือเรียกอีกอย่างว่า การแจกแจงแบบเกาส์ (高斯分布, Gaussian distribution) เป็นการแจกแจงที่พบได้ทั่วไปที่สุดในธรรมชาติ กล่าวคือปรากฏการณ์ใดๆที่มีการสุ่ม ถ้าปล่อยให้สุ่มไปโดยอิสระมักจะเกิดการแจกแจงความน่าจะเป็นแบบปกติขึ้นได้ง่ายที่สุด
หลักการที่อธิบายเรื่องนี้เรียกว่า ทฤษฎีขีดจำกัดกลาง (中心极限定理, central limit theorem)
ในทฤษฎีขีดจำกัดกลางได้บอกไว้ว่าถ้าหาค่าเฉลี่ยของตัวแปรสุ่มใดๆที่มีการลองทำซ้ำเป็นจำนวนมากๆ การแจกแจงความน่าจะเป็นของค่าเฉลี่ยที่จะได้นี้จะเป็นการแจกแจงแบบปกติ ไม่ว่าตัวแปรสุ่มนั้นเดิมทีจะมีการแจกแจงแบบใดก็ตาม
เพื่อให้เห็นภาพ ขอเริ่มจากยกตัวอย่างโดยใช้การแจกแจงแบบคงที่ โดยให้ค่าออกมาเป็น 1 ถึง 999 โดยที่แต่ละค่ามีความน่าจะเป็นเท่ากันหมด
ก่อนอื่นลองเขียนโปรแกรมไพธอนให้สุ่มมาสักแสนตัว (ขอเยอะหน่อยเพื่อให้รูปร่างการแจกแจงค่อนข้างแน่นอน) แล้ววาดฮิสโทแกรมขึ้นมาดูการแจกแจง
import random
import matplotlib.pyplot as plt
x = []
for i in range(100000):
x += [random.randint(1,999)]
plt.hist(x,50,ec='k')
plt.show()จะได้การแจกแจงในแต่ละช่วงค่อนข้างสม่ำเสมอกัน
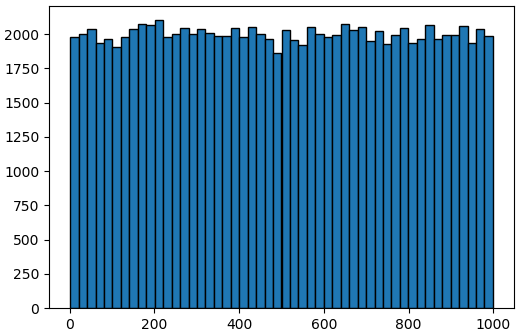
จากนั้นมาดูว่าจะเกิดอะไรขึ้นถ้าหากเราเปลี่ยนเป็นทำการสุ่มทั้งหมด 100 ครั้งแล้วเอาค่าที่ได้มาเฉลี่ยกัน
ลองแสดงการแจกแจงโดยลองทำแสนครั้งเช่นเดิม แต่คราวนี้เป็นค่าเฉลี่ยจากการบวกกัน 100 ครั้ง
import random
import matplotlib.pyplot as plt
n = 100
x = []
for i in range(100000):
ruam = 0
for j in range(n):
ruam += random.randint(1,999)
x += [ruam/n]
plt.hist(x,50,color='#ffc0f2',ec='k')
plt.show()ผลที่ได้จะไม่ใช่ลักษณะการแจกแจงที่คงตัวอีกแล้ว แต่กลายเป็นทรงระฆังคว่ำแบบนี้เอง นี่ก็คือการแจกแจงแบบที่เรียกว่าการแจกแจงแบบปกติ
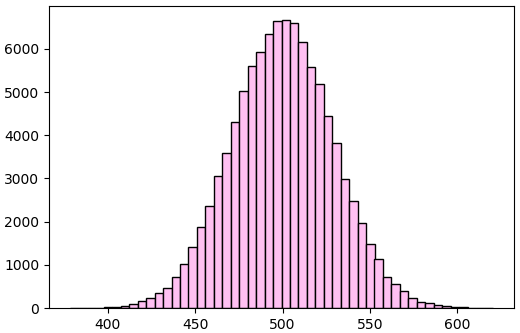
นี่คือสิ่งที่จะเกิดขึ้นเมื่อหาค่าเฉลี่ยจากการสุ่มของตัวแปรสุ่มใดๆหลายตัวมากพอ ในที่นี้คือ 100 ซึ่งถือว่าเยอะพอที่จะเห็นผลได้
ลักษณะการการแจกแจงจะยิ่งใกล้เคียงการแจกแจงแบบปกติเมื่อการจำนวนที่สุ่มเยอะขึ้น
ลองทำแบบเดิมแต่เทียบที่จำนวนครั้งที่สุ่มดู คำนวณค่าเฉลี่ยระหว่างการสุ่ม n ครั้ง ตั้งแต่ n=1 ไปจนถึง 128
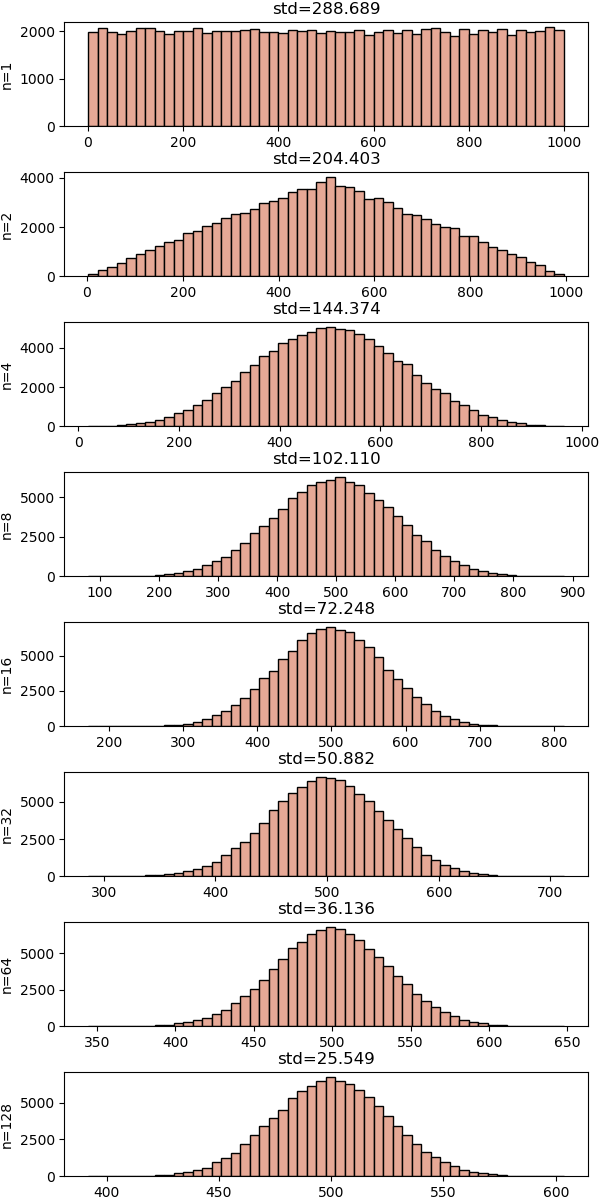
จะเห็นว่าถ้าทำแค่ครั้งเดียวก็ยังเป็นการแจกแจงแบบเท่ากันตามปกติ แต่พอเป็น 2 ครั้งรูปร่างก็เริ่มเปลี่ยนไป และยิ่งเพิ่มจำนวนครั้งมากขึ้นการแจกแจงก็ค่อยๆเปลี่ยนไป กลายเป็นเหมือสระฆังคว่ำ
และในภาพนี้ได้แสดงค่าส่วนเบี่ยงเบนมาตรฐาน (std) ไว้ด้วย ซึ่งจะเห็นว่าเมื่อเพิ่มจำนวนครั้ง 4 เท่าจะมีส่วนเบี่ยงเบนมาตรฐานลดลงเหลือครึ่งหนึ่ง
การลดลงของส่วนเบี่ยงเบนมาตรฐานในการแจกแจงได้อธิบายไว้แล้วในกฎว่าด้วยจำนวนมาก ซึ่งเขียนไว้ในบทที่ ๔ ซึ่งบอกว่าตัวแปรสุ่มใดๆก็ตาม ถ้าสุ่มหลายๆครั้งมากเข้าแล้วหาค่าเฉลี่ยก็จะได้ค่าเข้าใกล้ค่าคาดหมายของการแจกแจงนั้น และความแปรปรวนก็จะเท่ากับความแปรปรวนของการแจกแจงนั้นหารด้วยจำนวนครั้งที่ลอง
ยิ่งเพิ่มจำนวนมากขึ้น รูปร่างของการแจกแจงจะเริ่มคงตัวเป็นระฆังคว่ำตามการแจกแจงแบบปกติไม่มีเปลี่ยนแปลง แต่ความกว้างในการแจกแจงก็จะยังคงบีบแคบลงเรื่องๆ โดยเป็นสัดส่วนตามรากที่สองของจำนวนครั้ง
ลักษณะการแจกแจงที่เปลี่ยนไปเป็นทรงระฆังคว่ำแบบนี้ยังเกิดขึ้นกับการแจกแจงแบบอื่นด้วย คือไม่ว่าเดิมจะมีการแจกแจงอย่างไร พอนำการแจกแจงนั้นมาเฉลี่ยกันหลายครั้งเข้าก็จะกลายเป็นการแจกแจงแบบปกติ
ขอยกตัวอย่างให้ดูอีก ๒ ตัวอย่าง คือการแจกแจงแบบเอกรูปต่อเนื่องและแบบเรขาคณิต
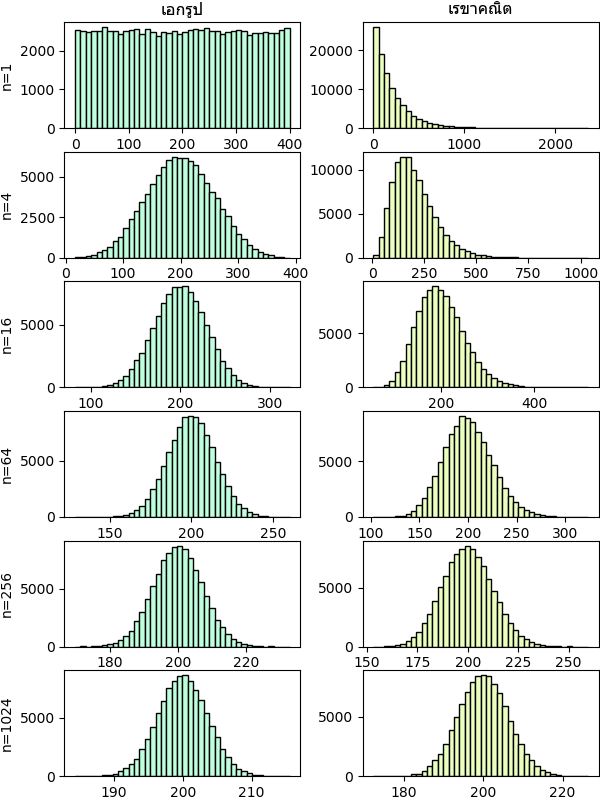
ด้านซ้ายคือการแจกแจงเอกรูปต่อเนื่อง (ดูบทที่ ๘) โดยให้แจกแจงด้วยค่าคงที่ตั้งแต่ 0 ถึง 400
ส่วนด้านขวาเป็นการแจกแจงแบบเรขาคณิต (ดูบทที่ ๖) โดยที่ p=0.005
จะเห็นว่าแม้แต่การแจกแจงแบบเรขาคณิตซึ่งเดิมทีจะมีค่ามากสุดที่ 1 ก็เริ่มค่อยๆเปลี่ยนไปกลายเป็นทรงระฆังคว่ำเมื่อหาค่าเฉลี่ยจากการทำซ้ำหลายๆครั้งมากเข้า แม้ว่าจะเปลี่ยนช้ากว่าการแจกแจงเอกรูปก็ตาม
นอกจากนี้ความกว้างของระฆัง (ส่วนเบี่ยงเบนมาตรฐาน) ก็ลดลงเรื่อยๆตามกฎว่าด้วยจำนวนมาก
ฟังก์ชันเกาส์กับการแจกแจงแบบปกติ
เมื่ออธิบายตัวอย่างที่ทำให้เกิดการแจกแจงแบบปกติและได้แสดงให้เห็นถึงความสำคัญของการแจกแจงแบบนี้ไปแล้ว คราวนี้มาดูว่าถ้าเขียนเป็นสูตรจะได้เป็นอย่างไร
การแจกแจงแบบปกตินั้นบางทีก็เรียกว่าการแจกแจงแบบเกาส์ เพราะมีลักษณะเป็นฟังก์ชันเกาส์ นั่นคือ
โดย σ คือส่วนเบี่ยงเบนมาตรฐานของการแจกแจง ส่วน μ คือจุดกึ่งกลางของการแจกแจง
แต่ในการแจกแจงความน่าจะเป็นนั้นจะต้องทำให้ผลรวมของการแจกแจงทั้งหมดเป็น 1 ดังนั้นจึงหารด้วยพื้นที่รวมทั้งหมด
โดยที่พื้นที่ใต้กราฟได้จากการหาปริพันธ์ตั้งแต่ลบอนันต์ถึงอนันต์ ซึ่งได้เป็น
(สำหรับวิธีคำนวณปริพันธ์ ขอละไว้)
ดังนั้นการแจกแจงความน่าจะเป็นแบบปกติจึงเป็น
โดยค่าคาดหวังของการแจกแจงแบบนี้จะมีค่าเป็น μ และความแปรปรวนจะมีค่าเป็น σ2
กรณีที่ μ=0 และ σ=1 นั่นหมายถึงใจกลางอยู่ที่ 0 และส่วนเบี่ยงเบนมาตรฐานเป็น 1 จะเรียกว่าเป็นการแจกแจงแบบปกติมาตรฐาน (标准正态分布, standard normal distribution)
ลองวาดกราฟเปรียบเทียบการแจกแจงแบบปกติที่ค่า σ ต่างๆกันไป โดยที่ μ เป็น 0
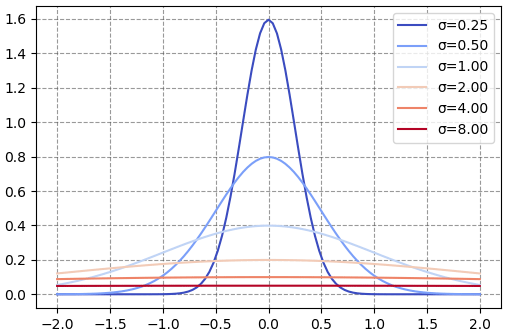
จะเห็นว่ายิ่ง σ มากก็ยิ่งมีการแจกแจงกระจายไปเป็นบริเวณกว้าง ถ้า σ จะกองอยู่ตรงกลางเยอะ
หากนำการแจกแจงแบบปกติมาวาดดูการแจกแจงความน่าจะเป็นสะสมก็จะได้เป็นแบบนี้
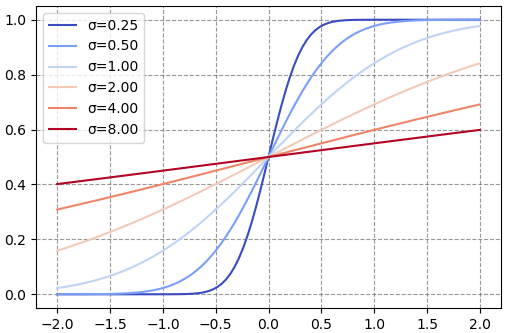
ในมอดูล random มีฟังก์ชัน gauss() ไว้สุ่มโดยมีการแจกแจงแบบปกติ
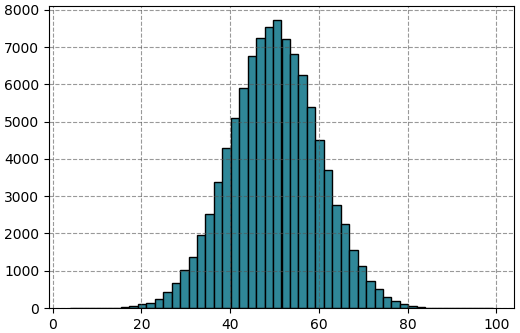
ตัวอย่าง ลองสุ่มการแจกแจงแบบปกติโดยให้มี μ=50 และ σ=10 สักแสนตัวแล้ววาดฮิสโทแกรม
import random
import matplotlib.pyplot as plt
x = []
for i in range(100000):
x += [random.gauss(50,10)]
plt.hist(x,50,color='#2f8798',ec='k')
plt.grid(ls='--',color='#555555',alpha=0.6)
plt.show()ได้การแจกแจงดังนี้
ความน่าเป็นสะสมรวมจากใจกลาง
ลักษณะของการแจกแจงแบบปกตินั้นที่ตำแหน่งใจกลาง (μ) มีค่าสูงสุด และลดลงเรื่อยๆอย่างรวดเร็วเมื่อห่างจากใจกลาง
ดังนั้นความน่าจะเป็นส่วนใหญ่จะอัดกันแน่นอยู่ที่ใกล้ๆใจกลาง โดยขึ้นอยู่กับจำนวนเท่าของ σ เช่นในช่วงห่างจากใจกลางไม่เกิน 1σ ความน่าจะเป็นจะมีค่าสูงถึง 68.3% ถ้าห่างภายใน 2σ ก็เป็น 95.4% และถ้าห่างภายใน 3σ ก็ครอบคลุมถึง 99.7% แล้ว
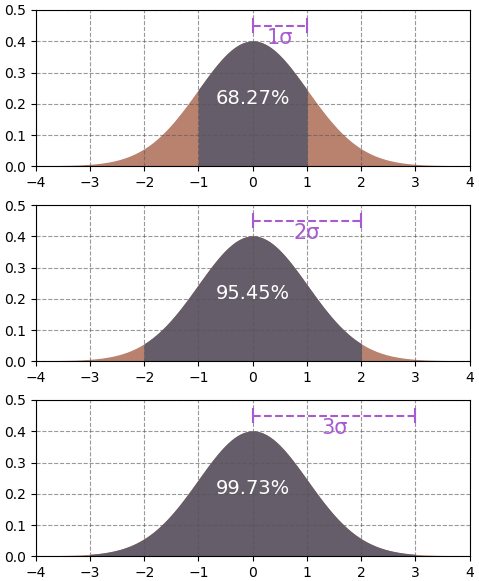
ตารางเทียบระหว่างระยะห่างจากใจกลางกับความน่าจะเป็นรวมภายในระยะนั้น
| ระยะห่าง ± จาก μ | ร้อยละของพื้นที่ใต้กราฟ |
|---|---|
| 0.318 639σ | 25% |
| 0.674490σ | 50% |
| 0.994458σ | 68% |
| 1σ | ≈68.2689492% |
| 1.281552σ | 80% |
| 1.644854σ | 90% |
| 1.959964σ | 95% |
| 2σ | ≈95.4499736% |
| 2.575829σ | 99% |
| 3σ | ≈99.7300204% |
| 3.290527σ | 99.9% |
| 3.890592σ | 99.99% |
| 4σ | ≈99.993666% |
| 4.417173σ | 99.999% |
| 4.891638σ | 99.9999% |
| 5σ | ≈99.9999426697% |
| 5.326724σ | 99.99999% |
| 5.730729σ | 99.999999% |
| 6σ | ≈99.9999998027% |
| 6.109410σ | 99.9999999% |
| 6.466951σ | 99.99999999% |
| 6.806502σ | 99.999999999% |
| 7σ | ≈99.9999999997440% |
เวลาวัดค่าอะไรก็ตามในธรรมชาติแม้ว่าค่านั้นอาจจะไม่ได้แจกแจงแบบปกติเสมอไป แต่โดยทั่วไปมักจะถือว่ามีการแจกแจงเป็นแบบปกติได้
ดังนั้นค่าตรงนี้จึงมักถูกนำไปใช้ในทางสถิติ เพื่อจะสรุปว่าค่าที่วัดได้มีความคลาดเคลื่อนในระดับที่ยอมรับได้หรือไม่ โดยดูว่าในระยะห่างจากใจกลางเท่านั้นมีค่าเป็นกี่เท่าของ σ แล้วดูว่าที่ภายในระยะเท่านั้นครอบคลุมความน่าจะเป็นมากแค่ไหน
เช่นโดยทั่วไปแล้วอาจมองได้ว่าถ้าห่างเกิน 3σ ก็จะถือว่าแทบเป็นไปได้แล้ว เพราะความน่าจะเป็นที่จะออกนอกขอบเขตไปไกลขนาดนั้นจะเหลือเพียง 0.27% เท่านั้น
ลองเขียนโค้ดทำการลองสุ่มดูสักแสนตัวแล้วหาว่ามีกี่ตัวที่อยู่ภายในระยะที่กำหนดเป็นสัดส่วนเท่าไหร่
import random
n = 100000 # จำนวนทั้งหมด
sigma1 = 0 # จำนวนที่อยู๋ใน 1σ
sigma2 = 0 # จำนวนที่อยู๋ใน 2σ
sigma3 = 0 # จำนวนที่อยู๋ใน 3σ
for i in range(n):
x = random.gauss(0,1)
if(-1<=x<=1):
sigma1 += 1
if(-2<=x<=2):
sigma2 += 1
if(-3<=x<=3):
sigma3 += 1
print(sigma1/n) # ได้ 0.68267
print(sigma2/n) # ได้ 0.95426
print(sigma3/n) # ได้ 0.99761จำนวนที่ได้ออกมาใกล้เคียงสอดคล้องกับค่าในตารางข้างบนที่ 1σ,2σ,3σ
เทียบการแจกแจงแบบปกติกับการแจกแจงทวินาม
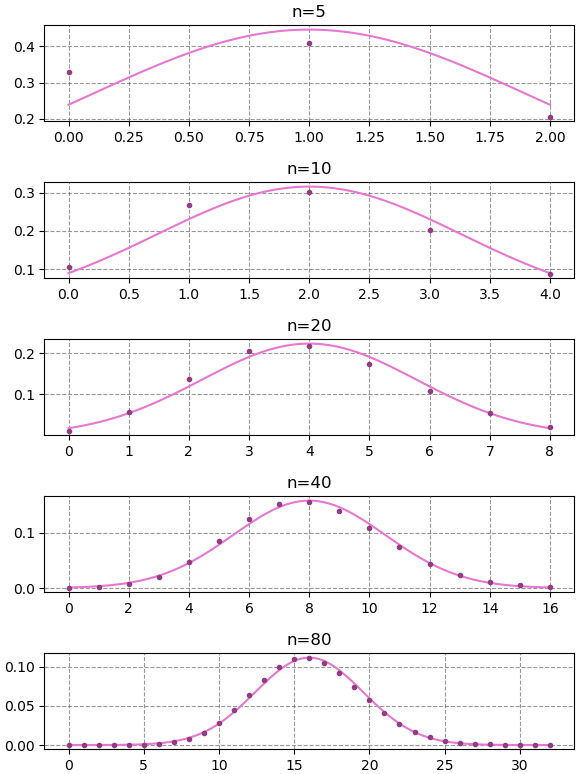
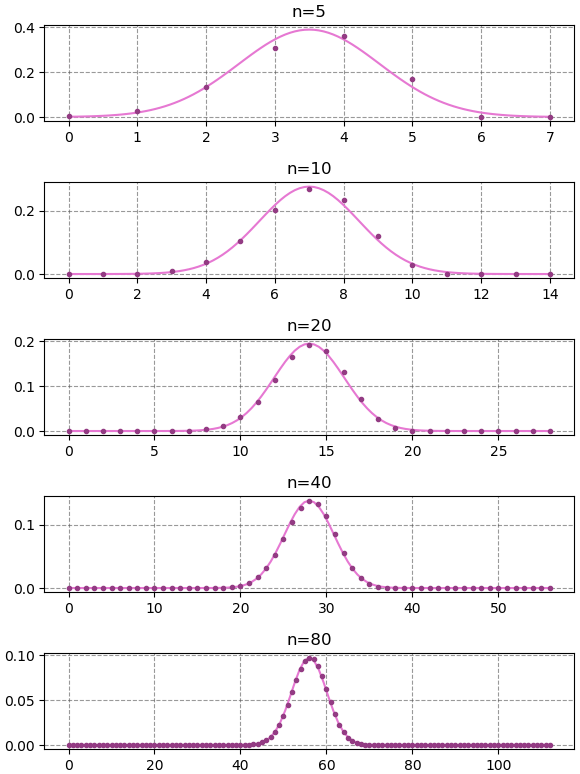
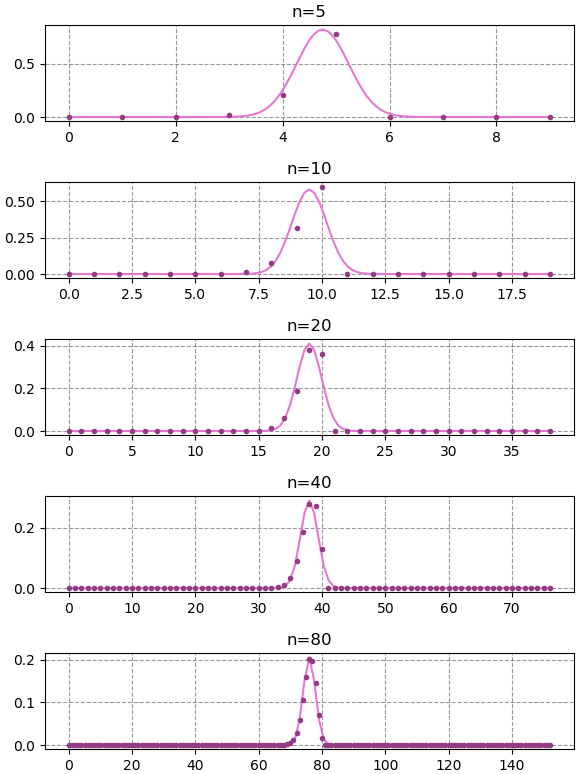
การแจกแจงทวินาม (ดูบทที่ ๕) นั้นกรณีที่ n (จำนวนครั้งที่ลอง) มีค่ามากพอ และ p (ความน่าจะเป็นที่จะสำเร็จ) ไม่ใกล้ 0 หรือ 1 มากเกินไป จะมีรูปร่างคล้ายระฆังคว่ำ และสามารถประมาณเป็นการแจกแจงแบบปกติซึ่ง μ=np และ σ2=np(1-p)
ลองวาดกราฟค่าของการแจกแจงทวินาม (แทนด้วยจุด) เทียบกับการแจกแจงแบบปกติ (แทนด้วยเส้น)
กรณี p = 0.2 เมื่อ n สูงๆมากเข้าก็จะเห็นว่าเริ่มประมาณได้ใกล้เคียงกัน
กรณี p = 0.7 จะประมาณออกมาได้ใกล้เคียงกว่า
กรณี p = 0.95 เนื่องจากว่า p เข้าใกล้ 1 จึงประมาณออกมาได้ไม่ใกล้เคียงนักแม้เมื่อ n เยอะ
เทียบการแจกแจงแบบปกติกับการแจกแจงปัวซง
การแจกแจงปัวซง (ดูบทที่ ๗) นั้นในกรณีที่ λ มีค่ามากพอ จะสามารถประมาณเป็นการแจกแจงแบบปกติได้ โดย μ=λ, σ2=λ
ลองวาดกราฟเปรียบเทียบค่าของการแจกแจงปัวซง (จุด) และการแจกแจงแบบปกติ (เส้น) ในกรณี λ เป็นค่าต่างๆ
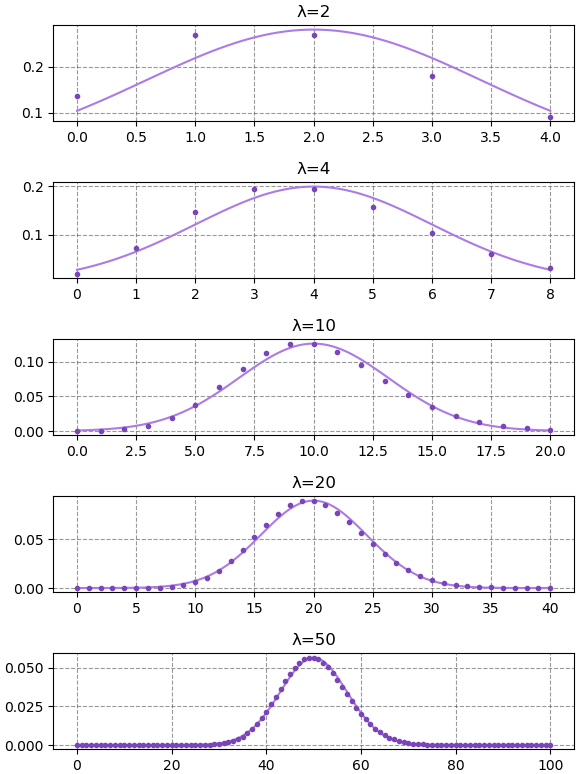
จะเห็นว่ายิ่ง λ มีค่ามากก็ยิ่งประมาณได้ใกล้เคียง
ทิ้งท้ายบท
ในบทที่ผ่านมาได้อธิบายถึงเรื่องความน่าจะเป็น และได้ยกตัวอย่างการแจกแจงชนิดต่างๆที่พบได้มาก ซึ่งเป็นแค่ส่วนหนึ่งเท่านั้น
ชนิดการแจกแจงความน่าจะเป็นนั้นจริงๆมีอยู่หลากหลายชนิดกว่านี้มากจนไม่อาจกล่าวได้หมด เช่น การแจกแจงลาปลาส (拉普拉斯分布, Laplace distribution), การแจกแจงเอฟ (F分布, F Distribution), การแจกแจงที (t分布, t Distribution), การแจกแจงไคกำลังสอง (χ²分布, Chi-Square Distribution) เป็นต้น
แต่ในบรรดาการแจกแจงทั้งหลายนั้นที่สำคัญที่สุดและใช้เป็นปกติมากที่สุดก็คือการแจกแจงแบบปกติ เพราะเกิดขึ้นได้ง่ายตามธรรมชาติ
และจะเห็นว่าการแจกแจงบางอย่างเช่นการแจกแจงทวินามและการแจกแจงปัวซงสามารถประมาณเป็นการแจกแจงแบบปกติได้ในเงื่อนไขดังที่ได้กล่าวมาแล้ว
และการแจกแจงแบบอื่นๆนั้นถ้าหากทำหลายครั้งแล้วนำมาเฉลี่ยกันหลายค่ามากก็จะค่อยๆกลายเป็นการแจกแจงแบบปกติไปตามทฤษฎีขีดจำกัดกลาง
เรื่องของการแจกแจงแบบปกตินั้นยังเชื่อมโยงไปสู่เรื่องอื่นๆซึ่งใช้ในทางสถิติ เช่น เรื่อง ความแปรปรวนร่วมเกี่ยว (协方差, covariance) และการแจกแจงแบบปกติหลายตัวแปร ซึ่งจะกล่าวถึงในบทถัดไป
บทถัดไป >> บทที่ ๑๓