opencv-python เบื้องต้น บทที่ ๗: การหมุนหรือบิดแปลงภาพ
เขียนเมื่อ 2020/06/28 18:50
แก้ไขล่าสุด 2024/02/22 10:26
ต่อจาก บทที่ ๖
ในบทนี้จะเป็นเรื่องของการแปลงภาพในลักษณะที่นำภาพมาบิดดัดหรือหมุน โดยฟังก์ชันหลักๆที่ใช้ก็คือ cv2.warpAffine() และ cv2.warpPerspective() และมีฟังก์ชันอื่นๆที่เป็นตัวช่วยเสริมคือ cv2.getAffineTransform() cv2.getRotationMatrix2D() cv2.getPerspectiveTransform()
การบิดแปลงภาพด้วยการคูณเมทริกซ์
cv2.warpAffine() เป็นฟังก์ชันสำหรับเอารูปภาพมาดัดบิดแปลงตำแหน่ง
เพื่อให้เห็นภาพว่าการบิดแปลงภาพนี้เป็นไปในลักษณะแบบไหนขอเริ่มจากตัวอย่างผลจากการบิดแปลงโดย cv2.warpAffine()
สมมุติว่ามีรูปนี้อยู่เป็นภาพตั้งต้น

พอใช้ cv2.warpAffine() แล้วก็จะถูกบิดแปลงรูปร่างได้หลากหลาย ยกตัวอย่าง ๗ ภาพนี้

จะเห็นว่ามีทั้งการหมุน พลิกกลับ ย่อขยาย รูปร่างจะถูกแปลงไปจากที่เดิมเป็นสี่เหลี่ยมผืนผ้า ก็กลายเป็นสี่เหลี่ยมด้านขนานไป
ต่อไปจะอธิบายหลักการ ซึ่งเป็นเรื่องของคณิตศาสตร์ วิธีที่ใช้ในการแปลงก็คือ การคูณเมทริกซ์
ถ้ามีจุดพิกัดอยู่จุดหนึ่งในรูปภาพ ๒ มิติ พิกัด (x1,y1) อาจเขียนเป็นเมทริกซ์ได้ว่า
โดยที่ 1 นี้เป็นแกน z ซึ่งจะให้เป็น 1 เสมอ เพราะจริงๆแล้วภาพมีแค่ ๒ มิติ ไม่ได้ต้องใช้มิติที่ ๓ แต่เพิ่มเข้ามาเพื่อใช้แทนมิติที่เป็นค่าคงที่
ถ้ามี n จุดก็เอาพิกัดของแต่ละจุดมาเขียนรวมกันเป็นเมทริกซ์แบบนี้
เมทริกซ์ที่ใช้บิดแปลงภาพด้วย cv2.warpAffine() คือเมทริกซ์ขนาด 2×3
เมทริกซ์ของพิกัดที่จะได้หลังแปลงนั้นจะได้มาจากการเอาเมทริกซ์การแปลงมาคูณเข้ากับเมทริกซ์พิกัดเดิม
ก็จะได้เมทริกซ์ของพิกัดใหม่
ค่าพิกัดใหม่ในแต่ละจุดเป็น
ลองสร้างเมทริกซ์ขึ้นมาโดยใช้อาเรย์ใน numpy แล้วทำการคูณเมทริกซ์ดูเป็นตัวอย่าง
import cv2
import numpy as np
import matplotlib.pyplot as plt
# เมทริกซ์พิกัด
X = np.array([[4,7,6], # x1,x2,x3
[1,2,4], # y1,y2,y3
[1,1,1]])
# เมทริกซ์การแปลง
M = np.array([[0,1,-1], # ax,bx,cx
[1,0,-1]]) # ay,by,cy
# แปลงเอาพิกัดใหม่
X2 = np.dot(M,X)
plt.axes(aspect=1)
# วาดจุดพิกัดเก่าและใหม่
plt.scatter(X[0],X[1],c='r',marker='x')
plt.scatter(X2[0],X2[1],c='m',marker='x')
for i in range(3): # วาดลูกศรที่ลากจากจุดเก่าไปใหม่
plt.arrow(X[0,i],X[1,i],X2[0,i]-X[0,i],X2[1,i]-X[1,i],head_width=0.2,head_length=0.4,length_includes_head=1,color='k')
plt.grid()
plt.show()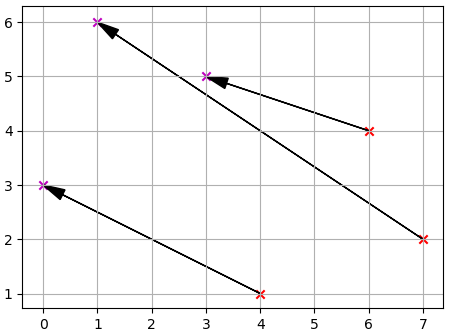
การใช้ cv2.warpAffine() จะเป็นการย้ายจุดทุกจุดพิกเซลบนภาพจากพิกัดเก่าไปพิกัดใหม่ในลักษณะเช่นนี้
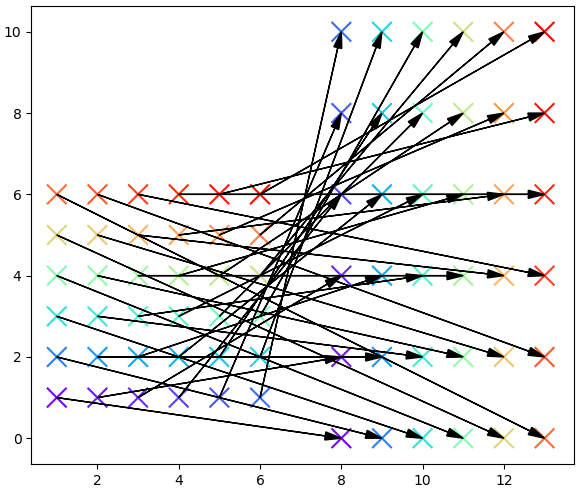
จากนั้นก็จะทำการประมาณค่าในช่วงโดยใช้หลักการเดียวกับตอนที่ย่อขยายรูป เพื่อหาค่าของแต่ละพิกเซลใหม่ แล้วก็จะได้ภาพใหม่ที่ถูกบิดไปจากตำแหน่งเดิม
วิธีใช้ฟังก์ชัน warpAffine
ฟังก์ชัน cv2.warpAffine() มีค่าที่ต้องใส่ดังนี้
| ลำดับ | ชื่อ | สิ่งที่ต้องใส่ | ชนิดข้อมูล |
|---|---|---|---|
| 1 | src | อาเรย์รูปภาพ | np.array |
| 2 | M | เมทริกซ์แปลง | np.array |
| 3 | dsize | ขนาดของภาพหลังแปลง | np.array |
ค่าที่จำเป็นต้องใส่คือ ๓ ตัวแรก คือตัวอาเรย์ภาพ เมทริกซ์ที่จะใช้แปลงภาพนั้น และขนาดของภาพที่ต้องการจะได้หลังแปลง
ขนาดของภาพในที่นี้เป็นตัวกำหนดขอบเขตของภาพที่จะเหลือหลังแปลง ถ้าแปลงแล้วบริเวณที่อยู่นอกกรอบจะหายไป เพื่อความง่ายอาจกำหนดให้ขนาดเท่ากับภาพเดิม แต่ว่าก็ไม่จำเป็น
นอกจากนี้มีคีย์เวิร์ดที่สามารถใส่เพิ่มเติมได้ คือ flags คือวิธีการประมาณค่าในช่วงใส่เป็นแฟล็กที่ขึ้นต้นด้วย cv2.INTER_ เช่นเดียวกับตอนที่ใช้ cv2.resize()
และ borderMode คือวิธีการเติมขอบ จะใช้แฟล็กที่ขึ้นต้นด้วย cv2.BORDER_ เช่นเดียวกับตอนใช้ cv2.copyMakeBorder()
ถ้าไม่ได้ใส่ borderMode จะได้เป็นพื้นสีดำ
เกี่ยวกับรายละเอียดตัวเลือกแฟล็กรูปแบบขอบและการประมาณค่าในช่วงนั้นดูได้ในบทที่ ๖
ตัวอย่าง

rin07c03.jpg
rin = cv2.imread('rin07c03.jpg')
mat = np.float32([[0.9,0.1,90],
[0.2,0.7,50]])
rin = cv2.warpAffine(rin,mat,(600,450))
plt.imshow(rin[:,:,::-1])
plt.show()
ลองเทียบวิธีการเติมขอบในแบบต่างๆ
rin = cv2.imread('rin07c03.jpg')
mat = np.float32([[0.4,-0.1,200],
[-0.2,0.5,150]])
title = ['replicate','reflect','reflect101','wrap']
border = [cv2.BORDER_REPLICATE,cv2.BORDER_REFLECT,cv2.BORDER_REFLECT101,cv2.BORDER_WRAP]
plt.figure(figsize=[6,5])
for i in range(4):
plt.subplot(221+i,title=title[i])
plt.imshow(cv2.warpAffine(rin,mat,(600,450),borderMode=border[i])[:,:,::-1])
plt.tight_layout()
plt.show()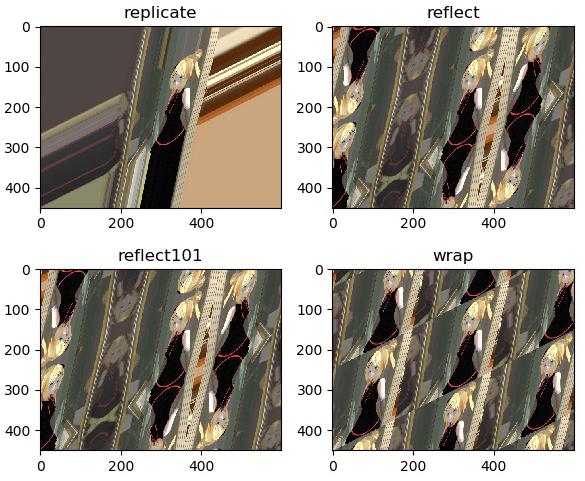
ตัวอย่างเมทริกซ์แปลงแบบง่ายๆ
จากตัวอย่างที่ยกมาจะเห็นว่าใส่เมทริกซ์แล้วภาพก็จะบิดแปลงรูปไปเป็นแบบต่างๆได้ แต่ว่าก็คงจะนึกภาพยากอยู่ว่าใส่ค่าอย่างไรลงไปแล้วจะเป็นการบิดแบบไหน
ดังนั้นต่อไปจะเป็นการยกตัวอย่างแสดงให้เห็นภาพคร่าวๆ ว่าในการแปลงแต่ละแบบต้องใช้เมทริกซ์ในลักษณะยังไงบ้าง
เริ่มจากการย่อหรือขยายภาพ ใส่แค่ค่า ax กับ by แบบนี้
ผลจะคล้ายกับการใช้ cv2.resize() แต่ขนาดและขอบเขตของภาพที่เหลืออยู่จะขึ้นอยู่กับที่กำหนด
ตัวอย่าง
rin = cv2.imread('rin07c03.jpg')
mat = np.float32([[0.6,0,0],
[0,0.4,0]])
plt.imshow(cv2.warpAffine(rin,mat,(600,450))[:,:,::-1])
plt.tight_layout()
plt.show()
การเลื่อนตำแหน่ง
rin = cv2.imread('rin07c03.jpg')
mat = np.float32([[1,0,-200],
[0,1,150]])
plt.imshow(cv2.warpAffine(rin,mat,(600,450))[:,:,::-1])
plt.tight_layout()
plt.show()
ทั้งเลื่อนตำแหน่งและย่อขยาย
rin = cv2.imread('rin07c03.jpg')
mat = np.float32([[0.5,0,100],
[0,0.5,100]])
plt.imshow(cv2.warpAffine(rin,mat,(600,450))[:,:,::-1])
plt.tight_layout()
plt.show()
สลับกลับแกน x,y
rin = cv2.imread('rin07c03.jpg')
mat = np.float32([[0,1,0],
[1,0,0]])
rin = cv2.warpAffine(rin,mat,(600,450))
plt.imshow(rin[:,:,::-1])
plt.tight_layout()
plt.show()
พลิกภาพ คล้ายการใช้ cv2.flip()
rin = cv2.imread('rin07c03.jpg')
plt.figure(figsize=[6,12])
mat = np.float32([[-1,0,600],
[0,1,0]])
plt.subplot(311)
plt.imshow(cv2.warpAffine(rin,mat,(600,450))[:,:,::-1])
mat = np.float32([[1,0,0],
[0,-1,450]])
plt.subplot(312)
plt.imshow(cv2.warpAffine(rin,mat,(600,450))[:,:,::-1])
mat = np.float32([[-1,0,600],
[0,-1,450]])
plt.subplot(313)
plt.imshow(cv2.warpAffine(rin,mat,(600,450))[:,:,::-1])
plt.tight_layout()
plt.show()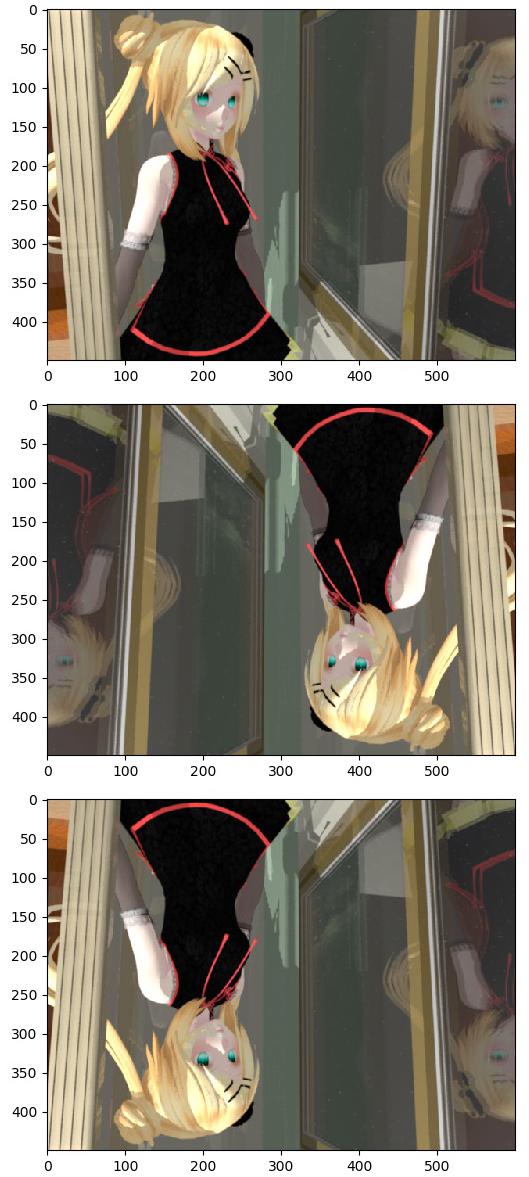
การนำภาพมาเฉือน
rin = cv2.imread('rin07c03.jpg')
plt.figure(figsize=[6,5])
mat = np.float32([[1,0.5,0],
[0,1,0]])
plt.subplot(221)
plt.imshow(cv2.warpAffine(rin,mat,(600,450))[:,:,::-1])
mat = np.float32([[1,0,0],
[0.5,1,0]])
plt.subplot(222)
plt.imshow(cv2.warpAffine(rin,mat,(600,450))[:,:,::-1])
mat = np.float32([[1,0.5,0],
[0.5,1,0]])
plt.subplot(223)
plt.imshow(cv2.warpAffine(rin,mat,(600,450))[:,:,::-1])
mat = np.float32([[1,-0.5,0],
[-0.5,1,0]])
plt.subplot(224)
plt.imshow(cv2.warpAffine(rin,mat,(600,450))[:,:,::-1])
plt.tight_layout()
plt.show()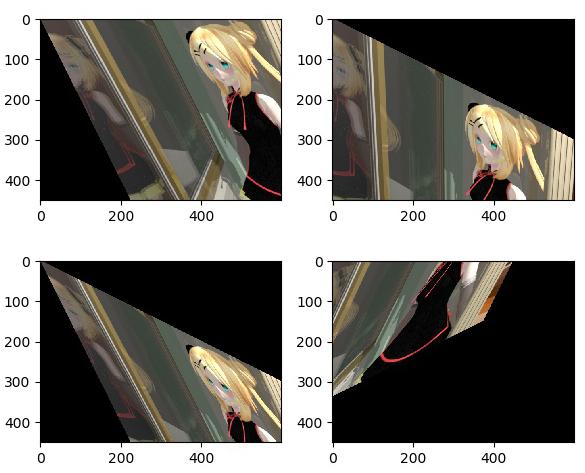
การสร้างเมทริกซ์สำหรับหมุนภาพ
จากตัวอย่างที่ผ่านมาจะเห็นว่ามีทั้งภาพที่ถูกบิดแปลงเปลี่ยนรูปไป หรือย่อขยายหรือพลิกกลับ แต่นอกจากนี้แล้ว cv2.warpAffine() สามารถใช้เพื่อหมุนภาพไปทั้งอย่างนั้นได้
กรณีที่ต้องการหมุนภาพ อาจกำหนดเมทริกซ์การแปลงเป็น
โดย θ คือขนาดของมุมที่ต้องการหมุนภาพ ตามเข็มนาฬิกา
เมทริกซ์แบบนี้เรียกว่าเป็น "เมทริกซ์การหมุน" (rotation matrix)
เมื่อใช้ลักษณะของเมทริกซ์การหมุน ทั้ง ๒ แกนจะถูกเฉือนโดยสัมพันธ์กัน ทำให้กลายเป็นการหมุนภาพโดยไม่มีการเปลี่ยนรูปได้
กรณีที่จุดศูนย์กลางไม่ใช่ (0,0) แต่อยู่ที่ (cx,cy) จะเพิ่มส่วนหลักที่ ๓ ลงไปเพื่อทำการย้ายตำแหน่งให้สัมพันธ์กันด้วย กลายเป็นเมทริกซ์แบบนี้
เมื่อ θ คือขนาดของมุมที่ต้องการหมุนภาพ ตามเข็มนาฬิกา
หากเราจะคำนวณเองเพื่อสร้างให้ได้เมทริกซ์แบบนั้นก็ทำได้ตามสมการข้างต้น แต่ว่าใน opencv ได้เตรียมฟังก์ชันสำหรับหาเมทริกซ์แบบนั้นให้โดยอัตโนมัติโดยไม่จำเป็นต้องเขียนเอง นั่นคือ cv2.getRotationMatrix2D()
ค่าที่ต้องใส่เป็นดังนี้
| ลำดับ | ชื่อ | สิ่งที่ต้องใส่ | ชนิดข้อมูล |
|---|---|---|---|
| 1 | center | จุดหมุน | np.array |
| 2 | angle | มุม (องศา) | float |
| 3 | scale | สัดส่วน | float |
เมื่อใช้ฟังก์ชันนี้แล้วก็จะได้เมทริกซ์การแปลงเพื่อหมุนตามแบบที่ต้องการ แล้วก็เอาเมทริกซ์นี้มาใช้กับ cv2.warpAffine() อีกที
ขณะหมุนสามารถย่อหรือขยายภาพไปด้วย ถ้าหากไม่ต้องการเปลี่ยนขนาดก็ให้ใส่ตัวที่ ๓ เป็น 1 ไป
ตัวอย่างการใช้ ลองเอาภาพมาหมุนด้วยมุมต่างๆกันดู

gumi07c01.jpg
gumi = cv2.imread('gumi07c01.jpg')
plt.figure(figsize=[6,4.5])
plt.subplot(221)
mat = cv2.getRotationMatrix2D((300,225),180,1)
plt.imshow(cv2.warpAffine(gumi,mat,(600,450))[:,:,::-1])
plt.subplot(222)
mat = cv2.getRotationMatrix2D((300,225),160,0.8)
plt.imshow(cv2.warpAffine(gumi,mat,(600,450))[:,:,::-1])
plt.subplot(223)
mat = cv2.getRotationMatrix2D((300,225),60,0.7)
plt.imshow(cv2.warpAffine(gumi,mat,(600,450))[:,:,::-1])
plt.subplot(224)
mat = cv2.getRotationMatrix2D((300,225),90,0.6)
plt.imshow(cv2.warpAffine(gumi,mat,(600,450))[:,:,::-1])
plt.tight_layout(0)
plt.show()
การสร้างเมทริกซ์สำหรับบิดแปลงภาพโดยการกำหนดจุดอ้างอิง
cv2.getAffineTransform() ใช้สร้างเมทริกซ์สำหรับที่จะนำมาใช้ใน cv2.warpAffine() โดยใช้วิธีการกำหนดจุดอ้างอิง ๓ จุดที่ต้องการย้าย
วิธีใช้คือกำหนดจุดอ้างอิงในพิกัดเดิมและพิกัดใหม่ ค่าที่ต้องใส่เป็นดังนี้
| ลำดับ | ชื่อ | สิ่งที่ต้องใส่ | ชนิดข้อมูล |
|---|---|---|---|
| 1 | src | จุดเดิม | np.array |
| 2 | dst | จุดใหม่ | np.array |
ตัวอย่างการใช้ เช่นลองเอาภาพนี้มาบิดโดยกำหนดจุดตรึงเดิมอยู่ที่มุม ๓ มุม แล้วกำหนดให้ย้ายไปอยู่จุดใหม่ที่เปลี่ยนไป

teto07c01.jpg
teto = cv2.imread('teto07c01.jpg')
xy1 = np.float32([[0,0],[0,450],[600,450]]) # จุดตรึงเดิม
xy2 = np.float32([[50,100],[150,400],[550,350]]) # จุดตรึงใหม่
mat = cv2.getAffineTransform(xy1,xy2) # สร้างเมทริกซ์แปลง
plt.figure(figsize=[5,7])
for i in [0,1]:
if(i==1):
teto = cv2.warpAffine(teto,mat,(600,450)) # ทำการแปลงภาพ
plt.subplot(211+i)
plt.imshow(teto[:,:,::-1])
plt.scatter(xy1[:,0],xy1[:,1],200,c='r',marker='*') # วาดจุดตรึงเดิม
plt.scatter(xy2[:,0],xy2[:,1],200,c='g',marker='*') # วาดจุดตรึงใหม่
plt.tight_layout(0)
plt.show()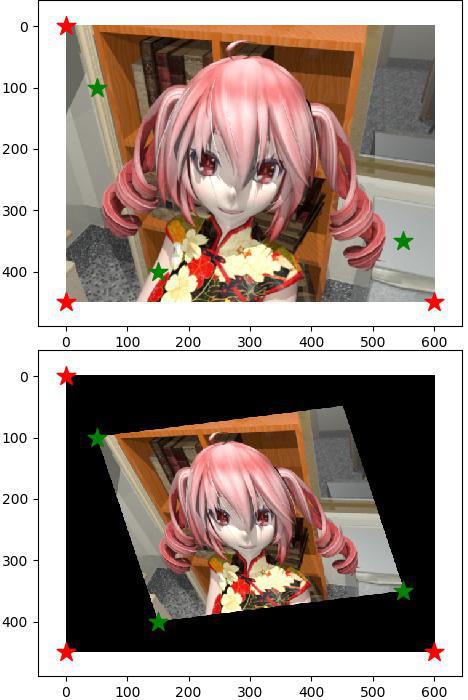
ในที่นี้ภาพบนคือภาพเดิม ภาพล่างคือภาพหลังแปลง จุดสีเขียวแสดงตำแหน่งจุดตรึงเดิม จุดสีแดงแสดงตำแหน่งจุดตรึงใหม่ จะเห็นว่ามุมที่กำหนดย้ายตำแหน่งจากจุดเดิมไปจุดใหม่ และส่วนอื่นก็ถูกแปลงให้สัมพันธ์กันไปตามนั้นด้วย
หรือถ้ามีภาพอะไรที่เป็นแผ่นสี่เหลี่ยมแต่ถูกถ่ายมาแบบเอียงๆ สามารถใช้วิธีนี้ปรับให้ตรงได้ ตัวอย่างเช่น

miku07c01.jpg
miku = cv2.imread('miku07c01.jpg')
xy1 = np.float32([[382,295],[545,354],[572,229]])
xy2 = np.float32([[205,300],[440,300],[445,150]])
plt.figure(figsize=[5,7])
ax1 = plt.subplot(211)
plt.imshow(miku[:,:,::-1])
ax2 = plt.subplot(212)
miku = cv2.warpAffine(miku,cv2.getAffineTransform(xy1,xy2),(600,450))
plt.imshow(miku[:,:,::-1])
for (x1,y1),(x2,y2) in zip(xy1,xy2):
ax1.plot((x1,x2),(y1,y2),'c')
ax1.scatter((x1,x2),(y1,y2),c=[(1,0.2,1),(0,1,0)],marker='*')
ax2.scatter([x2],[y2],c=[(0,1,0)],marker='*')
plt.tight_layout(0)
plt.show()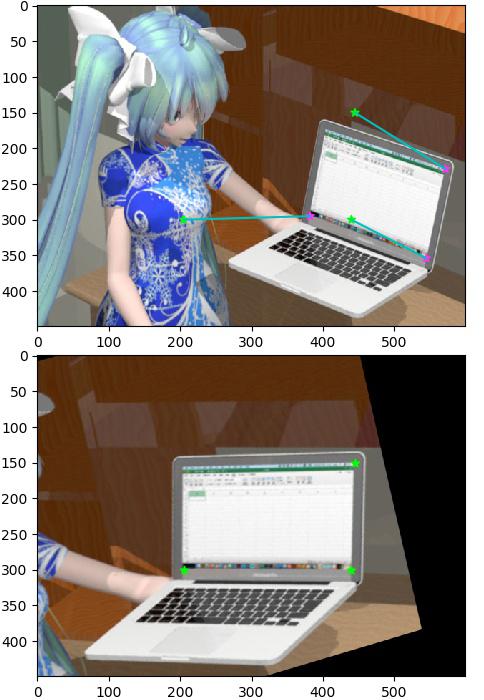
การแปลงภาพเป็นสามมิติหรือแปลงกลับ
ใน opencv มีฟังก์ชันที่ทำงานคล้ายกับ cv2.warpAffine() แต่ซับซ้อนขึ้นกว่า นั่นคือ cv2.warpPerspective()
วิธีการใช้จะคล้ายกับ cv2.warpAffine() แต่จะเป็นการคูณด้วยอาเรย์ขนาด 3×3 แทน ซึ่งจะทำให้แปลงรูปได้หลากหลายขึ้นกว่าเดิม
การแปลงโดยใช้ cv2.warpAffine() นั้นจะเป็นการเฉือนในลักษณะตรึงจุด ๓ จุดแล้วเลื่อนไป วิธีการนี้อาจสามารถบิดดัดภาพได้หลากหลาย แต่ก็ยังมีข้อจำกัดอยู่ เพราะรูปสี่เหลี่ยมมี ๔ มุม เมื่อบิดโดยตรึงแค่ ๓ จุดแบบนี้ อีกมุมก็จะถูกกำหนดตายตัวโดยให้มีรูปร่างสมมาตรไป ผลที่ได้จากสี่เหลี่ยมผืนผ้าก็จะเป็นสี่เหลี่ยมด้านขนาน
ในบางกรณีเช่นเมื่อต้องการดัดแปลงภาพให้ดูเหมือนเป็น ๓ มิติจริงๆนั้นจำเป็นต้องใช้จุดตรึง ๔ จุด ซึ่ง cv2.warpPerspective() สามารถทำแบบนั้นได้
เช่นเดียวกับที่ cv2.warpAffine() ใช้ฟังก์ชัน cv2.getAffineTransform() ในการสร้างเมทริกซ์แปลงขึ้นจากจุด ๓ จุด สำหรับ cv2.warpPerspective() เองก็มีฟังก์ชันที่ใช้คู่กันคือ cv2.getPerspectiveTransform() ซึ่งทำงานคล้ายกันแต่จะใช้จุดตรึง ๔ ผลที่ได้อาจออกมาเป็นสี่เหลี่ยมด้านไม่เท่า แล้วแต่ตำแหน่งมุมที่กำหนด จุด
ตัวอย่างการใช้ ลองทำเช่นเดียวกับตอนใช้ cv2.warpAffine() คือเอาภาพมาบิดตามจุดตรึง

teto07c03.jpg
teto = cv2.imread('teto07c03.jpg')
xy1 = np.float32([[0,0],[0,450],[600,450],[600,0]]) # จุดตรึงเดิม
xy2 = np.float32([[100,120],[160,380],[450,350],[440,10]]) # จุดตรึงใหม่
mat = cv2.getPerspectiveTransform(xy1,xy2) # สร้างเมทริกซ์แปลง
plt.figure(figsize=[5,7])
for i in [0,1]:
if(i==1):
teto = cv2.warpPerspective(teto,mat,(600,450)) # ทำการแปลงภาพ
plt.subplot(211+i)
plt.imshow(teto[:,:,::-1])
plt.scatter(xy1[:,0],xy1[:,1],200,c='r',marker='*') # วาดจุดตรึงเดิม
plt.scatter(xy2[:,0],xy2[:,1],200,c='g',marker='*') # วาดจุดตรึงใหม่
plt.tight_layout(0)
plt.show()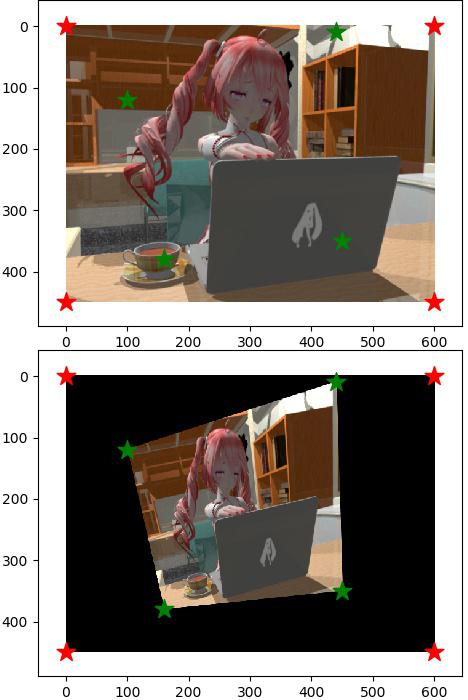
จะเห็นว่าเมื่อใช้วิธีนี้แล้วจะบิดแปลงเป็นรูปสี่เหลี่ยมใดๆก็ได้ และแน่นอนว่าในทางกลับกันก็ดัดรูปที่เป็นสี่เหลี่ยมด้านไม่เท่าให้เป็นสี่เหลี่ยมด้านขนานได้
สุดท้ายลองดูตัวอย่างการนำเอาภาพหน้าจอสี่เหลี่ยมที่ถูกถ่ายในสามมิติมาแปลงกลับเป็นแผ่นสี่เหลี่ยมผืนผ้า

teto07c05.jpg
teto = cv2.imread('teto07c05.jpg')
xy1 = np.float32([[37,122],[116,412],[342,273],[289,55]])
xy2 = np.float32([[0,0],[0,450],[600,450],[600,0]])
mat = cv2.getPerspectiveTransform(xy1,xy2)
cv2.imwrite('teto07c06.jpg',cv2.warpPerspective(teto,mat,(600,450)))
teto07c06.jpg
อ่านบทถัดไป >> บทที่ ๘
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> opencv-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib