numpy & matplotlib เบื้องต้น บทที่ ๒: การใช้อาเรย์เบื้องต้น
เขียนเมื่อ 2016/06/11 11:13
แก้ไขล่าสุด 2021/09/28 16:42
numpy เป็นมอดูลที่ทำให้เราสามารถใช้ออบเจ็กต์ชนิดที่เรียกว่า ndarray ซึ่งหมายถึงอาเรย์หลายมิติ บางครั้งก็เรียกว่าอาเรย์เฉยๆ
คำว่า "อาเรย์" นั้นเป็นคำที่ถูกใช้ในภาษาอื่นๆอีกหลายภาษา เช่น ภาษาซี, php, จาวาสคริปต์, รูบี เป็นต้น แต่ว่าสำหรับในภาษาไพธอนสิ่งที่มีคุณสมบัติเทียบเท่ากับอาเรย์ในภาษาอื่น นั้นกลับเรียกว่าลิสต์ ส่วนอาเรย์จะหมายถึง ndarray ของ numpy
ในมอดูลมาตรฐานของภาษาไพธอนก็มีสิ่งที่เรียกว่าอาเรย์อยู่ แต่ก็ไม่เป็นที่นิยมใช้ ดังนั้นพอพูดถึงอาเรย์ในภาษาไพธอนแล้วจึงมักหมายถึง ndarray ของ numpy นั่นเอง
ก่อนที่จะเริ่มใช้งานสิ่งที่ต้องทำเป็นอย่างแรกก็คือทำการ import เรียกใช้ขึ้นมาก่อน
ตัวย่อ np นี้จะใช้แบบนี้ไปตลอดในบทความทุกบท เพราะค่อนข้างเป็นสากล แม้แต่เวลาที่เรียกชื่อฟังก์ชันต่างๆใน numpy ก็จะเรียกโดยขึ้นต้นด้วย np.
การสร้างอาเรย์ขึ้นจากลิสต์
มีอยู่หลายวิธีในการสร้างอาเรย์ แต่วิธีที่พื้นฐานที่สุดคือสร้างขึ้นมาจากลิสต์, ทูเพิล หรือเรนจ์ โดยใช้ np.array(ลิสต์)
ได้
เท่านี้ก็จะได้อาเรย์ขึ้นมาตามที่ต้องการ ถ้าดูเผินๆจะเห็นว่าไม่ต่างอะไรจากลิสต์นัก แต่ความจริงแล้วต่างไปพอสมควร
ที่อาจจะเห็นได้เป็นอย่างแรกก็คือเวลาที่สั่ง print จะออกมาเป็นแถวเป็นระเบียบร้อยอย่างที่เห็นโดยอัตโนมัติ ทำให้ดูเข้าใจง่ายขึ้นมาก
อย่างต่อมาคืออาเรย์มีแอตทริบิวต์ติดตัวที่สามารถให้ข้อมูลของตัวอาเรย์นั้น เช่น
ลองเอาอาเรย์ ๒ ตัวจากตัวอย่างเมื่อครู่มาหาแอตทริบิวต์
นอกจากนี้ยังสามารถใช้ฟังก์ชันที่ชื่อเหมือนกับแอตทริบิวต์เหล่านี้ในการหาค่าได้ด้วย ผลที่ได้จะเหมือนกัน
จะเห็นว่ากรณีที่ลิสต์ที่ใช้นั้นมีการซ้อนกันก็จะได้เป็นอาเรย์ ๒ มิติ โดยมีแนวตั้งเป็นมิติที่หนึ่ง แนวนอนเป็นมิติที่สอง
และยังสามารถซ้อนกันเป็นมิติที่สูงขึ้นไปอีกได้ เช่นลองสร้าง ๓ มิติ
ได้
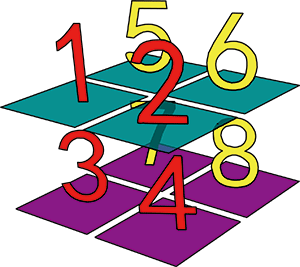
โดยมิติที่สามนั้นหากนำมาวาดเป็นรูปแล้วละก็อาจแสดงได้ในรูปของแถวในแนวลึกที่เพิ่มเข้ามา
สำหรับ สี่มิติขึ้นไปจะเริ่มอยู่เหนือสามัญสำนึกของคนทั่วไป งานที่จะต้องใช้มิติมากขนาดนั้นก็มักจะค่อนข้างเฉพาะทาง ดังนั้นจะไม่ขอกล่าวถึง
เนื้อหาส่วนใหญ่ในบทต้นๆจะเน้นหนึ่งถึงสองมิติเป็นหลัก และสำหรับสามมิติจะเริ่มเน้นในบทที่ ๒๓
มีข้อควรระวังคือลิสต์ที่จะใช้สร้างอาเรย์จะต้องมีจำนวนสมาชิกในลิสต์ย่อยแต่ละลิสต์เท่ากันไม่เช่นนั้นจะถูกตีความเป็นออบเจ็กต์ทั่วไป
จะเห็นว่าผลที่ได้คือมันกลายเป็นอาเรย์มิติเดียวซึ่งมีขนาดเป็น 2 นั่นเพราะ [1,2] และ [3,4,5] ถูกตีความเป็นออบเจ็กต์อย่างละชิ้น แทนทีจะคิดเป็นตัวๆแยกกัน
ชนิดของข้อมูลในอาเรย์
สามารถตรวจสอบชนิดของข้อมูลในอาเรย์ได้โดยดูที่แอตทริบิวต์ชื่อ dtype
เช่นลองใช้อาเรย์ที่สร้างในตัวอย่างก่อน
จะเห็นว่า arayu ซึ่งสร้างขึ้นมาจากลิสต์ที่มีจำนวนสมาชิกไม่เท่ากันนั้นได้ข้อมูลประเภท object แทนที่จะเป็น int อย่างที่ควรเป็น
ส่วน araye นั้นกลายเป็นชนิด int ตามที่ควรจะเป็น โดยเลข 64 ใน int64 นี้บอกถึงขนาดของหน่วยความจำเป็นบิตที่ใช้ในการเก็บตัวเลข ปกติแล้วในภาษาไพธอนจำนวนเต็มจะไม่ได้แบ่งชนิดย่อย แต่ในบางภาษาเช่นภาษาซีจำนวนเต็มจะถูกแบ่งเป็นชนิดตามขนาดของหน่วยความจำที่ ใช้
ปกติแล้วถ้าไม่ได้ระบุอะไรข้อมูลจำนวนเต็มจะถูกตั้งให้เป็น int64 ซึ่งเป็นขนาดใหญ่สุด นอกจาก int64 แล้วก็ยังมี int8 int16 int32 ซึ่งจะกินพื้นที่น้อยกว่า และ float เองก็มีแบ่งเช่นกัน
ชนิดของข้อมูลสามารถกำหนดได้ตอนที่สร้างอาเรย์ขึ้นมา โดยเพิ่มคีย์เวิร์ด dtype เข้าไป
ถ้าตอนสร้างมีสมาชิกที่มีทศนิยมแม้แต่ตัวเดียวทั้งหมดก็จะกลายเป็น float64 ทันที
จะเห็นว่าข้อมูลในอาเรย์จะต้องประกอบจากตัวแปรชนิดเดียวกันหมดทุกตัว หากตอนที่สร้างอาเรย์ขึ้นจากลิสต์นั้นมีสมาชิกที่ชนิดต่างกันจะถูกทำให้เหมือนกันหมด
กรณีที่มีสายอักขระปนอยู่ตัวอื่นก็จะถูกเปลี่ยนเป็นสายอักขระไปด้วย เช่น
ได้
U ในที่นี้หมายถึงเป็นยูนิโค้ด และ 32 เป็นจำนวนหน่วยความจำที่ใช้ โดยปกติจะเท่ากับจำนวนตัวอักษรแต่ถ้าสั้นกว่า 32 จะถูกกำหนดให้เป็น 32
ใน ภาษาซีเวลาที่ประกาศตัวแปรชนิดสายอักขระจะต้องกำหนดความยาวไว้ตายตัว ดังนั้นอาเรย์ซึ่งตั้งอยู่บนพื้นฐานของภาษาซีจึงมีลักษณะการจัดเก็บข้อมูลใน ลักษณะนี้ไปด้วย
อนึ่ง
ความยาวของสายอักขระสามารถกำหนดขึ้นเองได้ และถ้ากำหนดความยาวต่ำกว่าจำนวนตัวอักษรก็จะถูกตัดทอนหายไป
นี่เป็นเนื้อหาที่เกี่ยวเนื่องมาจากภาษาซี จะไม่เน้นมาก ณ ที่นี้เพราะงานหลักของอาเรย์ที่จะใช้คือใช้กับตัวเลขเพื่อคำนวณ
อาเรย์สามารถเก็บข้อมูลชนิดสายอักขระได้ก็จริง แต่โดยทั่วไปมักจะใช้กับจำนวนตัวเลขมากกว่า เพื่อที่จะใช้ประโยชน์ในเรื่องการคำนวณอย่างเต็มที่
ชนิดของอาเรย์ทั้งหมดสามารถดูได้ที่แอตทริบิวต์ np.sctypes
ผลลัพธ์
ชนิดของสมาชิกในอาเรย์สามารถเปลี่ยนได้ด้วยเมธอด astype บนตัวอาเรย์
การอ้างอิงถึงข้อมูลในอาเรย์
เช่น เดียวกับลิสต์ อาเรย์ก็ใช้การเติมวงเล็บเหลี่ยม [ ] เพื่ออ้างอิงข้อมูล โดยเลขในกรณีสองมิตินั้น ตัวแรกคือดัชนีของแนวตั้ง (เลขแถว) และตัวหลังคือแนวนอน (เลขหลัก)
แต่นอกจากนั้นแล้วยังสามารถเขียนโดยใช้เป็นคู่อันดับโดยมีจุลภาค , คั่นในวงเล็บเหลี่ยมตัวเดียวแทนการใส่วงเล็บเหลี่ยมสองอันได้ด้วย ซึ่งแบบนี้ลิสต์ไม่สามารถทำได้
การเข้าถึงสมาชิกทีละหลายตัวก็ทำได้ด้วยการใช้โคลอน : เช่นเดียวกับลิสต์ แต่สำหรันอาเรย์สองมิติแทนที่จะใช้วงเล็บเหลี่ยมวางต่อกันสองอันสามารถใช้จุลภาคแทนได้เช่นกัน

ซึ่งการที่ใช้จุลภาคแทนได้นั้นมีข้อดีคือเข้าถึงสมาชิกที่อยู่ในหลัก (แนวตั้ง) เดียวกันแต่คนละแถว (แนวนอน) โดยการใส่ : ไว้ทางซ้าย
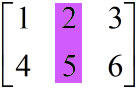
ซึ่งจะเห็นได้ว่าการใช้วงเล็บเหลี่ยมคู่ [ ][ ] จะวาง [:] ไว้ซ้ายหรือขวาก็ให้ผลไม่ต่างจากเดิม คือให้สมาชิกที่อยู่ในแถวแนวนอนแถวเดียวกันเท่านั้น
จะเห็นว่า [1,:] กับ [1][:] และ [:][1] ให้ผลเหมือนกัน แต่ [:,1] เท่านั้นที่จะให้ผลต่าง
ถ้าลองสร้างลิสต์แบบเดียวกันมาโดยไม่แปลงเป็นอาเรย์จะพบว่าไม่สามารถทำในสิ่งเดียวกันได้
สรุปเป็นตารางเพื่อให้เห็นภาพชัด สมมุติว่าอาเรย์มี n แถว m หลัก
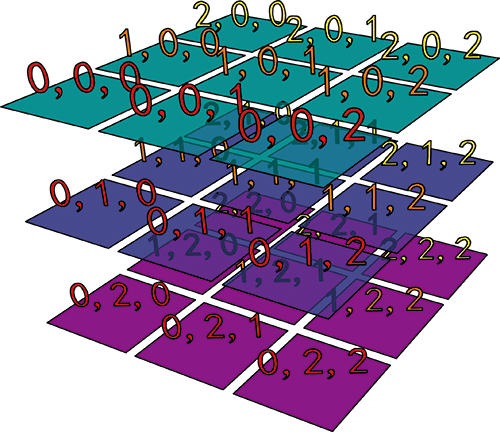
สำหรับสามมิติซึ่งมีขนาด 3,3,3 อาจเขียนได้ดังนี้
การวางตัวเลขไว้หน้าและหลัง : เพื่อคัดเลือกอาเรย์เฉพาะในช่วงที่ต้องการก็ทำได้เช่นเดียวกับลิสต์
ตัวอย่างกรณีหนึ่งมิติ
คำว่า "อาเรย์" นั้นเป็นคำที่ถูกใช้ในภาษาอื่นๆอีกหลายภาษา เช่น ภาษาซี, php, จาวาสคริปต์, รูบี เป็นต้น แต่ว่าสำหรับในภาษาไพธอนสิ่งที่มีคุณสมบัติเทียบเท่ากับอาเรย์ในภาษาอื่น นั้นกลับเรียกว่าลิสต์ ส่วนอาเรย์จะหมายถึง ndarray ของ numpy
ในมอดูลมาตรฐานของภาษาไพธอนก็มีสิ่งที่เรียกว่าอาเรย์อยู่ แต่ก็ไม่เป็นที่นิยมใช้ ดังนั้นพอพูดถึงอาเรย์ในภาษาไพธอนแล้วจึงมักหมายถึง ndarray ของ numpy นั่นเอง
ก่อนที่จะเริ่มใช้งานสิ่งที่ต้องทำเป็นอย่างแรกก็คือทำการ import เรียกใช้ขึ้นมาก่อน
import numpy as np
ตัวย่อ np นี้จะใช้แบบนี้ไปตลอดในบทความทุกบท เพราะค่อนข้างเป็นสากล แม้แต่เวลาที่เรียกชื่อฟังก์ชันต่างๆใน numpy ก็จะเรียกโดยขึ้นต้นด้วย np.
การสร้างอาเรย์ขึ้นจากลิสต์
มีอยู่หลายวิธีในการสร้างอาเรย์ แต่วิธีที่พื้นฐานที่สุดคือสร้างขึ้นมาจากลิสต์, ทูเพิล หรือเรนจ์ โดยใช้ np.array(ลิสต์)
aray = np.array(range(3,7))
araya = np.array([[1,2],[3,4]])
print(aray)
print(araya)
araya = np.array([[1,2],[3,4]])
print(aray)
print(araya)
ได้
[3 4 5 6]
[[1 2]
[3 4]]
[[1 2]
[3 4]]
เท่านี้ก็จะได้อาเรย์ขึ้นมาตามที่ต้องการ ถ้าดูเผินๆจะเห็นว่าไม่ต่างอะไรจากลิสต์นัก แต่ความจริงแล้วต่างไปพอสมควร
ที่อาจจะเห็นได้เป็นอย่างแรกก็คือเวลาที่สั่ง print จะออกมาเป็นแถวเป็นระเบียบร้อยอย่างที่เห็นโดยอัตโนมัติ ทำให้ดูเข้าใจง่ายขึ้นมาก
อย่างต่อมาคืออาเรย์มีแอตทริบิวต์ติดตัวที่สามารถให้ข้อมูลของตัวอาเรย์นั้น เช่น
| shape | รูปร่างของอาเรย์ |
| size | จำนวนสมาชิกในอาเรย์ |
| ndim | จำนวนมิติของอาเรย์ |
ลองเอาอาเรย์ ๒ ตัวจากตัวอย่างเมื่อครู่มาหาแอตทริบิวต์
print(aray.shape) # ได้ (4,)
print(aray.size) # ได้ 4
print(aray.ndim) # ได้ 1
print(araya.shape) # ได้ (2, 2)
print(araya.size) # ได้ 4
print(araya.ndim) # ได้ 2
print(aray.size) # ได้ 4
print(aray.ndim) # ได้ 1
print(araya.shape) # ได้ (2, 2)
print(araya.size) # ได้ 4
print(araya.ndim) # ได้ 2
นอกจากนี้ยังสามารถใช้ฟังก์ชันที่ชื่อเหมือนกับแอตทริบิวต์เหล่านี้ในการหาค่าได้ด้วย ผลที่ได้จะเหมือนกัน
print(np.size(araya))
print(np.shape(araya))
print(np.ndim(araya))
print(np.shape(araya))
print(np.ndim(araya))
จะเห็นว่ากรณีที่ลิสต์ที่ใช้นั้นมีการซ้อนกันก็จะได้เป็นอาเรย์ ๒ มิติ โดยมีแนวตั้งเป็นมิติที่หนึ่ง แนวนอนเป็นมิติที่สอง
และยังสามารถซ้อนกันเป็นมิติที่สูงขึ้นไปอีกได้ เช่นลองสร้าง ๓ มิติ
araye = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
print(araye)
print(araye.shape)
print(araye.size)
print(araye.ndim)
print(araye)
print(araye.shape)
print(araye.size)
print(araye.ndim)
ได้
[[[1 2]
[3 4]]
[[5 6]
[7 8]]]
(2, 2, 2)
8
3
[3 4]]
[[5 6]
[7 8]]]
(2, 2, 2)
8
3
โดยมิติที่สามนั้นหากนำมาวาดเป็นรูปแล้วละก็อาจแสดงได้ในรูปของแถวในแนวลึกที่เพิ่มเข้ามา

สำหรับ สี่มิติขึ้นไปจะเริ่มอยู่เหนือสามัญสำนึกของคนทั่วไป งานที่จะต้องใช้มิติมากขนาดนั้นก็มักจะค่อนข้างเฉพาะทาง ดังนั้นจะไม่ขอกล่าวถึง
เนื้อหาส่วนใหญ่ในบทต้นๆจะเน้นหนึ่งถึงสองมิติเป็นหลัก และสำหรับสามมิติจะเริ่มเน้นในบทที่ ๒๓
มีข้อควรระวังคือลิสต์ที่จะใช้สร้างอาเรย์จะต้องมีจำนวนสมาชิกในลิสต์ย่อยแต่ละลิสต์เท่ากันไม่เช่นนั้นจะถูกตีความเป็นออบเจ็กต์ทั่วไป
arayu = np.array([[1,2],[3,4,5]])
print(arayu.shape) # ได้ (2,)
print(arayu.size) # ได้ 2
print(arayu.ndim) # ได้ 1
print(arayu.shape) # ได้ (2,)
print(arayu.size) # ได้ 2
print(arayu.ndim) # ได้ 1
จะเห็นว่าผลที่ได้คือมันกลายเป็นอาเรย์มิติเดียวซึ่งมีขนาดเป็น 2 นั่นเพราะ [1,2] และ [3,4,5] ถูกตีความเป็นออบเจ็กต์อย่างละชิ้น แทนทีจะคิดเป็นตัวๆแยกกัน
ชนิดของข้อมูลในอาเรย์
สามารถตรวจสอบชนิดของข้อมูลในอาเรย์ได้โดยดูที่แอตทริบิวต์ชื่อ dtype
เช่นลองใช้อาเรย์ที่สร้างในตัวอย่างก่อน
araye = np.array([[[1,2],[3,4]],[[5,6],[7,8]]])
arayu = np.array([[1,2],[3,4,5]])
print(araye.dtype) # ได้ int64
print(arayu.dtype) # ได้ object
arayu = np.array([[1,2],[3,4,5]])
print(araye.dtype) # ได้ int64
print(arayu.dtype) # ได้ object
จะเห็นว่า arayu ซึ่งสร้างขึ้นมาจากลิสต์ที่มีจำนวนสมาชิกไม่เท่ากันนั้นได้ข้อมูลประเภท object แทนที่จะเป็น int อย่างที่ควรเป็น
ส่วน araye นั้นกลายเป็นชนิด int ตามที่ควรจะเป็น โดยเลข 64 ใน int64 นี้บอกถึงขนาดของหน่วยความจำเป็นบิตที่ใช้ในการเก็บตัวเลข ปกติแล้วในภาษาไพธอนจำนวนเต็มจะไม่ได้แบ่งชนิดย่อย แต่ในบางภาษาเช่นภาษาซีจำนวนเต็มจะถูกแบ่งเป็นชนิดตามขนาดของหน่วยความจำที่ ใช้
ปกติแล้วถ้าไม่ได้ระบุอะไรข้อมูลจำนวนเต็มจะถูกตั้งให้เป็น int64 ซึ่งเป็นขนาดใหญ่สุด นอกจาก int64 แล้วก็ยังมี int8 int16 int32 ซึ่งจะกินพื้นที่น้อยกว่า และ float เองก็มีแบ่งเช่นกัน
ชนิดของข้อมูลสามารถกำหนดได้ตอนที่สร้างอาเรย์ขึ้นมา โดยเพิ่มคีย์เวิร์ด dtype เข้าไป
ari = np.array([1,2,3,4],dtype='int16')
ariy = np.array([1,2,3,4],dtype='float32')
print(ariy) # ได้ [ 1. 2. 3. 4.]
ariy = np.array([1,2,3,4],dtype='float32')
print(ariy) # ได้ [ 1. 2. 3. 4.]
ถ้าตอนสร้างมีสมาชิกที่มีทศนิยมแม้แต่ตัวเดียวทั้งหมดก็จะกลายเป็น float64 ทันที
arey = np.array([1,2,3.14,4])
print(arey) # ได้ [ 1. 2. 3.14 4. ]
print(arey.dtype) # ได้ float64
print(arey) # ได้ [ 1. 2. 3.14 4. ]
print(arey.dtype) # ได้ float64
จะเห็นว่าข้อมูลในอาเรย์จะต้องประกอบจากตัวแปรชนิดเดียวกันหมดทุกตัว หากตอนที่สร้างอาเรย์ขึ้นจากลิสต์นั้นมีสมาชิกที่ชนิดต่างกันจะถูกทำให้เหมือนกันหมด
กรณีที่มีสายอักขระปนอยู่ตัวอื่นก็จะถูกเปลี่ยนเป็นสายอักขระไปด้วย เช่น
arayo = np.array([[1,2],[3.,'4']])
print(arayo)
print(arayo.dtype)
print(arayo)
print(arayo.dtype)
ได้
[['1' '2']
['3.0' '4']]
<U32
['3.0' '4']]
<U32
U ในที่นี้หมายถึงเป็นยูนิโค้ด และ 32 เป็นจำนวนหน่วยความจำที่ใช้ โดยปกติจะเท่ากับจำนวนตัวอักษรแต่ถ้าสั้นกว่า 32 จะถูกกำหนดให้เป็น 32
ใน ภาษาซีเวลาที่ประกาศตัวแปรชนิดสายอักขระจะต้องกำหนดความยาวไว้ตายตัว ดังนั้นอาเรย์ซึ่งตั้งอยู่บนพื้นฐานของภาษาซีจึงมีลักษณะการจัดเก็บข้อมูลใน ลักษณะนี้ไปด้วย
อนึ่ง
ความยาวของสายอักขระสามารถกำหนดขึ้นเองได้ และถ้ากำหนดความยาวต่ำกว่าจำนวนตัวอักษรก็จะถูกตัดทอนหายไป
print(np.array([[123456789]],dtype='<U5')) # ได้ [['12345']]
นี่เป็นเนื้อหาที่เกี่ยวเนื่องมาจากภาษาซี จะไม่เน้นมาก ณ ที่นี้เพราะงานหลักของอาเรย์ที่จะใช้คือใช้กับตัวเลขเพื่อคำนวณ
อาเรย์สามารถเก็บข้อมูลชนิดสายอักขระได้ก็จริง แต่โดยทั่วไปมักจะใช้กับจำนวนตัวเลขมากกว่า เพื่อที่จะใช้ประโยชน์ในเรื่องการคำนวณอย่างเต็มที่
ชนิดของอาเรย์ทั้งหมดสามารถดูได้ที่แอตทริบิวต์ np.sctypes
print(np.sctypes)
ผลลัพธ์
{'int': [<class 'numpy.int8'>, <class 'numpy.int16'>, , <class 'numpy.int64'>], 'uint': [, <class 'numpy.uint16'>, , <class 'numpy.uint64'>], 'others': [, <class 'object'>, <class 'str'>, , <class 'numpy.void'>], 'float': [, <class 'numpy.float32'>, , <class 'numpy.float128'>], 'complex': [<class 'numpy.complex64'>, <class 'numpy.complex128'>, <class 'numpy.complex256'>]}
ชนิดของสมาชิกในอาเรย์สามารถเปลี่ยนได้ด้วยเมธอด astype บนตัวอาเรย์
x = np.array([3.5,4.7,9,11.3,15])
print(x) # ได้ [ 3.5 4.7 9. 11.3 15. ]
print(x.astype(int)) # ได้ [ 3 4 9 11 15]
print(x.astype(str)) # ได้ ['3.5' '4.7' '9.0' '11.3' '15.0']
print(x) # ได้ [ 3.5 4.7 9. 11.3 15. ]
print(x.astype(int)) # ได้ [ 3 4 9 11 15]
print(x.astype(str)) # ได้ ['3.5' '4.7' '9.0' '11.3' '15.0']
การอ้างอิงถึงข้อมูลในอาเรย์
เช่น เดียวกับลิสต์ อาเรย์ก็ใช้การเติมวงเล็บเหลี่ยม [ ] เพื่ออ้างอิงข้อมูล โดยเลขในกรณีสองมิตินั้น ตัวแรกคือดัชนีของแนวตั้ง (เลขแถว) และตัวหลังคือแนวนอน (เลขหลัก)
ariyu = np.array([[1,2,3],[4,5,6]])
print(ariyu[0][1]) # ได้ 2
print(ariyu[1][2]) # ได้ 6
print(ariyu[0][1]) # ได้ 2
print(ariyu[1][2]) # ได้ 6
แต่นอกจากนั้นแล้วยังสามารถเขียนโดยใช้เป็นคู่อันดับโดยมีจุลภาค , คั่นในวงเล็บเหลี่ยมตัวเดียวแทนการใส่วงเล็บเหลี่ยมสองอันได้ด้วย ซึ่งแบบนี้ลิสต์ไม่สามารถทำได้
print(ariyu[0,2]) # ได้ 3
print(ariyu[1,1]) # ได้ 5
print(ariyu[1,1]) # ได้ 5
การเข้าถึงสมาชิกทีละหลายตัวก็ทำได้ด้วยการใช้โคลอน : เช่นเดียวกับลิสต์ แต่สำหรันอาเรย์สองมิติแทนที่จะใช้วงเล็บเหลี่ยมวางต่อกันสองอันสามารถใช้จุลภาคแทนได้เช่นกัน
print(ariyu[1][:]) # ได้ [4 5 6]
print(ariyu[1,:]) # ได้ [4 5 6]
print(ariyu[1,:]) # ได้ [4 5 6]

ซึ่งการที่ใช้จุลภาคแทนได้นั้นมีข้อดีคือเข้าถึงสมาชิกที่อยู่ในหลัก (แนวตั้ง) เดียวกันแต่คนละแถว (แนวนอน) โดยการใส่ : ไว้ทางซ้าย
print(ariyu[:,1]) # ได้ [2 5]

ซึ่งจะเห็นได้ว่าการใช้วงเล็บเหลี่ยมคู่ [ ][ ] จะวาง [:] ไว้ซ้ายหรือขวาก็ให้ผลไม่ต่างจากเดิม คือให้สมาชิกที่อยู่ในแถวแนวนอนแถวเดียวกันเท่านั้น
print(ariyu[:][1]) # ได้ [4 5 6]]
จะเห็นว่า [1,:] กับ [1][:] และ [:][1] ให้ผลเหมือนกัน แต่ [:,1] เท่านั้นที่จะให้ผลต่าง
ถ้าลองสร้างลิสต์แบบเดียวกันมาโดยไม่แปลงเป็นอาเรย์จะพบว่าไม่สามารถทำในสิ่งเดียวกันได้
liyu = [[1,2,3],[4,5,6]]
print(liyu[:][1]) # ได้ [4 5 6]
print(liyu[:,1]) # ได้ TypeError: list indices must be integers or slices, not tuple
print(liyu[:][1]) # ได้ [4 5 6]
print(liyu[:,1]) # ได้ TypeError: list indices must be integers or slices, not tuple
สรุปเป็นตารางเพื่อให้เห็นภาพชัด สมมุติว่าอาเรย์มี n แถว m หลัก
| แถว/หลัก | 0 | 1 | 2 | 3 | .. | m-1 |
| 0 | [0,0] | [0,1] | [0,2] | [0,3] | [0,..] | [0,m-1] |
| 1 | [1,0] | [1,1] | [1,2] | [1,3] | [1,..] | [1,m-1] |
| 2 | [2,0] | [2,1] | [2,2] | [2,3] | [2,..] | [2,m-1] |
| 3 | [3,0] | [3,1] | [3,2] | [3,3] | [3,..] | [3,m-1] |
| .. | [..,0] | [..,1] | [..,2] | [..,3] | [..,..] | [..,m-1] |
| n-1 | [n-1,0] | [n-1,1] | [n-1,2] | [n-1,3] | [n-1,..] | [n-1,m-1] |
สำหรับสามมิติซึ่งมีขนาด 3,3,3 อาจเขียนได้ดังนี้

การวางตัวเลขไว้หน้าและหลัง : เพื่อคัดเลือกอาเรย์เฉพาะในช่วงที่ต้องการก็ทำได้เช่นเดียวกับลิสต์
ตัวอย่างกรณีหนึ่งมิติ
aroi = np.array([13,14,15,16,17,18,19])
print(aroi[:3]) # ได้ [13 14 15]
print(aroi[3:5]) # ได้ [16 17]
print(aroi[5:]) # ได้ [18 19]
และเลขติดลบก็แสดงถึงสมาชิกที่ไล่จากท้าย โดย -1 คือสมาชิกตัวท้ายสุด
print(aroi[-1]) # ได้ 19
print(aroi[-3:-1]) # ได้ [17 18]
print(aroi[5:-1]) # ได้ [18]
หากมี : เพิ่มมาอีกตัวแล้ววางตัวเลขไว้ทางขวา : อีกจะเป็นการกำหนดระยะเว้นช่วง เช่นจะให้เว้นทีละสองก็ใส่ ::2 โดยตัวเลข ๒ ตัวแรกที่อยู่หน้า : อาจไม่ต้องใส่เลยก็ได้ และหากใส่เลขติดลบก็จะกลายเป็นการไล่ถอยหลังได้
print(aroi[1:4:2]) # ได้ [14 16]
print(aroi[1::2]) # ได้ [14 16 18]
print(aroi[:6:2]) # ได้ [13 15 17]
print(aroi[::2]) # ได้ [13 15 17 19]
print(aroi[::-1]) # ได้ [19 18 17 16 15 14 13]
จะเห็นว่าหากแค่ต้องการกลับลำดับสมาชิกในอาเรย์ทั้งหมดก็แค่ใส่ [::-1] ไปเท่านั้น เป็นการใช้ที่สะดวกมาก
กรณีสองมิติก็ใช้หลักการเดียวกัน ลองใช้กันดูได้
ตัวอย่าง
aroy = np.array([[13,14,15,16],
[17,18,19,20],
[21,22,23,24]])
print(aroy[1:2,2:3]) # ได้ [[19]]
print(aroy[0:2,1:3])# ได้
# [[14 15]
# [18 19]]
print(aroy[0,1:3]) # ได้ [14 15]
print(aroy[::2,2]) # ได้ [15 23]
print(aroy[::-1,::-1]) # ได้
# [[24 23 22 21]
# [20 19 18 17]
# [16 15 14 13]]
การเขียนทับข้อมูลในอาเรย์
เช่นเดียวกับลิสต์ อาเรย์ก็สามารถเขียนทับแก้ข้อมูลข้างในเมื่อไหร่ก็ได้ด้วยการใส่ค่าทับลงไป
aruy = np.array([[2,2,2],[2,2,2],[2,2,2]])
print(aruy)
aruy[1,1] = 3
print(aruy)
print(aruy)
aruy[1,1] = 3
print(aruy)
ได้
[[2 2 2]
[2 2 2]
[2 2 2]]
[[2 2 2]
[2 3 2]
[2 2 2]]
[2 2 2]
[2 2 2]]
[[2 2 2]
[2 3 2]
[2 2 2]]
แต่ที่สะดวกกว่านั้นก็คือหากอยากแก้ค่าของหลายตัวในแถวหรือหลักเดียวกันทีเดียวก็สามารถทำได้
aruy[1,:] = 4
print(aruy)
aruy[:,2] = 5
print(aruy)
aruy[:,:] = 6
print(aruy)
print(aruy)
aruy[:,2] = 5
print(aruy)
aruy[:,:] = 6
print(aruy)
ได้
[[2 2 2]
[4 4 4]
[2 2 2]]
[[2 2 5]
[4 4 5]
[2 2 5]]
[[6 6 6]
[6 6 6]
[6 6 6]]
[4 4 4]
[2 2 2]]
[[2 2 5]
[4 4 5]
[2 2 5]]
[[6 6 6]
[6 6 6]
[6 6 6]]
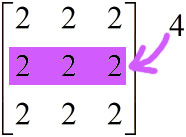
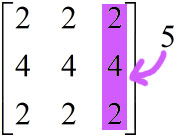
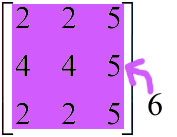
จะเห็นว่าถ้าเขียน [:,:] จะเป็นการอ้างถึงข้อมูลทั้งหมด และทุกตัวจะถูกเปลี่ยนให้มีค่าเท่ากันหมด
ลักษณะนี้เรียกว่าเป็นการกระจายค่า (broadcast) คือสามารถใช้เลขตัวเดียวมาแทนค่าเพื่อยัดใส่แทนสมาชิกหลายตัวในอาเรย์ได้ในทีเดียว
ที่น่าสนใจกว่านั้นหน่อยคือการกระจายค่าไม่ได้จำกัดอยู่แค่ตัวเลขเดี่ยว แต่ยังใช้กับอาเรย์ที่มีจำนวนมิติน้อยกว่าได้ด้วย เช่น
aruy[:,:] = np.array([7,8,9]) # หรือจะใช้ในรูปลิสต์ aruy[:,:] = [7,8,9] ก็ได้
print(aruy)
print(aruy)
ได้
[[7 8 9]
[7 8 9]
[7 8 9]]
[7 8 9]
[7 8 9]]
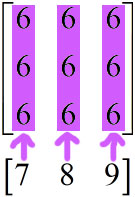
จะเห็นว่าค่า 7 8 9 ถูกกระจายเข้าไปในแต่ละแถวเหมือนกันหมด
แต่ขนาดของอาเรย์ที่จะมาแทนต้องเท่ากัน ไม่เช่นนั้นจะเกิดข้อผิดพลาด
aruy[:,:] = [7,8] # ได้ ValueError: could not broadcast input array from shape (2) into shape (3,3)
ในการกระจายนั้นจะกระจายตามแนวนอน ดังนั้นต่อให้มีจำนวนแถวแนวตั้งเท่ากับขนาดของอาเรย์ที่มาแทนก็ไม่ได้อยู่ดี
aruyo = np.array([[2,2,2],[2,2,2]])
aruyo[:,:] = [4,5] # ได้ ValueError: could not broadcast input array from shape (2) into shape (2,3)
aruyo[:,:] = [4,5] # ได้ ValueError: could not broadcast input array from shape (2) into shape (2,3)
เรื่องนี้อาจจะเข้าใจยากสักหน่อย เพื่อที่จะเข้าใจได้ควรจะลองใช้ดูเยอะๆเพื่อจะได้เข้าใจว่าทำแบบไหนแล้วจะเกิดผลอย่างไร
เรื่องของการเข้าถึงสมาชิกในอาเรย์ยังไม่ได้มีอยู่แค่นั้น มีวิธีการเข้าถึงที่ซับซ้อนกว่านี้แต่ก็ใช้ประโยชน์ได้ยืดหยุ่นมาก เรื่องนี้จะพูดถึงอีกทีในบทที่ ๑๙
การสร้างอาเรย์ด้วยฟังก์ชัน
นอกจากจะสร้างจากลิสต์แล้วอาเรย์ก็ยังสร้างจากฟังก์ชันต่างๆที่มีอยู่ในมอดูล numpy เองได้
ในที่นี้ขอแนะนำฟังก์ชันที่ใช้บ่อย ได้แก่
| np.arange | สร้างอาเรย์หนึ่งมิติที่มีเลขเรียงกัน |
| np.linspace | สร้างอาเรย์หนึ่งมิติตามจำนวนที่กำหนดโดยเว้นช่วงเท่าๆกัน |
| np.ones | สร้างอาเรย์ที่มีแต่เลข 1 ตามขนาดที่กำหนด |
| np.zeros | สร้างอาเรย์ที่มีแต่เลข 0 ตามขนาดที่กำหนด |
| np.full | สร้างอาเรย์ที่มีแต่เลขอะไรก็ได้เลขเดียวตามที่กำหนด โดยมีขนาดตามที่กำหนด |
| np.empty | สร้างอาเรย์เปล่าๆ ตามขนาดที่กำหนด |
| np.identity | สร้างอาเรย์ที่เป็นเมทริกซ์เอกลักษณ์ (เมทริกซ์สองมิติที่มีค่าเป็น 1 เมื่อพิกัดแนวตั้งและนอนเท่ากัน นอกนั้นเป็น 0) |
| np.eye | เหมือนกับ np.identity แต่ขนาดแนวตั้งและนอนไม่ต้องเท่ากันก็ได้ |
ในการสร้างอาเรย์ที่เป็นตัวเลขเรียงกันใช้ np.arange หรือ np.linspace
print(np.arange(10))
print(np.arange(1.5,8,2)) # อาร์กิวเมนต์ที่ใช้เหมือนกับ range แต่ไม่จำเป็นต้องเป็นจำนวนจริง
print(np.linspace(4, 7, 6)) # (จุดเริ่ม, จุดปลาย, จำนวน)
print(np.arange(1.5,8,2)) # อาร์กิวเมนต์ที่ใช้เหมือนกับ range แต่ไม่จำเป็นต้องเป็นจำนวนจริง
print(np.linspace(4, 7, 6)) # (จุดเริ่ม, จุดปลาย, จำนวน)
ผลลัพธ์
[0 1 2 3 4 5 6 7 8 9]
[ 1.5 3.5 5.5 7.5]
[ 4. 4.6 5.2 5.8 6.4 7. ]
[ 1.5 3.5 5.5 7.5]
[ 4. 4.6 5.2 5.8 6.4 7. ]
np.linspace ถ้าใส่คีย์เวิร์ด endpoint=0 ไปจะหมายความว่าไม่รวมเลขจุดปลายด้วย และผลที่ได้จะต่างไปจากเดิมเลย
print(np.linspace(1.,4.,6)) # ได้ [ 1. 1.6 2.2 2.8 3.4 4. ]
print(np.linspace(1.,4.,6,endpoint=0)) # ได้ [ 1. 1.5 2. 2.5 3. 3.5]
print(np.linspace(1.,4.,6,endpoint=0)) # ได้ [ 1. 1.5 2. 2.5 3. 3.5]
จะเห็นว่ากรณีที่รวมจุดปลายจะได้ว่า ระยะช่วง = (จุดเริ่ม-จุดสิ้นสุด)/(จำนวน-1)
แต่ถ้าไม่รวมจุดปลายด้วยจะได้ว่า ระยะช่วง = (จุดเริ่ม-จุดสิ้นสุด)/จำนวน
ทั้ง np.arange และ np.linspace ถูกใช้บ่อยๆเวลาวาดกราฟ จึงมีความสำคัญมาก
ในการสร้างอาเรย์ที่มีแต่ตัวเลข 0 หรือ 1 ล้วนๆใช้ np.ones และ np.zeros
print(np.ones(10))
print(np.ones([2,4])) # กรณีสร้างสองมิติขึ้นไปต้องใส่เป็นลิสต์หรือทูเพิล
print(np.zeros([2,5]))
print(np.ones([2,4])) # กรณีสร้างสองมิติขึ้นไปต้องใส่เป็นลิสต์หรือทูเพิล
print(np.zeros([2,5]))
ผลลัพธ์
[ 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]]
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
[[ 1. 1. 1. 1.]
[ 1. 1. 1. 1.]]
[[ 0. 0. 0. 0. 0.]
[ 0. 0. 0. 0. 0.]]
สำหรับค่าอื่นที่ไม่ใช่ 0 และ 1 ให้ใช้ np.full โดยใส่อาร์กิวเมนต์ตัวแรกเป็นมิติของอาเรย์ที่ต้องการ ส่วนตัวหลังเป็นค่าที่ต้องการซ้ำ
print(np.full(4,10))
print(np.full([2,2],5))
print(np.full([2,2],5))
ผลลัพธ์
[ 10. 10. 10. 10.]
[[ 5. 5.]
[ 5. 5.]]
[[ 5. 5.]
[ 5. 5.]]
นอกจากนี้ยังมี np.empty ซึ่งมีไว้สำหรับสร้างอาเรย์ตามขนาดที่ต้องการขึ้นมาโดยจะมีสมาชิกเป็นอะไรก็ไม่รู้ซึ่งเราไม่อาจควบคุมได้ เหมาะสำหรับเอาไว้สร้างอาเรย์เปล่าๆที่ไม่จำเป็นต้องสนว่ามีข้อมูลอะไรอยู่ก่อน สนแค่ขนาดเท่านั้น ข้อดีคือเร็วกว่า ones, zeros และ full เนื่องจากไม่จำเป็นต้องเตรียมค่าเริ่มต้น
print(np.empty([2,7]))
ผลลัพธ์
[[ 0.00000000e+000 0.00000000e+000 9.48788057e+150 2.67670692e+015
-1.13067367e+192 -3.37744342e+056 2.20318863e+228]
[ 6.21927996e+092 -2.62364069e+269 -7.83943927e+133 5.11600539e+305
1.44472795e+170 1.43897597e-314 9.73469813e-309]]
-1.13067367e+192 -3.37744342e+056 2.20318863e+228]
[ 6.21927996e+092 -2.62364069e+269 -7.83943927e+133 5.11600539e+305
1.44472795e+170 1.43897597e-314 9.73469813e-309]]
อาเรย์ของเมทริกซ์เอกลักษณ์สามารถสร้างโดย np.identity กับ np.eye
print(np.identity(3)) # ใส่อาร์กิวเมนต์ตัวเดียว สร้างได้แค่เมทริกซ์จตุรัสเท่านั้น
print(np.eye(2)) # ใส่อาร์กิวเมนต์เดียวจะได้ผลเหมือน np.identity
print(np.eye(2,5)) # ใส่สองอาร์กิวเมนต์ได้ แถวหรือหลักที่เกินจะเป็น 0 หมด
print(np.eye(2)) # ใส่อาร์กิวเมนต์เดียวจะได้ผลเหมือน np.identity
print(np.eye(2,5)) # ใส่สองอาร์กิวเมนต์ได้ แถวหรือหลักที่เกินจะเป็น 0 หมด
ผลลัพธ์
[[ 1. 0. 0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]
[[ 1. 0.]
[ 0. 1.]]
[[ 1. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]]
[ 0. 1. 0.]
[ 0. 0. 1.]]
[[ 1. 0.]
[ 0. 1.]]
[[ 1. 0. 0. 0. 0.]
[ 0. 1. 0. 0. 0.]]
คุณสมบัติการถ่ายทอดของอาเรย์
ขอทิ้งท้ายด้วยเรื่องสำคัญอีกอย่างหนึ่งเกี่ยวกับอาเรย์ที่ค่อนข้างสำคัญและจำเป็นต้องทำความเข้าใจไม่เช่นนั้นอาจก่อให้เกิดข้อผิดพลาดที่ไม่อาจค้นหาสาเหตุได้ นั่นคือการที่อาเรย์มีคุณสมบัติการถ่ายทอด
อาเรย์ที่ถูกสร้างขึ้นมาถือเป็นออบเจ็กต์อันหนึ่ง ถ้าหากมีตัวแปรมารับด้วย = มันก็จะแทนออบเจ็กต์อาเรย์นั้น และหากมีตัวแปรมารับต่อตัวแปรนั้นด้วย = อีก จะกลายเป็นว่าตัวแปรใหม่นั้นแทนออบเจ็กต์อาเรย์ตัวเดียวกัน หากมีการเปลี่ยนแปลงค่าภายในก็จะมีการเปลี่ยนแปลงไปตามกัน
ตัวอย่าง
aime = np.array([1,2,3,4,5])
aiment = aime
print(aiment) # ได้ [1 2 3 4 5]
print(aime) # ได้ [1 2 3 4 5]
aiment[1] = 6
print(aiment) # ได้ [1 6 3 4 5]
print(aime) # ได้ [1 6 3 4 5]
aiment = aime
print(aiment) # ได้ [1 2 3 4 5]
print(aime) # ได้ [1 2 3 4 5]
aiment[1] = 6
print(aiment) # ได้ [1 6 3 4 5]
print(aime) # ได้ [1 6 3 4 5]
จะเห็นว่า aiment = aime ทำให้ aiment กลายเป็นตัวแปรที่ใช้แทน aime พอมีการเปลี่ยนแปลงภายใน aiment (เช่นในที่นี้คือแก้ค่าสมาชิก [1] เป็น 6) aime ก็จะเปลี่ยนแปลงตาม
คุณสมบัติข้อนี้สามารถใช้กับลิสต์ได้ผลในทำนองเดียวกัน จึงดูไม่ใช่เรื่องอะไรแปลกใหม่
แต่นอกจากนี้แล้วอาเรย์ยังสามารถถ่ายทอดด้วยชิ้นส่วนที่ถูกตัดมาด้วย
aime = np.array([1,2,3,4,5])
aimez = aime[2:]
print(aimez) # ได้ [3 4 5]
print(aime) # ได้ [1 2 3 4 5]
aimez[1] = 8
print(aimez) # ได้ [3 8 5]
print(aime) # ได้ [1 2 3 8 5]
aimez = aime[2:]
print(aimez) # ได้ [3 4 5]
print(aime) # ได้ [1 2 3 4 5]
aimez[1] = 8
print(aimez) # ได้ [3 8 5]
print(aime) # ได้ [1 2 3 8 5]
จะเห็นว่า aimez = aime[2:] ทำให้ aimez กลายเป็นตัวแทนของส่วนตั้งแต่ตำแหน่ง [2] ของ aime จากนั้นพอมีการแก้ค่าภายใน aimez ค่าภายใน aime ก็จะถูกเปลี่ยนแปลงไปด้วย
คุณสมบัตินี้ไม่สามารถใช้กับลิสต์ได้ ลองเทียบดู
a = [1,2,3,4,5] # สร้าง a เป็นลิสต์ธรรมดา
avez = a[2:]
print(avez) # ได้ [3, 4, 5]
avez[1] = 8
print(avez) # ได้ [3, 8, 5]
print(a) # ได้ [1, 2, 3, 4, 5]
avez = a[2:]
print(avez) # ได้ [3, 4, 5]
avez[1] = 8
print(avez) # ได้ [3, 8, 5]
print(a) # ได้ [1, 2, 3, 4, 5]
จะเห็นว่าในที่นี้ avez แค่มารับเอาค่าในช่วงตั้งแต่ตำแหน่ง [2] ของ a แต่ไม่ได้เป็นตัวแทน ดังนั้นพอมีการแก้ค่าใน avez จึงไม่ทำให้ค่าใน a เปลี่ยนแปลงตาม
จากตรงนี้จะเห็นได้ถึงข้อแตกต่างระหว่างอาเรย์กับลิสต์อีกอย่าง
คุณสมบัติตรงนี้อาจเป็นได้ทั้งประโยชน์และโทษ
ที่อาจเป็นโทษได้นั้นก็เพราะว่าหากใครรู้เท่าไม่ถึงการแค่อยากจะได้อาเรย์ใหม่ ที่เอาค่าของอาเรย์เก่ามาใช้ แต่กลับกลายเป็นว่าเป็นการสร้างอาเรย์ที่เป็นตัวแทนของส่วนหนึ่งของอาเรย์ เก่าขึ้นมา แบบนี้พอแก้อะไรในอาเรย์ใหม่ อาเรย์เก่าก็จะถูกเปลี่ยนไปด้วย ซึ่งเป็นเหตุการณ์ที่อันตราย
เพื่อที่จะหลีกเลี่ยงเรื่องแบบนั้น จำเป็นจะต้องใช้เมธอด copy() เวลาที่ต้องการสร้างอาเรย์ใหม่จากอาเรย์เก่า แบบนี้จะเป็นการสร้างอาเรย์ใหม่ขึ้นมาโดยไม่เกี่ยวกับตัวเก่าอีกเลย
ตัวอย่าง
aime = np.array([1,2,3,4,5])
aimons = aime[2:].copy()
print(aimons) # ได้ [3 4 5]
print(aime) # ได้ [1 2 3 4 5]
aimons[1] = 8
print(aimons) # ได้ [3 8 5]
print(aime) # ได้ [1 2 3 4 5]
aimons = aime[2:].copy()
print(aimons) # ได้ [3 4 5]
print(aime) # ได้ [1 2 3 4 5]
aimons[1] = 8
print(aimons) # ได้ [3 8 5]
print(aime) # ได้ [1 2 3 4 5]
จะเห็นว่าเมื่อเติม .copy() ต่อท้ายลงไปตอนสร้างอาเรย์ aimons ขึ้นมาจะทำให้อาเรย์นี้กลายเป็นอาเรย์ใหม่ที่ไม่มีความเกี่ยวข้องอะไรกับ aime ทีนี้แม้ว่าจะมีการเปลี่ยนแปลงค่าภายในไปก็จะไม่กระทบต่ออาเรย์เก่า
copy นี้นอกจากจะเขียนในรูปเมธอดต่อท้ายแบบนี้ยังอาจเขียนในรูปฟังก์ชัน เป็น np.copy() ได้ด้วย
สรุปข้อแตกต่างระหว่างอาเรย์กับลิสต์
- อาเรย์จะต้องประกอบด้วยข้อมูลเพียงชนิดเดียวเท่านั้น
- อาเรย์ต้องมีจำนวนข้อมูลในแต่ละแถวเท่ากันหมด
- อาเรย์สามารถคำนวณทางคณิตศาสตร์ได้โดยตรง
- อาเรย์คำนวณได้เร็วกว่า
- อาเรย์มีวิธีการเข้าถึงข้อมูลภายในได้ยืดหยุ่นกว่า
- อาเรย์มีคุณสมบัติการถ่ายทอดภายในชิ้นส่วนประกอบ
อ้างอิง
http://www.kamishima.net/mlmpyja/nbayes1/ndarray.html
http://www.turbare.net/transl/scipy-lecture-notes/intro/numpy/index.html
http://rest-term.com/archives/2999
http://ism1000ch.hatenablog.com/entry/2014/01/09/223330
http://hennohito.cocolog-nifty.com/blog/2014/08/pythonpylabnump.html
http://www.turbare.net/transl/scipy-lecture-notes/intro/numpy/index.html
http://rest-term.com/archives/2999
http://ism1000ch.hatenablog.com/entry/2014/01/09/223330
http://hennohito.cocolog-nifty.com/blog/2014/08/pythonpylabnump.html