numpy & matplotlib เบื้องต้น บทที่ ๒๓: อาเรย์สามมิติ
เขียนเมื่อ 2016/06/12 01:51
แก้ไขล่าสุด 2021/09/28 16:42
ในบทที่ผ่านๆมาเรามักจะพูดถึงอาเรย์หนึ่งหรือสองมิติเป็นหลัก แต่แทบไม่ได้พูดถึงมิติที่เหนือขึ้นมาเลย เนื่องจากว่ายิ่งมิติสูงก็ยิ่งเข้าใจยาก แต่หากใครอ่านมาจนถึงตรงนี้คิดว่าน่าจะได้ทำความเข้าใจและคุ้นเคยกับ numpy มามากพอสมควรแล้ว ในบทนี้จะเริ่มมาพูดถึงสามมิติ
ความจริงแล้วหลักการของสามมิติก็เหมือนสองมิติ เพียงแต่พอมิติเพิ่มขึ้นก็อาจทำให้ต้องอาศัยพลังในการมองภาพที่มากกว่าเดิม
สามมิตินั้นยังอยู่ในระดับที่คนทั่วไปสามารถมองภาพและเข้าใจได้อยู่ แต่หากสูงกว่าสามมิติขึ้นไปจะมีความเป็นนามธรรมสูงมากและคงจะไม่ได้กล่าวถึง ในนี้
การสร้างอาเรย์สามมิติจากการนำอาเรย์หนึ่งหรือสองมิติมาต่อกัน
ในบทที่ ๔ ได้พูดถึงการนำเอาอาเรย์มาต่อรวมกันไปแล้ว แต่ไม่ได้พูดถึงอาเรย์ที่เป็นสามมิติ คราวนี้จะลองมาดูกันว่าถ้าใช้กับสามมิติจะเป็นอย่างไร
ฟังก์ชัน np.stack มีไว้สำหรับทำการต่ออาเรย์ ซึ่งหากใช้กับอาเรย์หนึ่งมิติก็จะได้อาเรย์สองมิติออกมา แต่หากใช้กับอาเรย์สองมิติก็จะได้อาเรย์สามมิติ
อาเรย์ที่จะต่อกันนั้นจะต้องมีขนาดเท่ากัน โดยจะเป็นการเอามาเรียงต่อกันในแนวลึก
ตัวอย่าง
หากต้องการเปลี่ยนแกนที่หันหลังจากการประกอบกันก็ทำได้โดยใส่คีย์เวิร์ด axis ผลที่ได้จะเหมือนกับเรานำอาเรย์มาหมุนหันเปลี่ยนข้างแล้วค่อยประกบกัน
กรณี axis=1
กรณีที่ axis=2 จะมีค่าเหมือนกับการใช้ฟังก์ชัน np.dstack
ฟังก์ชัน np.dstack ยังสามารถใช้สร้างอาเรย์สามมิติขึ้นจากอาเรย์หนึ่งมิติได้ด้วย เพียงแต่ว่าจำนวนแถวในแนวลึกก็จะมีแค่แถวเดียวจึงดูแล้วไม่ต่างจากสองมิติ
การนำอาเรย์สามมิติมาต่อกัน
ฟังก์ชัน np.hstack, np.vstack และ np.dstack เมื่อนำมาใช้กับอาเรย์สามมิติจะได้ผลเป็นอาเรย์สามมิติเหมือนกัน เพียงแต่ว่าผลที่ได้จะต่างกัน เป็นการนำอาเรย์มาต่อกันในแนวต่างๆ
ตัวอย่าง
ส่วนฟังก์ชัน np.stack นั้นหากใช้กับอาเรย์สามมิติก็จะได้ผลเป็นอาเรย์สี่มิติ ซึ่งไม่สามารถวาดให้เห็นภาพ ณ ที่นี้ได้
การแยกอาเรย์สามมิติ
อาเรย์สามมิติสามารถแยกได้ด้วยคำสั่ง np.split, np.hsplit, np.vsplit และ np.dsplit
np.split จะทำการแยกอาเรย์ออกเป็นลิสต์ของอาเรย์หลายอันตามจำนวนที่กำหนด
กรณีที่ไม่กำหนด axis จะถือว่า axis=0 เป็นการแยกตามแนวตอนลึก ผลที่ได้จะเหมือนกับใช้ np.vsplit
ตัวอย่าง
ถ้า axis=1 จะเป็นการแยกตามแนวตั้ง ผลที่ได้เหมือนการใช้ np.hsplit
ถ้า axis=2 จะเป็นการแยกตามแนวหลักซ้ายขวา ผลที่ได้เหมือนการใช้ np.dsplit
การกระจายค่าในสามมิติ
เมื่อนำอาเรย์สามมิติมาคำนวณกับอาเรย์สามมิติเองจะเป็นการเอาสมาชิกแต่ละตัวมาคำนวณกันเป็นคู่ๆ อันนี้ไม่มีอะไรเข้าใจยาก
แต่หากนำอาเรย์สามมิติมาคำนวณกับอาเรย์หนึ่งหรือสองมิติจะเป็นไปตามคุณสมบัติการกระจายค่า
จะเห็นได้ว่าเวลาที่จะนำมาคำนวณกันขนาดของมิติตัวหลังสุดจะต้องเท่ากัน เช่นขนาด (2,4,3) ต้องทำกับ (4,3) หรือ 3 แต่จะทำกับ (3,4) หรือ 4 ไม่ได้
ตัวอย่าง
หรือ (4,1) ก็ใช้ได้เช่นกัน เพราะจะมีการกระจายตามแนวแกนหลังสุดกลายเป็น (4,3) แล้วจึงไปคำนวณกับ (2,4,3) ได้
แล้วถ้าต้องการเปลี่ยนแนวในการคำนวณ เช่นเอาอาเรย์ขนาด 4 มาคำนวณกับอาเรย์ขนาด (2,4,3) กรณีแบบนี้จำเป็นจะต้องนำอาเรย์มาหมุนพลิกก่อน ถ้าอาเรย์กลายเป็นขนาด (4,1) ก็จะคำนวณกันได้
การที่อยู่ดีๆจะเพิ่มมิติแล้วหมุนพลิกด้านทันที วิธีที่ง่ายที่สุดคือใช้ None หรือ np.newaxis (ดังที่กล่าวไว้ในบทที่ ๔)
อาเรย์สองมิติด้วยกันเองหากเอาอันหนึ่งมาพลิกให้ไปอยู่ในสามมิติก็สามารถคำนวณออกมาเป็นสามมิติได้เช่นกัน เช่น

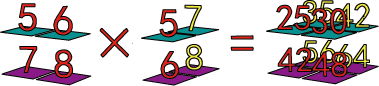
หรือหนึ่งมิติก็พลิกแล้วคำนวณกันออกมาเป็นสามมิติได้เช่นกัน
การจัดการข้อมูลภายในอาเรย์สามมิติ
ฟังก์ชันหรือเมธอดสำหรับวิเคราะห์ข้อมูล จำพวก max min sum mean ฯลฯ ปกติแล้วหากไม่ระบุคีย์เวิร์ด axis จะเป็นการคิดข้อมูลทั้งหมดโดยยุบรวมกันเป็นมิติเดียว ผลลัพธ์มีเพียงหนึ่ง แต่หากระบุแกนก็จะเป็นการคิดผลลัพธ์โดยแบ่งตามแกนที่ระบุ ดังนั้นเมื่อใช้จะต้องระบุแกนให้ถูก ผลที่ได้จะมีมิติลดลงหนึ่งมิติเพราะเอาข้อมูลตลอดทั้งมิติมารวบยอด
ขอยกตัวอย่างดูด้วยฟังก์ชัน min
ได้
รูปนี้เป็นการใช้ฟังก์ชัน mean
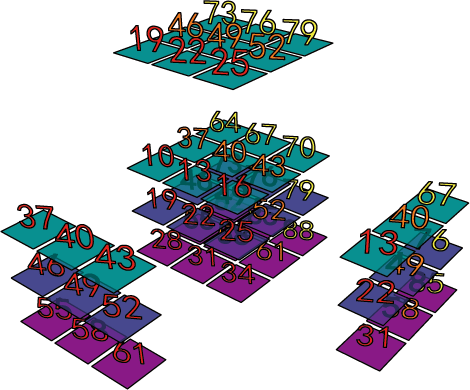
ความจริงแล้วหลักการของสามมิติก็เหมือนสองมิติ เพียงแต่พอมิติเพิ่มขึ้นก็อาจทำให้ต้องอาศัยพลังในการมองภาพที่มากกว่าเดิม
สามมิตินั้นยังอยู่ในระดับที่คนทั่วไปสามารถมองภาพและเข้าใจได้อยู่ แต่หากสูงกว่าสามมิติขึ้นไปจะมีความเป็นนามธรรมสูงมากและคงจะไม่ได้กล่าวถึง ในนี้
การสร้างอาเรย์สามมิติจากการนำอาเรย์หนึ่งหรือสองมิติมาต่อกัน
ในบทที่ ๔ ได้พูดถึงการนำเอาอาเรย์มาต่อรวมกันไปแล้ว แต่ไม่ได้พูดถึงอาเรย์ที่เป็นสามมิติ คราวนี้จะลองมาดูกันว่าถ้าใช้กับสามมิติจะเป็นอย่างไร
ฟังก์ชัน np.stack มีไว้สำหรับทำการต่ออาเรย์ ซึ่งหากใช้กับอาเรย์หนึ่งมิติก็จะได้อาเรย์สองมิติออกมา แต่หากใช้กับอาเรย์สองมิติก็จะได้อาเรย์สามมิติ
อาเรย์ที่จะต่อกันนั้นจะต้องมีขนาดเท่ากัน โดยจะเป็นการเอามาเรียงต่อกันในแนวลึก
ตัวอย่าง
a1 = np.ones([3,4])*2
a2 = np.ones([3,4])*3
# ขอใช้ภาพสามมิติแสดงแทนอาเรย์เพื่อให้เห็นภาพชัด
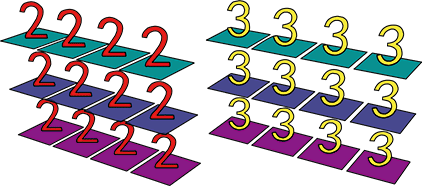
print(np.stack((a1,a2)))
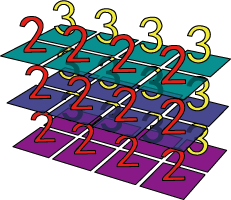
a2 = np.ones([3,4])*3
# ขอใช้ภาพสามมิติแสดงแทนอาเรย์เพื่อให้เห็นภาพชัด

print(np.stack((a1,a2)))

หากต้องการเปลี่ยนแกนที่หันหลังจากการประกอบกันก็ทำได้โดยใส่คีย์เวิร์ด axis ผลที่ได้จะเหมือนกับเรานำอาเรย์มาหมุนหันเปลี่ยนข้างแล้วค่อยประกบกัน
กรณี axis=1
print(np.stack((a1,a2),axis=1))


กรณีที่ axis=2 จะมีค่าเหมือนกับการใช้ฟังก์ชัน np.dstack
print(np.stack((a1,a2),axis=2)) # หรือ print(np.dstack((a1,a2)))


ฟังก์ชัน np.dstack ยังสามารถใช้สร้างอาเรย์สามมิติขึ้นจากอาเรย์หนึ่งมิติได้ด้วย เพียงแต่ว่าจำนวนแถวในแนวลึกก็จะมีแค่แถวเดียวจึงดูแล้วไม่ต่างจากสองมิติ
a1 = np.ones(3)*4
a2 = np.ones(3)*5
print(np.dstack((a1,a2)))

a2 = np.ones(3)*5
print(np.dstack((a1,a2)))

การนำอาเรย์สามมิติมาต่อกัน
ฟังก์ชัน np.hstack, np.vstack และ np.dstack เมื่อนำมาใช้กับอาเรย์สามมิติจะได้ผลเป็นอาเรย์สามมิติเหมือนกัน เพียงแต่ว่าผลที่ได้จะต่างกัน เป็นการนำอาเรย์มาต่อกันในแนวต่างๆ
ตัวอย่าง
a1 = np.ones([2,2,2])*6
a2 = np.ones([2,2,2])*7
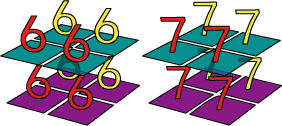
print(np.hstack((a1,a2)))
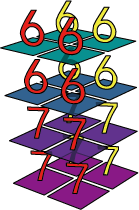
print(np.vstack((a1,a2)))
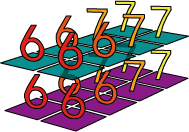
print(np.dstack((a1,a2)))
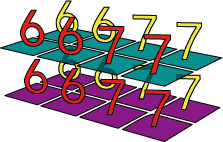
a2 = np.ones([2,2,2])*7

print(np.hstack((a1,a2)))

print(np.vstack((a1,a2)))

print(np.dstack((a1,a2)))

ส่วนฟังก์ชัน np.stack นั้นหากใช้กับอาเรย์สามมิติก็จะได้ผลเป็นอาเรย์สี่มิติ ซึ่งไม่สามารถวาดให้เห็นภาพ ณ ที่นี้ได้
การแยกอาเรย์สามมิติ
อาเรย์สามมิติสามารถแยกได้ด้วยคำสั่ง np.split, np.hsplit, np.vsplit และ np.dsplit
np.split จะทำการแยกอาเรย์ออกเป็นลิสต์ของอาเรย์หลายอันตามจำนวนที่กำหนด
กรณีที่ไม่กำหนด axis จะถือว่า axis=0 เป็นการแยกตามแนวตอนลึก ผลที่ได้จะเหมือนกับใช้ np.vsplit
ตัวอย่าง
aa = np.arange(24).reshape(2,3,4)
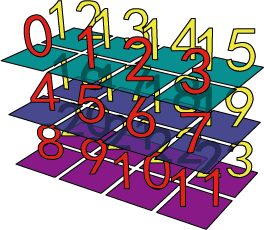
print(np.split(aa,2)) # หรือ print(np.vsplit(aa,2))
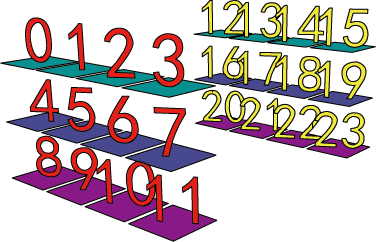

print(np.split(aa,2)) # หรือ print(np.vsplit(aa,2))

ถ้า axis=1 จะเป็นการแยกตามแนวตั้ง ผลที่ได้เหมือนการใช้ np.hsplit
print(np.split(aa,3,axis=1)) # หรือ print(np.hsplit(aa,2))
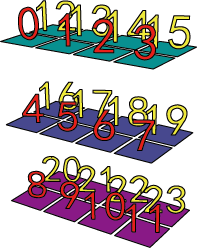

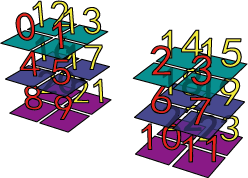
ถ้า axis=2 จะเป็นการแยกตามแนวหลักซ้ายขวา ผลที่ได้เหมือนการใช้ np.dsplit
print(np.dsplit(aa,2)) # หรือ print(np.dsplit(aa,2))

การกระจายค่าในสามมิติ
เมื่อนำอาเรย์สามมิติมาคำนวณกับอาเรย์สามมิติเองจะเป็นการเอาสมาชิกแต่ละตัวมาคำนวณกันเป็นคู่ๆ อันนี้ไม่มีอะไรเข้าใจยาก
แต่หากนำอาเรย์สามมิติมาคำนวณกับอาเรย์หนึ่งหรือสองมิติจะเป็นไปตามคุณสมบัติการกระจายค่า
จะเห็นได้ว่าเวลาที่จะนำมาคำนวณกันขนาดของมิติตัวหลังสุดจะต้องเท่ากัน เช่นขนาด (2,4,3) ต้องทำกับ (4,3) หรือ 3 แต่จะทำกับ (3,4) หรือ 4 ไม่ได้
ตัวอย่าง
a1 = np.ones([2,4,3])
a1[1] = 3
a2 = np.arange(1,4)
print(a1*a2)
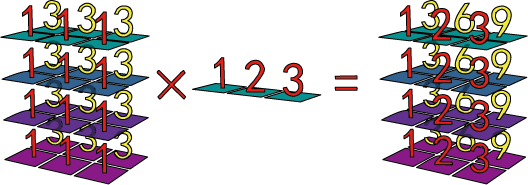
a1 = np.ones([2,4,3])*4
a1[1] = 5
a2 = np.arange(1,13).reshape(4,3)
print(a1*a2)
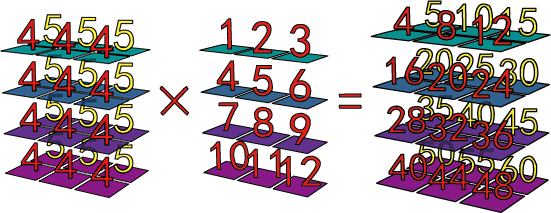
a1[1] = 3
a2 = np.arange(1,4)
print(a1*a2)
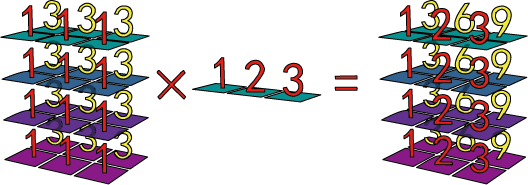
a1 = np.ones([2,4,3])*4
a1[1] = 5
a2 = np.arange(1,13).reshape(4,3)
print(a1*a2)
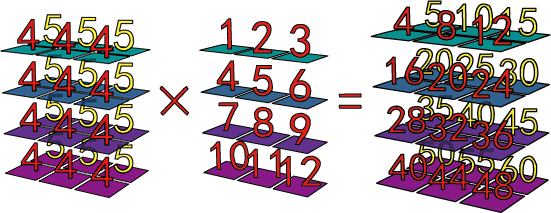
หรือ (4,1) ก็ใช้ได้เช่นกัน เพราะจะมีการกระจายตามแนวแกนหลังสุดกลายเป็น (4,3) แล้วจึงไปคำนวณกับ (2,4,3) ได้
แล้วถ้าต้องการเปลี่ยนแนวในการคำนวณ เช่นเอาอาเรย์ขนาด 4 มาคำนวณกับอาเรย์ขนาด (2,4,3) กรณีแบบนี้จำเป็นจะต้องนำอาเรย์มาหมุนพลิกก่อน ถ้าอาเรย์กลายเป็นขนาด (4,1) ก็จะคำนวณกันได้
การที่อยู่ดีๆจะเพิ่มมิติแล้วหมุนพลิกด้านทันที วิธีที่ง่ายที่สุดคือใช้ None หรือ np.newaxis (ดังที่กล่าวไว้ในบทที่ ๔)
a1 = np.ones([2,4,3])*4
a1[1] = 5
a2 = np.arange(1,5)[:,np.newaxis] # เท่านี้ก็กลายเป็นอาเรย์ (4,1)
print(a1*a2)
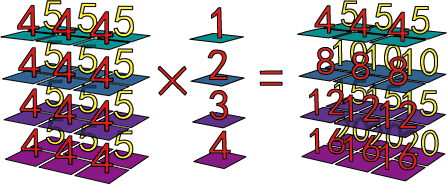
a1[1] = 5
a2 = np.arange(1,5)[:,np.newaxis] # เท่านี้ก็กลายเป็นอาเรย์ (4,1)
print(a1*a2)
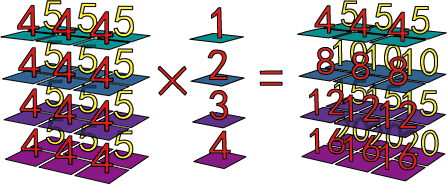
อาเรย์สองมิติด้วยกันเองหากเอาอันหนึ่งมาพลิกให้ไปอยู่ในสามมิติก็สามารถคำนวณออกมาเป็นสามมิติได้เช่นกัน เช่น

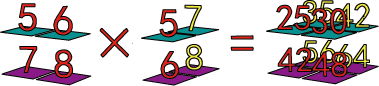
หรือหนึ่งมิติก็พลิกแล้วคำนวณกันออกมาเป็นสามมิติได้เช่นกัน
การจัดการข้อมูลภายในอาเรย์สามมิติ
ฟังก์ชันหรือเมธอดสำหรับวิเคราะห์ข้อมูล จำพวก max min sum mean ฯลฯ ปกติแล้วหากไม่ระบุคีย์เวิร์ด axis จะเป็นการคิดข้อมูลทั้งหมดโดยยุบรวมกันเป็นมิติเดียว ผลลัพธ์มีเพียงหนึ่ง แต่หากระบุแกนก็จะเป็นการคิดผลลัพธ์โดยแบ่งตามแกนที่ระบุ ดังนั้นเมื่อใช้จะต้องระบุแกนให้ถูก ผลที่ได้จะมีมิติลดลงหนึ่งมิติเพราะเอาข้อมูลตลอดทั้งมิติมารวบยอด
ขอยกตัวอย่างดูด้วยฟังก์ชัน min
a = np.arange(10,91,3).reshape(3,3,3)
print(a)
print(a.min(axis=0))
print(a.min(axis=1))
print(a.min(axis=2))
print(a)
print(a.min(axis=0))
print(a.min(axis=1))
print(a.min(axis=2))
ได้
[[[10 13 16]
[19 22 25]
[28 31 34]]
[[37 40 43]
[46 49 52]
[55 58 61]]
[[64 67 70]
[73 76 79]
[82 85 88]]]
[[10 13 16]
[19 22 25]
[28 31 34]]
[[10 13 16]
[37 40 43]
[64 67 70]]
[[10 19 28]
[37 46 55]
[64 73 82]]
[19 22 25]
[28 31 34]]
[[37 40 43]
[46 49 52]
[55 58 61]]
[[64 67 70]
[73 76 79]
[82 85 88]]]
[[10 13 16]
[19 22 25]
[28 31 34]]
[[10 13 16]
[37 40 43]
[64 67 70]]
[[10 19 28]
[37 46 55]
[64 73 82]]
รูปนี้เป็นการใช้ฟังก์ชัน mean
