numpy & matplotlib เบื้องต้น บทที่ ๔: การตัดแต่งแก้ไขอาเรย์
เขียนเมื่อ 2016/06/11 12:07
แก้ไขล่าสุด 2021/09/28 16:42
อาเรย์นั้นนอกจากจะมีความยืดหยุ่นในการสร้างและนำมาคำนวณแล้ว ก็ยังมีความยืดหยุ่นในการเปลี่ยนรูปด้วย เราสามารถสร้างอาเรย์หนึ่งขึ้นจากอาเรย์ที่มีอยู่ก่อนด้วยการนำมาประกอบกัน ไม่ยาก
การขึ้นรูปใหม่
เราสามารถนำสมาชิกในอาเรย์มาจัดเรียงใหม่ได้ด้วยการใช้เมธอด reshape โดยกำหนดรูปร่างใหม่ของอาเรย์
reshape เป็นเมธอดที่จะทำการคืนอาเรย์ใหม่ที่มีขนาดมิติเท่ากับที่กำหนด
ผลลัพธ์
รูปร่างใหม่ของอาเรย์จำเป็นจะต้องรองรับสมาชิกเท่ากับจำนวนสมาชิกในอาเรย์เดิม ไม่เช่นนั้นจะเกิดข้อผิดพลาด
มีเมธอดอีกตัวที่คล้ายๆกันคือ resize ซึ่งมีหน้าที่เปลี่ยนแปลงโครงสร้างของอาเรย์ที่นำมากระทำให้เป็นไปตามที่กำหนด
resize จะไม่คืนค่าอะไรกลับมา แต่จะเป็นการเปลี่ยนรูปของอาเรย์นั้นไปเลย ต่างจาก reshape ซึ่งแค่ไว้คืนค่ากลับมาโดยไม่ได้เปลี่ยนตัวอาเรย์นั้นเอง
arr.resize(n,m) เทียบเท่ากับ arr = arr.reshape(n,m)
ตัวอย่าง
ผลลัพธ์
การยุบให้เหลือมิติเดียว
บางครั้งเราอาจมีอาเรย์สองมิติขึ้นไปอยู่แต่ต้องการยุบให้เหลือมิติเดียวเพื่อความสะดวกในการใช้งานบางอย่าง
กรณีแบบนี้จะใช้คำสั่ง reshape แล้วใส่ค่าเป็นจำนวนสมาชิกของอาเรย์ก็ได้ แต่ว่ามีคำสั่งสำหรับการนี้โดยเฉพาะซึ่งใช้งานได้ง่ายกว่านั้น นั่นคือ flatten กับ ravel
ตัวอย่างการใช้ flatten
ผลลัพธ์
ตัวอย่างนี้จะใช้ ravel ก็ได้ผลแบบเดียวกัน
ข้อแตกต่างของ ravel กับ flatten ก็คือ flatten จะทำการคัดลอกสมาชิกในอาเรย์มา ในขณะที่ ravel จะแค่คืนค่ามุมมองที่อ้างอิงถึง
ลองยกตัวอย่างให้เห็นความแตกต่าง
ผลลัพธ์
ผลลัพธ์
จะเห็นว่า xfla ใช้ flatten ซึ่งเป็นการคัดลอกค่าแล้วสร้างข้อมูลขึ้นใหม่ ดังนั้นพอมีการแก้ไขค่าใน xfla ก็ไม่ได้กระทบอะไรกับ x
แต่ว่า xra นั้นใช้ ravel เป็นแค่การดึงมุมมองมาใช้ไม่ได้สร้างข้อมูลใหม่ ยังใช้หน่วยความจำเดียวกันกับ x อยู่ ดังนั้นพอมีการแก้ไขค่าใน xra แล้ว ค่าใน x ก็จะเปลี่ยนตาม
ravel จะเขียนในรูปฟังก์ชันหรือเมธอดก็ได้ เช่น np.ravel(x) มีค่าเท่ากับ x.ravel() แต่ไม่สามารถเขียน np.flatten(x) ได้ ต้องเขียน x.flatten() เท่านั้น
การสลับแกนของอาเรย์
สำหรับอาเรย์สองมิติสามารถสลับแกนได้ด้วยคำสั่ง transpose จะเขียนในรูปเมธอดหรือฟังก์ชันก็ได้
ผลลัพธ์
นอกจาก นี้ยังอาจหาค่าทรานสโพสได้อย่างง่ายๆโดยเขียนต่อท้ายอาเรย์ด้วย .T ก็ได้ ข้อแตกต่างคือ .T ไม่ใช่เมธอด ไม่ต้องมีวงเล็บ () ต่อท้าย
สำหรับมิติที่สูงขึ้นไปใช้เมธอด swapaxes โดยใส่เลขของมิติ (แกน) ทั้งสองที่ต้องการสลับลงไป โดยมิติแรกนับเป็น 0
ถ้าใช้กับสองมิติ ใส่เป็น (0,1) จะได้ผลเหมือนกับ transpose
ผลลัพธ์
swapaxes จะเขียนในรูปฟังก์ชันก็ได้เช่นกัน คือ np.swapaxes(x,0,1)
การเพิ่มมิติขึ้นมา
ปกติแล้วคำสั่ง transpose หรือ T จะใช้กับที่เป็นสองอาเรย์สองมิติ หากใช้กับอาเรย์ที่เป็นหนึ่งมิติจะไม่มีการเปลี่ยนแปลง
หากต้องการจะนำอาเรย์หนึ่งมิติมาสลับเปลี่ยนการจับวางสลับแถวในสองมิติเราจะ เป็นต้องทำการเพิ่มมิตินั้นสามารถทำได้ด้วยวิธีการที่อาจจะดูแปลกสักหน่อย นั่นคือเติม [None] ไว้ข้างท้ายอาเรย์ มิติก็จะเพิ่มขึ้นมาทันที
เช่น
แบบนี้ก็จะได้อาเรย์สองมิติ แม้ว่าแกนตั้งจะมีแค่แถวเดียวก็ตาม
เท่านี้ก็สามารถนำมาทรานสโพสได้
นอกจากนี้เราอาจสลับแกนได้ทันทีด้วยการเติม :, ไว้ด้านหน้า None
หากใช้กับอาเรย์สองมิติก็จะกลายเป็นอาเรย์สามมิติได้
นั่นหมายความว่าจากอาเรย์หนึ่งมิติหากใส่ [None] ๒ ครั้งก็จะกลายเป็นสามมิติได้
เราสามารถใช้วิธีนี้เพื่อสลับแกนของอาเรย์สองมิติไปอยู่ในมิติที่สามได้
นอกจากนี้แล้วยังมีวิธีการอีกอย่างที่ให้ผลเหมือนกัน คือใช้ฟังก์ชัน np.expand_dims
แต่เนื่องจากเขียนยาวกว่าจึงดูเหมือนจะไม่เป็นที่นิยมนัก ใช้ [None] ง่ายกว่า แม้จะดูแล้วอาจเข้าใจยากสักหน่อยก็ตาม
เพื่อให้เข้าใจการทำงานของ None มากขึ้นอาจลองดูตัวอย่างนี้
จะเห็นว่า None เข้าไปแทนตำแหน่งแกนไหนตรงนั้นจะมีขนาดเป็น 1 ส่วนแกนที่เหลือก็จะได้มิติตามอาเรย์เดิม
ที่จริงแล้ว None ซึ่งถูกใช้ในกรณีนี้มักถูกใช้เป็น np.newaxis มากกว่า เพราะดูแล้วเหมือนเข้าใจได้ง่าย แต่ np.newaxis ก็เป็นเหมือนตัวแปรตัวแทนของ None
ดังนั้นจึงไม่มีความจำเป็นต้องใช้ np.newaxis จริงๆ แต่อย่างไรก็ตามก็แล้วแต่คน หากเห็นว่า None มันดูไม่สวย ดูแล้วไม่สื่อความหมาย ก็อาจใช้ np.newaxis ก็ได้
การนำอาเรย์มาต่อเข้าด้วยกัน
numpy มีคำสั่งที่สะดวกที่ใช้ในการเอาอาเรย์มาต่อกัน ได้แก่
การต่อกันของอาเรย์นั้นในบางกรณีจะทำให้มิติเพิ่มขึ้นมาอีกหนึ่งได้ แต่บางทีก็อาจไม่เพิ่ม แล้วแต่กรณีและฟังก์ชันที่ใช้
ที่จริงแล้วมีอีกฟังก์ชันหนึ่งซึ่งใช้รวมอาเรย์ให้เป็นสามมิติ นั่นคือ np.dstack แต่สำหรับกรณีที่ได้สามมิตินั้นจะค่อนข้างซับซ้อน จะยังขอไม่พูดถึงตอนนี้มากแต่ยกไปเน้นในบทที่ ๒๓
ถ้าใช้กับอาเรย์หนึ่งมิติ
- hstack จะเป็นการเอาอาเรย์มาต่อกัน เท่ากับ np.concatenate( (a, b),axis=0)
- vstack จะเป็นการรวมกันให้เป็นหลายแถว เท่ากับ np.stack( (a,b),axis=0)
ตัวอย่าง
ถ้าใช้กับอาเรย์สองมิติ
- hstack จะเป็นการรวมกันตามแนวนอน เท่ากับ np.concatenate( (a, b),axis=1)
- vstack จะเป็นการรวมกันตามแนวตั้ง เท่ากับ np.concatenate( (a, b),axis=0)
- stack จะเป็นการรวมกันในแนวมิติที่สาม
ตัวอย่าง
การแยกอาเรย์
หากต้องการแยกอาเรย์ออกเป็นส่วนๆไว้ในลิสต์ มีฟังก์ชันกลุ่มหนึ่งที่สามารถใช้ได้
นอกจากนี้ก็มี dsplit ซึ่งเอาไว้แยกตามมิติที่สาม
ตัวอย่าง
การจะใช้ฟังก์ชันแยกอาเรย์ได้นั้นจำนวนส่วนที่แบ่งจะต้องหารลงตัวกับจำนวนแถวหรือหลัก
การซ้ำอาเรย์
หากต้องการนำอาเรย์ตัวเดิมมาต่อกันหลายๆครั้งสามารถใช้ฟังก์ชัน np.tile
การใช้คือ np.tile(อาเรย์, จำนวนที่ซ้ำ)
ตัวอย่าง
การใส่อาร์กิวเมนต์ตัวหลังเป็นแค่ตัวเลขเดี่ยวจะเป็นการซ้ำในแนวแกนสุดท้าย แต่ถ้าต้องการให้ซ้ำในแนวอื่นต้องเปลี่ยนเป็นใส่ทูเพิล
ได้
ได้
อีกตัวหนึ่งที่มีไว้สำหรับซ้ำอาเรย์เหมือนกันคือ np.repeat แต่จะต่างกันเล็กน้อยคือ repeat จะนำเอาอาเรย์มายุบเหลือมิติเดียว จากนั้นทำซ้ำโดยเอาตัวเดิมอยู่ติดกัน
ตัวอย่าง
ได้
จะเห็นว่าแม้จะใช้อาเรย์สองมิติ แต่ก็ถูกยุบรวมเหลือมิติเดียว
หากต้องการให้คิดมิติด้วยก็เพิ่มคีย์เวิร์ด axis ลงไป
ได้
การกลับลำดับอาเรย์
numpy ไม่มีฟังก์ชันสำหรับกลับลำดับของอาเรย์โดยเฉพาะ แต่สามารถกลับลำดับของอาเรย์ได้โดยการเขียนแบบนี้ ar[::-1] แบบนี้จะเป็นการกลับลำดับของอาเรย์ในแกนแรก ถ้าต้องการกลับลำดับในแกนถัดมาก็ ar[:,::-1]
กรณีสองมิติ ถ้าต้องการกลับแนวตั้งเขียนเป็น [::-1] ถ้ากลับแนวนอนเขียนเป็น [:,::-1] ถ้ากลับทั้งสองแนวก็เป็น [::-1,::-1]
ตัวอย่าง
ผลลัพธ์
อ้างอิง
การขึ้นรูปใหม่
เราสามารถนำสมาชิกในอาเรย์มาจัดเรียงใหม่ได้ด้วยการใช้เมธอด reshape โดยกำหนดรูปร่างใหม่ของอาเรย์
reshape เป็นเมธอดที่จะทำการคืนอาเรย์ใหม่ที่มีขนาดมิติเท่ากับที่กำหนด
import numpy as np
arr = np.arange(8)
print(arr.reshape(2,4))
arr = np.arange(8)
print(arr.reshape(2,4))
ผลลัพธ์
[[0 1 2 3]
[4 5 6 7]]
[4 5 6 7]]
รูปร่างใหม่ของอาเรย์จำเป็นจะต้องรองรับสมาชิกเท่ากับจำนวนสมาชิกในอาเรย์เดิม ไม่เช่นนั้นจะเกิดข้อผิดพลาด
arr = np.arange(10)
print(arr.reshape(3,3)) # ได้ ValueError: total size of new array must be unchanged
print(arr.reshape(3,3)) # ได้ ValueError: total size of new array must be unchanged
มีเมธอดอีกตัวที่คล้ายๆกันคือ resize ซึ่งมีหน้าที่เปลี่ยนแปลงโครงสร้างของอาเรย์ที่นำมากระทำให้เป็นไปตามที่กำหนด
resize จะไม่คืนค่าอะไรกลับมา แต่จะเป็นการเปลี่ยนรูปของอาเรย์นั้นไปเลย ต่างจาก reshape ซึ่งแค่ไว้คืนค่ากลับมาโดยไม่ได้เปลี่ยนตัวอาเรย์นั้นเอง
arr.resize(n,m) เทียบเท่ากับ arr = arr.reshape(n,m)
ตัวอย่าง
arr = np.arange(8)
arr.resize(2,4)
print(arr)
arr.resize(2,4)
print(arr)
ผลลัพธ์
[[0 1 2 3]
[4 5 6 7]]
[4 5 6 7]]
การยุบให้เหลือมิติเดียว
บางครั้งเราอาจมีอาเรย์สองมิติขึ้นไปอยู่แต่ต้องการยุบให้เหลือมิติเดียวเพื่อความสะดวกในการใช้งานบางอย่าง
กรณีแบบนี้จะใช้คำสั่ง reshape แล้วใส่ค่าเป็นจำนวนสมาชิกของอาเรย์ก็ได้ แต่ว่ามีคำสั่งสำหรับการนี้โดยเฉพาะซึ่งใช้งานได้ง่ายกว่านั้น นั่นคือ flatten กับ ravel
ตัวอย่างการใช้ flatten
ioooioooi = np.eye(3,3)
print(ioooioooi)
ioooioooi = ioooioooi.flatten()
print(ioooioooi)
print(ioooioooi)
ioooioooi = ioooioooi.flatten()
print(ioooioooi)
ผลลัพธ์
[[ 1. 0. 0.]
[ 0. 1. 0.]
[ 0. 0. 1.]]
[ 1. 0. 0. 0. 1. 0. 0. 0. 1.]
[ 0. 1. 0.]
[ 0. 0. 1.]]
[ 1. 0. 0. 0. 1. 0. 0. 0. 1.]
ตัวอย่างนี้จะใช้ ravel ก็ได้ผลแบบเดียวกัน
ข้อแตกต่างของ ravel กับ flatten ก็คือ flatten จะทำการคัดลอกสมาชิกในอาเรย์มา ในขณะที่ ravel จะแค่คืนค่ามุมมองที่อ้างอิงถึง
ลองยกตัวอย่างให้เห็นความแตกต่าง
x = np.array(((1,2,3),(4,5,6),(7,8,9)))
xfla = x.flatten()
xfla[0] = 100
print(xfla)
print(x)
xfla = x.flatten()
xfla[0] = 100
print(xfla)
print(x)
ผลลัพธ์
[100 2 3 4 5 6 7 8 9]
[[1 2 3]
[4 5 6]
[7 8 9]]
[[1 2 3]
[4 5 6]
[7 8 9]]
xra = x.ravel()
xra[0] = 0
print(xra)
print(x)
xra[0] = 0
print(xra)
print(x)
ผลลัพธ์
[0 2 3 4 5 6 7 8 9]
[[0 2 3]
[4 5 6]
[7 8 9]]
[[0 2 3]
[4 5 6]
[7 8 9]]
จะเห็นว่า xfla ใช้ flatten ซึ่งเป็นการคัดลอกค่าแล้วสร้างข้อมูลขึ้นใหม่ ดังนั้นพอมีการแก้ไขค่าใน xfla ก็ไม่ได้กระทบอะไรกับ x
แต่ว่า xra นั้นใช้ ravel เป็นแค่การดึงมุมมองมาใช้ไม่ได้สร้างข้อมูลใหม่ ยังใช้หน่วยความจำเดียวกันกับ x อยู่ ดังนั้นพอมีการแก้ไขค่าใน xra แล้ว ค่าใน x ก็จะเปลี่ยนตาม
ravel จะเขียนในรูปฟังก์ชันหรือเมธอดก็ได้ เช่น np.ravel(x) มีค่าเท่ากับ x.ravel() แต่ไม่สามารถเขียน np.flatten(x) ได้ ต้องเขียน x.flatten() เท่านั้น
การสลับแกนของอาเรย์
สำหรับอาเรย์สองมิติสามารถสลับแกนได้ด้วยคำสั่ง transpose จะเขียนในรูปเมธอดหรือฟังก์ชันก็ได้
x = np.array(((1,2,3),(4,5,6)))
print(x)
print(np.transpose(x))
print(x.transpose())
print(x)
print(np.transpose(x))
print(x.transpose())
ผลลัพธ์
[[1 2 3]
[4 5 6]]
[[1 4]
[2 5]
[3 6]]
[[1 4]
[2 5]
[3 6]]
[4 5 6]]
[[1 4]
[2 5]
[3 6]]
[[1 4]
[2 5]
[3 6]]
นอกจาก นี้ยังอาจหาค่าทรานสโพสได้อย่างง่ายๆโดยเขียนต่อท้ายอาเรย์ด้วย .T ก็ได้ ข้อแตกต่างคือ .T ไม่ใช่เมธอด ไม่ต้องมีวงเล็บ () ต่อท้าย
print(np.array([[1],[2],[3]]).T) ได้ # [[1 2 3]]
สำหรับมิติที่สูงขึ้นไปใช้เมธอด swapaxes โดยใส่เลขของมิติ (แกน) ทั้งสองที่ต้องการสลับลงไป โดยมิติแรกนับเป็น 0
ถ้าใช้กับสองมิติ ใส่เป็น (0,1) จะได้ผลเหมือนกับ transpose
x = np.array([[1,2],[3,4],[5,6]])
print(x)
print(x.swapaxes(0,1))
print(x)
print(x.swapaxes(0,1))
ผลลัพธ์
[[1 2]
[3 4]
[5 6]]
[[1 3 5]
[2 4 6]]
[3 4]
[5 6]]
[[1 3 5]
[2 4 6]]
swapaxes จะเขียนในรูปฟังก์ชันก็ได้เช่นกัน คือ np.swapaxes(x,0,1)
การเพิ่มมิติขึ้นมา
ปกติแล้วคำสั่ง transpose หรือ T จะใช้กับที่เป็นสองอาเรย์สองมิติ หากใช้กับอาเรย์ที่เป็นหนึ่งมิติจะไม่มีการเปลี่ยนแปลง
print(np.arange(4).T) # ได้ [0 1 2 3]
หากต้องการจะนำอาเรย์หนึ่งมิติมาสลับเปลี่ยนการจับวางสลับแถวในสองมิติเราจะ เป็นต้องทำการเพิ่มมิตินั้นสามารถทำได้ด้วยวิธีการที่อาจจะดูแปลกสักหน่อย นั่นคือเติม [None] ไว้ข้างท้ายอาเรย์ มิติก็จะเพิ่มขึ้นมาทันที
เช่น
print(np.arange(4)[None]) # ได้ [[0 1 2 3]]
แบบนี้ก็จะได้อาเรย์สองมิติ แม้ว่าแกนตั้งจะมีแค่แถวเดียวก็ตาม
เท่านี้ก็สามารถนำมาทรานสโพสได้
print(np.arange(4)[None].T)
# ได้
# [[0]
# [1]
# [2]
# [3]]
# ได้
# [[0]
# [1]
# [2]
# [3]]
นอกจากนี้เราอาจสลับแกนได้ทันทีด้วยการเติม :, ไว้ด้านหน้า None
print(np.arange(4)[:,None]) # ผลได้เหมือนตัวอย่างที่แล้ว
หากใช้กับอาเรย์สองมิติก็จะกลายเป็นอาเรย์สามมิติได้
นั่นหมายความว่าจากอาเรย์หนึ่งมิติหากใส่ [None] ๒ ครั้งก็จะกลายเป็นสามมิติได้
print(np.arange(4)[None][None]) # ได้ [[[0 1 2 3]]]
print(np.arange(4)[None,None]) # แบบนี้ก็ได้เหมือนกัน
print(np.arange(4)[None,None]) # แบบนี้ก็ได้เหมือนกัน
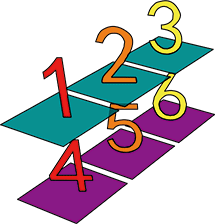
เราสามารถใช้วิธีนี้เพื่อสลับแกนของอาเรย์สองมิติไปอยู่ในมิติที่สามได้
a = np.array([[1,2,3],[4,5,6]])
print(a)
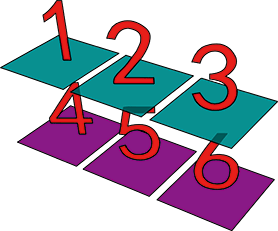
#***ภาพเหล่านี้สร้างด้วยมายาไพธอน
print(a[:,None])
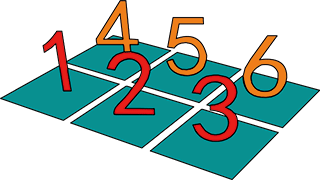
print(a[:,:,None])
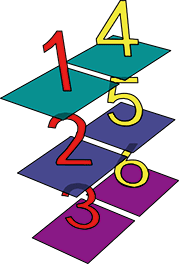
print(a.T[:,None])
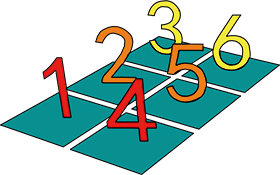
print(a.T[:,:,None])
print(a)

#***ภาพเหล่านี้สร้างด้วยมายาไพธอน
print(a[:,None])

print(a[:,:,None])

print(a.T[:,None])

print(a.T[:,:,None])

นอกจากนี้แล้วยังมีวิธีการอีกอย่างที่ให้ผลเหมือนกัน คือใช้ฟังก์ชัน np.expand_dims
| np.expand_dims(a,axis=0) | เท่ากับ a[None] |
| np.expand_dims(a,axis=1) | เท่ากับ a[:,None] |
| np.expand_dims(a,axis=2) | เท่ากับ a[:,:,None] |
แต่เนื่องจากเขียนยาวกว่าจึงดูเหมือนจะไม่เป็นที่นิยมนัก ใช้ [None] ง่ายกว่า แม้จะดูแล้วอาจเข้าใจยากสักหน่อยก็ตาม
เพื่อให้เข้าใจการทำงานของ None มากขึ้นอาจลองดูตัวอย่างนี้
d = np.array([[3,2,1],[4,6,7]])
print(d.shape) # ได้ (2, 3)
print(d[None].shape) # ได้ (1, 2, 3)
print(d[None,:,:].shape) # ได้ (1, 2, 3)
print(d[:,None].shape) # ได้ (2, 1, 3)
print(d[:,None,:].shape) # ได้ (2, 1, 3)
print(d[:,:,None].shape) # ได้ (2, 3, 1)
print(d.shape) # ได้ (2, 3)
print(d[None].shape) # ได้ (1, 2, 3)
print(d[None,:,:].shape) # ได้ (1, 2, 3)
print(d[:,None].shape) # ได้ (2, 1, 3)
print(d[:,None,:].shape) # ได้ (2, 1, 3)
print(d[:,:,None].shape) # ได้ (2, 3, 1)
จะเห็นว่า None เข้าไปแทนตำแหน่งแกนไหนตรงนั้นจะมีขนาดเป็น 1 ส่วนแกนที่เหลือก็จะได้มิติตามอาเรย์เดิม
ที่จริงแล้ว None ซึ่งถูกใช้ในกรณีนี้มักถูกใช้เป็น np.newaxis มากกว่า เพราะดูแล้วเหมือนเข้าใจได้ง่าย แต่ np.newaxis ก็เป็นเหมือนตัวแปรตัวแทนของ None
print(np.newaxis) # ได้ None
ดังนั้นจึงไม่มีความจำเป็นต้องใช้ np.newaxis จริงๆ แต่อย่างไรก็ตามก็แล้วแต่คน หากเห็นว่า None มันดูไม่สวย ดูแล้วไม่สื่อความหมาย ก็อาจใช้ np.newaxis ก็ได้
การนำอาเรย์มาต่อเข้าด้วยกัน
numpy มีคำสั่งที่สะดวกที่ใช้ในการเอาอาเรย์มาต่อกัน ได้แก่
| np.concatenate( (a, b),axis=i) | นำอาเรย์มารวมกันตามแกนที่ i เมื่อรวมกันแล้วจะได้มิติเท่าเดิม |
| np.stack( (a, b),axis=i) | นำอาเรย์มารวมกันให้ได้มิติเพิ่มขึ้นหนึ่งมิติ |
| np.hstack( (a, b) ) | นำอาเรย์มารวมกันตามมิติที่หนึ่ง |
| np.vstack( (a, b) ) | นำอาเรย์มารวมกันตามมิติที่สอง |
| np.column_stack( (a, b) ) | นำอาเรย์หนึ่งมิติมารวมกันในอีกมิติแล้วทรานสโพส ผลเหมือน np.vstack( (a, b) ).T |
การต่อกันของอาเรย์นั้นในบางกรณีจะทำให้มิติเพิ่มขึ้นมาอีกหนึ่งได้ แต่บางทีก็อาจไม่เพิ่ม แล้วแต่กรณีและฟังก์ชันที่ใช้
ที่จริงแล้วมีอีกฟังก์ชันหนึ่งซึ่งใช้รวมอาเรย์ให้เป็นสามมิติ นั่นคือ np.dstack แต่สำหรับกรณีที่ได้สามมิตินั้นจะค่อนข้างซับซ้อน จะยังขอไม่พูดถึงตอนนี้มากแต่ยกไปเน้นในบทที่ ๒๓
ถ้าใช้กับอาเรย์หนึ่งมิติ
- hstack จะเป็นการเอาอาเรย์มาต่อกัน เท่ากับ np.concatenate( (a, b),axis=0)
- vstack จะเป็นการรวมกันให้เป็นหลายแถว เท่ากับ np.stack( (a,b),axis=0)
ตัวอย่าง
a = [1,1,1]
b = [2,2,2]
print(np.hstack((a,b))) # ได้ [1 1 1 2 2 2]
print(np.vstack((a,b))) # หรือ np.stack((a,b),axis=0)
# ได้
# [[1 1 1]
# [2 2 2]]
print(np.stack((a,b),axis=1)) # หรือ print(np.column_stack((a,b)))
# ได้
# [[1 2]
# [1 2]
# [1 2]]
print(np.concatenate((a,b),axis=0)) # ได้ [1 1 1 2 2 2]
b = [2,2,2]
print(np.hstack((a,b))) # ได้ [1 1 1 2 2 2]
print(np.vstack((a,b))) # หรือ np.stack((a,b),axis=0)
# ได้
# [[1 1 1]
# [2 2 2]]
print(np.stack((a,b),axis=1)) # หรือ print(np.column_stack((a,b)))
# ได้
# [[1 2]
# [1 2]
# [1 2]]
print(np.concatenate((a,b),axis=0)) # ได้ [1 1 1 2 2 2]
ถ้าใช้กับอาเรย์สองมิติ
- hstack จะเป็นการรวมกันตามแนวนอน เท่ากับ np.concatenate( (a, b),axis=1)
- vstack จะเป็นการรวมกันตามแนวตั้ง เท่ากับ np.concatenate( (a, b),axis=0)
- stack จะเป็นการรวมกันในแนวมิติที่สาม
ตัวอย่าง
a = [[1,1,1],[2,2,2]]
b = [[3,3,3],[4,4,4]]
print(np.hstack((a,b))) # หรือ print(np.concatenate((a,b),axis=1))
# ได้
# [[1 1 1 3 3 3]
# [2 2 2 4 4 4]]
print(np.vstack((a,b))) # หรือ print(np.concatenate((a,b),axis=0))
# ได้
# [[1 1 1]
# [2 2 2]
# [3 3 3]
# [4 4 4]]
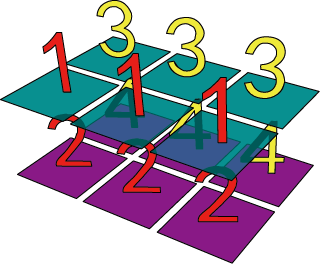
print(np.stack((a,b)))
# ได้อาเรย์สามมิติดังภาพ
b = [[3,3,3],[4,4,4]]
print(np.hstack((a,b))) # หรือ print(np.concatenate((a,b),axis=1))
# ได้
# [[1 1 1 3 3 3]
# [2 2 2 4 4 4]]
print(np.vstack((a,b))) # หรือ print(np.concatenate((a,b),axis=0))
# ได้
# [[1 1 1]
# [2 2 2]
# [3 3 3]
# [4 4 4]]
print(np.stack((a,b)))
# ได้อาเรย์สามมิติดังภาพ

การแยกอาเรย์
หากต้องการแยกอาเรย์ออกเป็นส่วนๆไว้ในลิสต์ มีฟังก์ชันกลุ่มหนึ่งที่สามารถใช้ได้
| split( (a, n),axis=i) | แยกอาเรย์ตามแกนที่ i ออกเป็น n ส่วน |
| hsplit( (a, n),axis=i) | แยกอาเรย์ตามมิติที่หนึ่ง ออกเป็น n ส่วน |
| vsplit( (a, n),axis=i) | แยกอาเรย์ตามมิติที่สอง ออกเป็น n ส่วน |
นอกจากนี้ก็มี dsplit ซึ่งเอาไว้แยกตามมิติที่สาม
ตัวอย่าง
a = np.arange(1,7).reshape(2,3)
print(np.hsplit(a,3)) # หรือ print(np.split(a,3,axis=1))
# ได้
# [array([[1],
# [4]]), array([[2],
# [5]]), array([[3],
# [6]])]
print(np.vsplit(a,2)) # ได้ [array([[1, 2, 3]]), array([[4, 5, 6]])]
print(np.split(a,2)) # ได้ [array([[1, 2, 3]]), array([[4, 5, 6]])]
print(np.hsplit(a,3)) # หรือ print(np.split(a,3,axis=1))
# ได้
# [array([[1],
# [4]]), array([[2],
# [5]]), array([[3],
# [6]])]
print(np.vsplit(a,2)) # ได้ [array([[1, 2, 3]]), array([[4, 5, 6]])]
print(np.split(a,2)) # ได้ [array([[1, 2, 3]]), array([[4, 5, 6]])]
การจะใช้ฟังก์ชันแยกอาเรย์ได้นั้นจำนวนส่วนที่แบ่งจะต้องหารลงตัวกับจำนวนแถวหรือหลัก
การซ้ำอาเรย์
หากต้องการนำอาเรย์ตัวเดิมมาต่อกันหลายๆครั้งสามารถใช้ฟังก์ชัน np.tile
การใช้คือ np.tile(อาเรย์, จำนวนที่ซ้ำ)
ตัวอย่าง
a = np.arange(1,7).reshape(2,3)
print(a)
# ได้
# [[1 2 3]
# [4 5 6]]
print(np.tile(a,3))
# ได้
# [[1 2 3 1 2 3 1 2 3]
# [4 5 6 4 5 6 4 5 6]]
print(a)
# ได้
# [[1 2 3]
# [4 5 6]]
print(np.tile(a,3))
# ได้
# [[1 2 3 1 2 3 1 2 3]
# [4 5 6 4 5 6 4 5 6]]
การใส่อาร์กิวเมนต์ตัวหลังเป็นแค่ตัวเลขเดี่ยวจะเป็นการซ้ำในแนวแกนสุดท้าย แต่ถ้าต้องการให้ซ้ำในแนวอื่นต้องเปลี่ยนเป็นใส่ทูเพิล
print(np.tile(a,(2,1)))
ได้
[[1 2 3]
[4 5 6]
[1 2 3]
[4 5 6]]
[4 5 6]
[1 2 3]
[4 5 6]]
print(np.tile(a,(2,3)))
ได้
[[1 2 3 1 2 3 1 2 3]
[4 5 6 4 5 6 4 5 6]
[1 2 3 1 2 3 1 2 3]
[4 5 6 4 5 6 4 5 6]]
[4 5 6 4 5 6 4 5 6]
[1 2 3 1 2 3 1 2 3]
[4 5 6 4 5 6 4 5 6]]
อีกตัวหนึ่งที่มีไว้สำหรับซ้ำอาเรย์เหมือนกันคือ np.repeat แต่จะต่างกันเล็กน้อยคือ repeat จะนำเอาอาเรย์มายุบเหลือมิติเดียว จากนั้นทำซ้ำโดยเอาตัวเดิมอยู่ติดกัน
ตัวอย่าง
a = np.arange(1,7).reshape(2,3)
print(a)
print(np.repeat(a,3))
print(a)
print(np.repeat(a,3))
ได้
[[1 2 3]
[4 5 6]]
[1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6]
[4 5 6]]
[1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6]
จะเห็นว่าแม้จะใช้อาเรย์สองมิติ แต่ก็ถูกยุบรวมเหลือมิติเดียว
หากต้องการให้คิดมิติด้วยก็เพิ่มคีย์เวิร์ด axis ลงไป
print(np.repeat(a,3,axis=0)) # ซ้ำตามแนวตั้ง
print(np.repeat(a,3,axis=1)) # ซ้ำตามแนวนอน
print(np.repeat(a,3,axis=1)) # ซ้ำตามแนวนอน
ได้
[[1 2 3]
[1 2 3]
[1 2 3]
[4 5 6]
[4 5 6]
[4 5 6]]
[[1 1 1 2 2 2 3 3 3]
[4 4 4 5 5 5 6 6 6]]
[1 2 3]
[1 2 3]
[4 5 6]
[4 5 6]
[4 5 6]]
[[1 1 1 2 2 2 3 3 3]
[4 4 4 5 5 5 6 6 6]]
การกลับลำดับอาเรย์
numpy ไม่มีฟังก์ชันสำหรับกลับลำดับของอาเรย์โดยเฉพาะ แต่สามารถกลับลำดับของอาเรย์ได้โดยการเขียนแบบนี้ ar[::-1] แบบนี้จะเป็นการกลับลำดับของอาเรย์ในแกนแรก ถ้าต้องการกลับลำดับในแกนถัดมาก็ ar[:,::-1]
กรณีสองมิติ ถ้าต้องการกลับแนวตั้งเขียนเป็น [::-1] ถ้ากลับแนวนอนเขียนเป็น [:,::-1] ถ้ากลับทั้งสองแนวก็เป็น [::-1,::-1]
ตัวอย่าง
arii = np.arange(1,10).reshape(3,3)
print(arii)
print(arii[::-1])
print(arii[:,::-1])
print(arii[::-1,::-1])
print(arii)
print(arii[::-1])
print(arii[:,::-1])
print(arii[::-1,::-1])
ผลลัพธ์
[[1 2 3]
[4 5 6]
[7 8 9]]
[[7 8 9]
[4 5 6]
[1 2 3]]
[[3 2 1]
[6 5 4]
[9 8 7]]
[[9 8 7]
[6 5 4]
[3 2 1]]
[4 5 6]
[7 8 9]]
[[7 8 9]
[4 5 6]
[1 2 3]]
[[3 2 1]
[6 5 4]
[9 8 7]]
[[9 8 7]
[6 5 4]
[3 2 1]]
อ้างอิง
http://www.turbare.net/transl/scipy-lecture-notes/intro/numpy/array_object.html
http://rest-term.com/archives/2999
http://seesaawiki.jp/met-python/d/array
http://www.kamishima.net/mlmpyja/nbayes2/shape.html
http://nkmk.github.io/blog/python-numpy-join-split
http://rest-term.com/archives/2999
http://seesaawiki.jp/met-python/d/array
http://www.kamishima.net/mlmpyja/nbayes2/shape.html
http://nkmk.github.io/blog/python-numpy-join-split