[python] จากการวิเคราะห์การถดถอยเชิงเส้นสู่ปัญหาการจำแนกประเภท
เขียนเมื่อ 2016/12/24 00:46
แก้ไขล่าสุด 2022/07/21 15:30
บทความนี้เขียนต่อยอดจากเรื่องการวิเคราะห์การถดถอยเชิงเส้นที่เขียนไปใน https://phyblas.hinaboshi.com/20161210
และ https://phyblas.hinaboshi.com/20161212
เพื่อเป็นพื้นฐานที่เชื่อมไปสู่เนื้อหาเรื่องปัญหาการจำแนกประเภทด้วยการวิเคราะห์การถดถอยโลจิสติก
การวิเคราะห์การถดถอยเชิงเส้นเป็นการหาความสัมพันธ์ระหว่างตัวแปรต้นกับผลลัพธ์ โดยผลลัพธ์ที่ได้นั้นจะเป็นตัวเลข ซึ่งอาจจะมีค่าเป็นตัวเลขเท่าไหร่ก็ได้
อย่างไรก็ตาม มีปัญหาอีกประเภทหนึ่ง ซึ่งผลลัพธ์ที่สนใจนั้นไม่ใช่ค่าตัวเลขเท่าไหร่ก็ได้ แต่เป็นแค่บอกว่าผลลัพธ์นั้นถูกจัดอยู่ในกลุ่มประเภทไหน แบบนี้เรียกว่าปัญหาการจำแนกประเภทข้อมูล
ปัญหาการจำแนกประเภทที่เรียบง่ายที่สุดคือการจำแนกเป็นสองกลุ่ม ซึ่งต่อยอดมาจากแนวคิดของการวิเคราะห์การถดถอยเชิงเส้นได้โดยตรง
เพื่อให้เข้าใจง่ายก็ขอเริ่มอธิบายจากการยกตัวอย่างก่อน
สมมุติว่าปัญหาที่เราต้องการหาคือหาความสูงจากระดับน้ำทะเลของพื้นที่บริเวณหนึ่งซึ่งเขียนในรูปเชิงเส้นดังนี้
โดย f(x,y) คือความสูงของพื้น x คือพิกัดในแนวตะวันตกออก y คือพิกัดในแนวใต้เหนือ wx และ wy คือค่าน้ำหนักของ x และ y ส่วน b คือไบแอส
สมมุติว่าผลเฉลยที่เราได้มานั้นมีค่า wx=2, wy=3 และ b=-25 ซึ่งอาจเขียนเป็นฟังก์ชันได้ดังนี้
ลองวาดแผนภาพไล่สีแสดงความสูงต่ำของพื้นจะได้แบบนี้
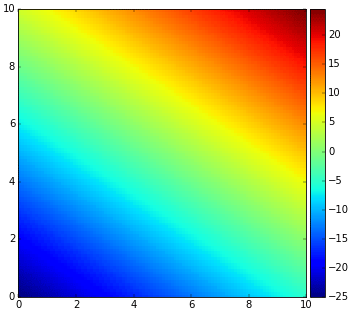
หรืออาจลองวาดเป็นสามมิติเพื่อแสดงความต่างระดับของพื้นได้แบบนี้
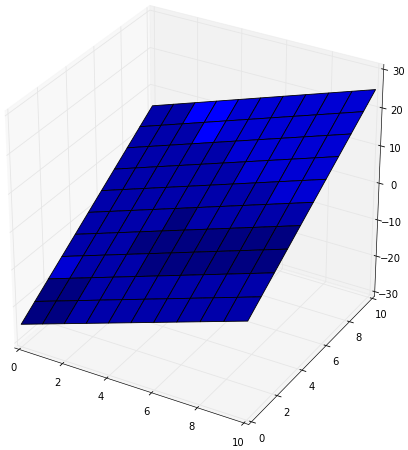
จะเห็นว่าฟังก์ชันแสดงความสูงของพื้นเป็นฟังก์ชันเชิงเส้นที่มีความต่อเนื่อง ค่าที่ได้จะเป็นเท่าไหร่ก็ได้ตั้งแต่ลบอนันต์ถึงอนันต์
แต่หากเปลี่ยนปัญหามาเป็นปัญหาการจำแนกประเภท นั่นคือเราจะแบ่งคำตอบที่ได้นี้ออกเป็นสองส่วน คือส่วนที่สูงกว่า 0 และที่ต่ำกว่า 0
สิ่งที่เรารู้ได้อีกอย่างจากค่าความสูงที่ได้นี้ก็คือว่าตำแหน่งตรงนั้นอยู่เหนือระดับน้ำทะเลหรือไม่ โดยดูว่าค่าสูงหรือต่ำกว่า 0 ในบางกรณีนี่อาจเป็นคำถามที่สำคัญมากกว่าที่จะบอกว่าสูงเท่าไหร่ เพราะเหนือน้ำไม่ว่าเหนือแค่ไหนก็จะเป็นแผ่นดิน ใต้น้ำไม่ว่าจะลึกแค่ไหนก็คือทะเล
พอลองเปลี่ยนโจทย์ใหม่เป็นพิจารณาว่าพื้นที่นั้นอยู่เหนือระดับน้ำทะเลหรือไม่ คำตอบจากที่เดิมทีเป็นเท่าไหร่ก็ได้นั้นจะเหลือเพียงแค่สองคำตอบ คือจริงกับเท็จเท่านั้น
ซึ่งโดยทั่วไปแล้วมักจะแทนค่าที่เป็นจริงเป็น 1 และค่าเท็จแทนด้วย 0
ปกติในไพธอนเวลาเอาค่าตัวเลขอะไรมาเข้านิพจน์ที่ใส่ >, <, <=, >=, == แบบนี้จะได้ผลเป็นค่า True และ False ซึ่งเทียบเท่ากับค่า 1 และ 0 อยู่แล้ว สามารถเอาค่าที่ได้จากสมการหรืออสมการแบบนี้มาใส่เป็นผลลัพธ์ได้เลย จะได้ผลที่มีแต่ค่า 0 กับ 1 ทันที
หากลองเขียนแผนภาพไล่สีดูจะได้ในลักษณะแบบนี้
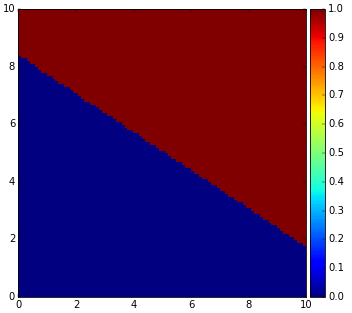
ค่าที่ได้มีเพียงสองค่าเท่านั้นคือ 0 และ 1 โดยจุดตัดเปลี่ยนคือบริเวณที่ผลจากฟังก์ชันเดิมเป็น 0 จากภาพนี้ส่วนสีน้ำเงินคือทะเล ส่วนสีแดงคือแผ่นดิน
ปกติแล้วจะใช้ค่าที่ใช้แบ่งจะเป็นจุดที่ฟังก์ชันเดิมได้ค่าเป็น 0 เสมอ ถ้าต้องการเปลี่ยนแปลงก็จะไปปรับที่ไบแอสของฟังก์ชันแทน
เช่น ถ้าแก้ใหม่เป็นว่าถ้าระดับน้ำสูงขึ้นอีก 5 เมตรส่วนไหนจะเป็นแผ่นดินหรือทะเล อสมการก็จะแก้เป็น 2*x+3*3-20 > 0 แทนที่จะเป็น 2*x+3*3-25 > 5
ในปัญหาการถดถอยเชิงเส้นอาจเป็นในลักษณะที่ว่า เรารู้ค่าความสูงในบางจุดแล้วต้องการหาว่าความสูงในจุดใดๆนั้นมีค่าเป็นเท่าไหร่ โดยทำนายจากจุดที่รู้
เช่นสมมุติว่าสุ่มสำรวจความสูงของพื้นในแต่ละจุดแล้วได้ผลออกมาดังรูปนี้
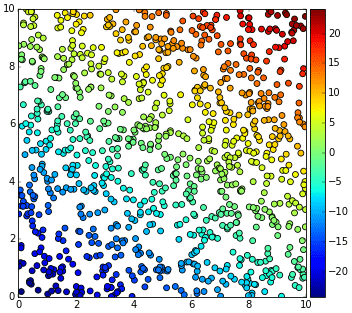
แต่ในปัญหาการจำแนกประเภทอาจเปลี่ยนคำถามเป็นว่าเรารู้ว่าตรงนั้นตรงนี้สูงกว่าระดับน้ำ (เป็นแผ่นดิน) หรือต่ำกว่าระดับน้ำ (เป็นทะเล) แล้วต้องการทำนายว่าบริเวณอื่นที่ไม่มีข้อมูลนั้นสูงหรือต่ำกว่า
หากวาดภาพดูก็จะเป็นในลักษณะแบบนี้
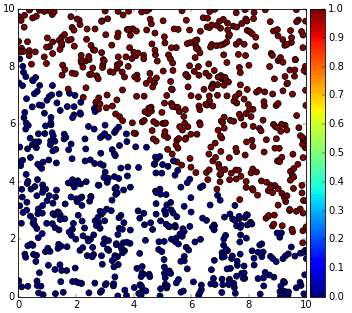
ในปัญหาการถดถอยเชิงเส้นเราจะสมมุติสมการเชิงเส้นขึ้นมาแล้วปรับค่าน้ำหนักและไบแอสไปเรื่อยๆเพื่อให้ค่าความคลาดเคลื่อนน้อยที่สุด ดังที่ได้เขียนถึงไปแล้ว
ส่วนหลักการแก้ปัญหาการจำแนกประเภทนั้นก็สามารถใช้แนวทางเดียวกัน เพียงแต่ว่าหลักการคิดค่าความคลาดเคลื่อนจะต้องมาพิจารณาใหม่เพื่อหาวิธีที่เหมาะสม
แนวคิดในเรื่องนี้มีอยู่หลากหลายด้วยกัน โดยวิธีที่ดูจะเรียบง่ายเป็นพื้นฐานที่สุดก็คือเทคนิคที่เรียกว่าเพอร์เซ็ปตรอน (感知器, perceptron)
หลักการของเพอร์เซ็ปตรอนก็คือจะคิดค่าความคลาดเคลื่อนโดยนับจำนวนของคำตอบที่ทายผิด แล้วนำค่านั้นมาใช้ปรับปรุงค่าน้ำหนักและไบแอส
แนวคิดของเพอร์เซ็ปตรอนนั้นดูจะเรียบง่าย แต่ก็มีข้อด้อยทำให้ไม่ดีพอที่จะใช้งานจริงนัก เพราะการตัดสินความคลาดเคลื่อนแค่การดูว่าผิดหรือถูกเป็นการคิดที่หยาบเกินไป
วิธีที่ซับซ้อนขึ้นมาหน่อยแต่ได้ผลกว่าและนิยมนำมาใช้งานจริงก็คือ การถดถอยโลจิสติก (逻辑回归, logistic regression) ซึ่งใช้ฟังก์ชันซิกมอยด์ (sigmoid) ในการคำนวณคำตอบในรูปของความน่าจะเป็น แทนที่จะแบ่งคำตอบเป็น 0 หรือ 1 ทันที
เรื่องของการวิเคราะห์การถดถอยโลจิสติกอ่านได้ใน https://phyblas.hinaboshi.com/20161103
อ้างอิง
และ https://phyblas.hinaboshi.com/20161212
เพื่อเป็นพื้นฐานที่เชื่อมไปสู่เนื้อหาเรื่องปัญหาการจำแนกประเภทด้วยการวิเคราะห์การถดถอยโลจิสติก
การวิเคราะห์การถดถอยเชิงเส้นเป็นการหาความสัมพันธ์ระหว่างตัวแปรต้นกับผลลัพธ์ โดยผลลัพธ์ที่ได้นั้นจะเป็นตัวเลข ซึ่งอาจจะมีค่าเป็นตัวเลขเท่าไหร่ก็ได้
อย่างไรก็ตาม มีปัญหาอีกประเภทหนึ่ง ซึ่งผลลัพธ์ที่สนใจนั้นไม่ใช่ค่าตัวเลขเท่าไหร่ก็ได้ แต่เป็นแค่บอกว่าผลลัพธ์นั้นถูกจัดอยู่ในกลุ่มประเภทไหน แบบนี้เรียกว่าปัญหาการจำแนกประเภทข้อมูล
ปัญหาการจำแนกประเภทที่เรียบง่ายที่สุดคือการจำแนกเป็นสองกลุ่ม ซึ่งต่อยอดมาจากแนวคิดของการวิเคราะห์การถดถอยเชิงเส้นได้โดยตรง
เพื่อให้เข้าใจง่ายก็ขอเริ่มอธิบายจากการยกตัวอย่างก่อน
สมมุติว่าปัญหาที่เราต้องการหาคือหาความสูงจากระดับน้ำทะเลของพื้นที่บริเวณหนึ่งซึ่งเขียนในรูปเชิงเส้นดังนี้
f(x,y) = wx*x + wy*y + b
โดย f(x,y) คือความสูงของพื้น x คือพิกัดในแนวตะวันตกออก y คือพิกัดในแนวใต้เหนือ wx และ wy คือค่าน้ำหนักของ x และ y ส่วน b คือไบแอส
สมมุติว่าผลเฉลยที่เราได้มานั้นมีค่า wx=2, wy=3 และ b=-25 ซึ่งอาจเขียนเป็นฟังก์ชันได้ดังนี้
def f(x,y):
return 2*x+3*y-25
return 2*x+3*y-25
ลองวาดแผนภาพไล่สีแสดงความสูงต่ำของพื้นจะได้แบบนี้
import numpy as np
import matplotlib.pyplot as plt
x,y = np.meshgrid(np.linspace(0,10,101),np.linspace(0,10,101))
z = f(x,y)
plt.axes(aspect=1)
plt.pcolormesh(x,y,z,cmap='jet')
plt.colorbar(pad=0.01)
plt.show()
import matplotlib.pyplot as plt
x,y = np.meshgrid(np.linspace(0,10,101),np.linspace(0,10,101))
z = f(x,y)
plt.axes(aspect=1)
plt.pcolormesh(x,y,z,cmap='jet')
plt.colorbar(pad=0.01)
plt.show()

หรืออาจลองวาดเป็นสามมิติเพื่อแสดงความต่างระดับของพื้นได้แบบนี้
from mpl_toolkits import mplot3d
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.plot_surface(x,y,z,rstride=10,cstride=10)
plt.show()
plt.figure(figsize=[8,8])
ax = plt.axes([0,0,1,1],projection='3d')
ax.plot_surface(x,y,z,rstride=10,cstride=10)
plt.show()

จะเห็นว่าฟังก์ชันแสดงความสูงของพื้นเป็นฟังก์ชันเชิงเส้นที่มีความต่อเนื่อง ค่าที่ได้จะเป็นเท่าไหร่ก็ได้ตั้งแต่ลบอนันต์ถึงอนันต์
แต่หากเปลี่ยนปัญหามาเป็นปัญหาการจำแนกประเภท นั่นคือเราจะแบ่งคำตอบที่ได้นี้ออกเป็นสองส่วน คือส่วนที่สูงกว่า 0 และที่ต่ำกว่า 0
สิ่งที่เรารู้ได้อีกอย่างจากค่าความสูงที่ได้นี้ก็คือว่าตำแหน่งตรงนั้นอยู่เหนือระดับน้ำทะเลหรือไม่ โดยดูว่าค่าสูงหรือต่ำกว่า 0 ในบางกรณีนี่อาจเป็นคำถามที่สำคัญมากกว่าที่จะบอกว่าสูงเท่าไหร่ เพราะเหนือน้ำไม่ว่าเหนือแค่ไหนก็จะเป็นแผ่นดิน ใต้น้ำไม่ว่าจะลึกแค่ไหนก็คือทะเล
พอลองเปลี่ยนโจทย์ใหม่เป็นพิจารณาว่าพื้นที่นั้นอยู่เหนือระดับน้ำทะเลหรือไม่ คำตอบจากที่เดิมทีเป็นเท่าไหร่ก็ได้นั้นจะเหลือเพียงแค่สองคำตอบ คือจริงกับเท็จเท่านั้น
ซึ่งโดยทั่วไปแล้วมักจะแทนค่าที่เป็นจริงเป็น 1 และค่าเท็จแทนด้วย 0
ปกติในไพธอนเวลาเอาค่าตัวเลขอะไรมาเข้านิพจน์ที่ใส่ >, <, <=, >=, == แบบนี้จะได้ผลเป็นค่า True และ False ซึ่งเทียบเท่ากับค่า 1 และ 0 อยู่แล้ว สามารถเอาค่าที่ได้จากสมการหรืออสมการแบบนี้มาใส่เป็นผลลัพธ์ได้เลย จะได้ผลที่มีแต่ค่า 0 กับ 1 ทันที
หากลองเขียนแผนภาพไล่สีดูจะได้ในลักษณะแบบนี้
z = f(x,y)>0
plt.axes(aspect=1)
plt.pcolormesh(x,y,z,cmap='jet')
plt.colorbar(pad=0.01)
plt.show()
plt.axes(aspect=1)
plt.pcolormesh(x,y,z,cmap='jet')
plt.colorbar(pad=0.01)
plt.show()

ค่าที่ได้มีเพียงสองค่าเท่านั้นคือ 0 และ 1 โดยจุดตัดเปลี่ยนคือบริเวณที่ผลจากฟังก์ชันเดิมเป็น 0 จากภาพนี้ส่วนสีน้ำเงินคือทะเล ส่วนสีแดงคือแผ่นดิน
ปกติแล้วจะใช้ค่าที่ใช้แบ่งจะเป็นจุดที่ฟังก์ชันเดิมได้ค่าเป็น 0 เสมอ ถ้าต้องการเปลี่ยนแปลงก็จะไปปรับที่ไบแอสของฟังก์ชันแทน
เช่น ถ้าแก้ใหม่เป็นว่าถ้าระดับน้ำสูงขึ้นอีก 5 เมตรส่วนไหนจะเป็นแผ่นดินหรือทะเล อสมการก็จะแก้เป็น 2*x+3*3-20 > 0 แทนที่จะเป็น 2*x+3*3-25 > 5
ในปัญหาการถดถอยเชิงเส้นอาจเป็นในลักษณะที่ว่า เรารู้ค่าความสูงในบางจุดแล้วต้องการหาว่าความสูงในจุดใดๆนั้นมีค่าเป็นเท่าไหร่ โดยทำนายจากจุดที่รู้
เช่นสมมุติว่าสุ่มสำรวจความสูงของพื้นในแต่ละจุดแล้วได้ผลออกมาดังรูปนี้
x = np.random.uniform(0,10,1000)
y = np.random.uniform(0,10,1000)
z = f(x,y)
plt.axes(aspect=1,xlim=[0,10],ylim=[0,10])
plt.scatter(x,y,50,c=z,edgecolor='k',cmap='jet')
plt.colorbar(pad=0.01)
plt.show()
y = np.random.uniform(0,10,1000)
z = f(x,y)
plt.axes(aspect=1,xlim=[0,10],ylim=[0,10])
plt.scatter(x,y,50,c=z,edgecolor='k',cmap='jet')
plt.colorbar(pad=0.01)
plt.show()

แต่ในปัญหาการจำแนกประเภทอาจเปลี่ยนคำถามเป็นว่าเรารู้ว่าตรงนั้นตรงนี้สูงกว่าระดับน้ำ (เป็นแผ่นดิน) หรือต่ำกว่าระดับน้ำ (เป็นทะเล) แล้วต้องการทำนายว่าบริเวณอื่นที่ไม่มีข้อมูลนั้นสูงหรือต่ำกว่า
หากวาดภาพดูก็จะเป็นในลักษณะแบบนี้
z = f(x,y)>0
plt.axes(aspect=1,xlim=[0,10],ylim=[0,10])
plt.scatter(x,y,50,c=z,edgecolor='k',cmap='jet')
plt.colorbar(pad=0.01)
plt.show()
plt.axes(aspect=1,xlim=[0,10],ylim=[0,10])
plt.scatter(x,y,50,c=z,edgecolor='k',cmap='jet')
plt.colorbar(pad=0.01)
plt.show()

ในปัญหาการถดถอยเชิงเส้นเราจะสมมุติสมการเชิงเส้นขึ้นมาแล้วปรับค่าน้ำหนักและไบแอสไปเรื่อยๆเพื่อให้ค่าความคลาดเคลื่อนน้อยที่สุด ดังที่ได้เขียนถึงไปแล้ว
ส่วนหลักการแก้ปัญหาการจำแนกประเภทนั้นก็สามารถใช้แนวทางเดียวกัน เพียงแต่ว่าหลักการคิดค่าความคลาดเคลื่อนจะต้องมาพิจารณาใหม่เพื่อหาวิธีที่เหมาะสม
แนวคิดในเรื่องนี้มีอยู่หลากหลายด้วยกัน โดยวิธีที่ดูจะเรียบง่ายเป็นพื้นฐานที่สุดก็คือเทคนิคที่เรียกว่าเพอร์เซ็ปตรอน (感知器, perceptron)
หลักการของเพอร์เซ็ปตรอนก็คือจะคิดค่าความคลาดเคลื่อนโดยนับจำนวนของคำตอบที่ทายผิด แล้วนำค่านั้นมาใช้ปรับปรุงค่าน้ำหนักและไบแอส
แนวคิดของเพอร์เซ็ปตรอนนั้นดูจะเรียบง่าย แต่ก็มีข้อด้อยทำให้ไม่ดีพอที่จะใช้งานจริงนัก เพราะการตัดสินความคลาดเคลื่อนแค่การดูว่าผิดหรือถูกเป็นการคิดที่หยาบเกินไป
วิธีที่ซับซ้อนขึ้นมาหน่อยแต่ได้ผลกว่าและนิยมนำมาใช้งานจริงก็คือ การถดถอยโลจิสติก (逻辑回归, logistic regression) ซึ่งใช้ฟังก์ชันซิกมอยด์ (sigmoid) ในการคำนวณคำตอบในรูปของความน่าจะเป็น แทนที่จะแบ่งคำตอบเป็น 0 หรือ 1 ทันที
เรื่องของการวิเคราะห์การถดถอยโลจิสติกอ่านได้ใน https://phyblas.hinaboshi.com/20161103
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib