[python] แยกแยะภาพตัวเลขที่เขียนด้วยลายมือด้วยวิธีการ k เฉลี่ย
เขียนเมื่อ 2017/12/28 21:32
แก้ไขล่าสุด 2021/09/28 16:42
ก่อนหน้านี้ได้ลองเขียนถึงการแยกแยะภาพตัวเลขที่เขียนด้วยลายมือในชุดข้อมูล MNIST มาก่อนแล้ว https://phyblas.hinaboshi.com/20170920
ที่ผ่านมาที่ใช้เป็นเทคนิคการเรียนรู้แบบมีผู้สอน ซึ่งก็คือมีการป้อนข้อมูลภาพตัวเลขพร้อมบอกเฉลยว่าภาพนั้นคือตัวเลขอะไร แบบนี้โปรแกรมก็จะเรียนรู้จากคำตอบที่ให้ไปแล้วหาความแตกต่างในแต่กลุ่ม
แต่คราวนี้จะลองมาใช้เทคนิคการเรียนรู้แบบไม่มีผู้สอนบ้าง นั่นคือจะป้อนแต่ข้อมูลภาพไปโดยไม่บอกว่าภาพนี้เป็นตัวเลขอะไร แล้วให้ลองไปแยกแยะแบ่งภาพเป็นกลุ่มๆเอาเอง
การทำแบบนี้ย่อมยากกว่าแน่นอน เพราะหากให้โปรแกรมแบ่งภาพตัวเลขเอาเองตามธรรมชาติโดยไม่มีมนุษย์ไปกำกับบอกมันจะคิดเองได้หรือว่านี่เป็นเลข 0,1,2,3,... ตามที่เราเข้าใจ
แต่ก็มีค่าพอที่จะลอง น่าสนใจในแง่ที่ว่าธรรมชาติจะสามารถแบ่งแยกแยะตัวเลขที่มนุษย์ใช้ในชีวิตประจำวันจนชินนี้ได้เองหรือเปล่า
วิธีที่จะใช้ในครั้งนี้คือวิธีการ k เฉลี่ย ซึ่งได้อธิบายไปแล้วใน https://phyblas.hinaboshi.com/20171220
โดยจะใช้ sklearn เพื่อความสะดวกในการเขียน https://phyblas.hinaboshi.com/20171224
เราจะลองนำข้อมูลรูปภาพตัวเลขทั้ง 70000 ตัวมาป้อนให้โปรแกรมลองทำการแบ่งกลุ่มดู แล้วดูว่ามันจะแบ่งออกมาเป็นกลุ่มตามตัวเลขได้หรือไม่
หากให้นึกภาพตามก็อาจเหมือนการเอาภาพตัวเลขไปให้เด็กคนหนึ่งที่ยังไม่เคยเรียนว่าตัวเลขไหนเขียนยังไงดู แล้วก็ไม่ได้บอกเขาว่าภาพไหนเรียกว่าเป็นเลขอะไร บอกแต่ว่าให้ลองแยกภาพเหล่านี้ออกเป็น 10 กลุ่มโดยดูตามความคล้ายคลึง

ลองเขียนโค้ดสำหรับใช้วิธีการ k เฉลี่ยเพื่อแบ่งกลุ่มดู เสร็จแล้วลองสร้างเมทริกซ์ความสับสนขึ้นมาโดยเทียบกับคำตอบจริงเพื่อดูว่ามีการจัดเลขไหนไปอยู่ในกลุ่มไหนมากที่สุด (รายละเอียดเกี่ยวกับเมทริกซ์ความสับสนดูที่ https://phyblas.hinaboshi.com/20170926)
ลองวาดระบายสีเพื่อให้เห็นชัดขึ้นได้เป็นแบบนี้
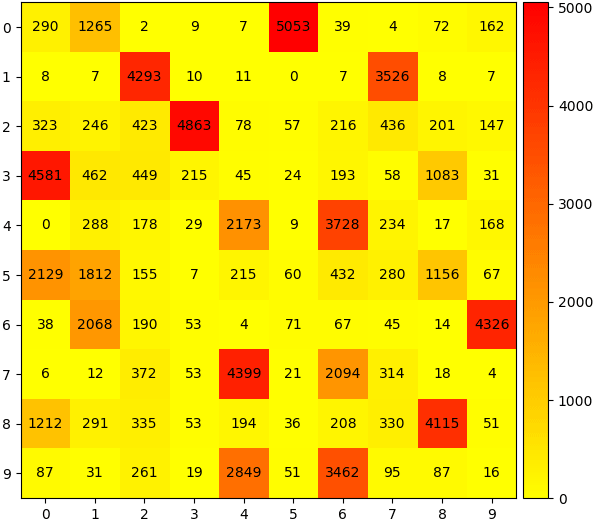
จากตารางนี้ แนวตั้งคือแบ่งคำตอบจริง ซึ่งเรียงตามตัวเลข 0-9 ส่วนแนวนอนคือแบ่งตามกลุ่มที่โปรแกรมแบ่งออกมาให้
แน่นอนว่าเมื่อไม่ได้บอกว่าภาพไหนคือตัวเลขอะไร ทั้ง 10 กลุ่มที่โปรแกรมจะแบ่งออกมาได้ก็จะไม่ได้ติดฉลากว่าเป็นตัวเลขอะไร และจะไม่ได้เรียงตามลำดับด้วย ดังนั้นจึงต้องมาตีความอีกทีว่ากลุ่มที่ได้มาเป็นตัวเลขอะไร
เราจะเห็นได้ว่าแต่ละกลุ่มที่แบ่งได้มีตัวเลขหลายตัวปนอยู่ด้วยกัน แต่ถึงอย่างนั้นก็เห็นได้ว่ามีบางตัวที่อยู่ในกลุ่มนั้นค่อนข้างมากเป็นพิเศษ แสดงให้เห็นว่าการแบ่งไม่ได้สุ่มมั่วแต่อย่างใด ตัวเลขเดียวกันย่อมมีลักษณะบางอย่างที่คล้ายกันจึงถูกจับอยู่กลุ่มเดียวกันได้ง่าย
ลองหาว่าแต่ละกลุ่มมีตัวเลขไหนมากที่สุดได้ดังนี้
จะเห็นว่ากลุ่มที่มีตัวเลข 1 และ 6 นั้นมีอยู่ถึง ๒ กลุ่ม แต่ไม่มีกลุ่มไหนมีเลข 5 และ 9 มากสุดเลย ซึ่งลองดูจากตารางข้างต้นจะเห็นว่าเลข 5 ถูกปนอยู่ในกลุ่มที่เป็นเลข 3 และ 6 ซะมาก ส่วนเลข 9 ปนอยู่กับเลข 4
ผลที่ได้นี้จะต่างกันไปเพราะภายในขั้นตอนของวิธีการ k เฉลี่ยนั้นมีการสุ่มอยู่ในตัว แต่โดยรวมแล้วก็จะไม่ต่างไปจากนี้มาก
จากผลที่ได้เป็นแบบนี้จึงเห็นได้ว่ายากที่จะโปรแกรมจะแบ่งกลุ่มตัวเลขในแบบที่มนุษย์รับรู้ได้เองโดยสมบูรณ์โดยไม่มีการบอกอะไร โดยเฉพาะตัวเลขที่ดูเผินๆแล้วเหมือนจะคล้ายกัน
ลองดูว่าเลข 1 ที่ถูกแบ่งไปยัง ๒ กลุ่มนี้มีความต่างกันยังไง

อย่างนี้นี่เอง กลุ่มแรกตั้งตรง กลุ่มหลังเฉียงๆ ดังนั้นจึงถูกมองว่าเป็นคนละกลุ่มกัน
ลองเทียบเลข 5 กลุ่มที่ถูกจับไปอยู่กับ 3 แล้วก็ที่ถูกไปรวมกับ 6 ดู

ก็จะเห็นว่า 5 ฝั่งซ้ายคล้ายเลข 3 ส่วนฝั่งขวาดูคล้ายเลข 6
การจะให้แยกตัวเลขทั้ง ๑๐ เป็น ๑๐ กลุ่มพอดีนั้นดูจะยากไป ลองเปลี่ยนโจทย์ใหม่เป็นแยกระหว่างเลข 0 กับ 1 ดู โดยคัดเอาเฉพาะภาพที่เป็นเลข 0 กับ 1 จากนั้นใช้ k เฉลี่ยเพื่อแบ่งเป็น ๒ กลุ่ม แล้วก็ลองดูเมทริกซ์ความสับสนอีกที
ได้
ในที่นี้เลข 1 อยู่กลุ่ม 0 แต่เลข 0 อยู่กลุ่ม 1 ถึงจะสลับกันแต่ก็ไม่เกี่ยวเพราะลำดับกลุ่มไม่สำคัญ ที่สำคัญคือจะเห็นได้ว่า ๒ กลุ่มแยกกันชัดเจน
จะเห็นได้ว่าถ้าแค่แบ่ง 0 กับ 1 ออกจากกันละก็ ไม่ต้องมีใครมาบอกว่า 0 กับ 1 ต่างกันยังไง เพราะเป็นเลขที่ต่างกันค่อนข้างชัด
แต่ถ้าลองให้แยกระหว่าง 4 กับ 9 ดู
ได้
ผลที่ได้จะปะปนกัน แสดงแสดงว่า 4 กับ 9 นั้นดูแล้วคล้ายกันมาก ธรรมชาติแยกแยะความต่างของรูปร่างเอาเองได้ยาก
ที่ผ่านมาที่ใช้เป็นเทคนิคการเรียนรู้แบบมีผู้สอน ซึ่งก็คือมีการป้อนข้อมูลภาพตัวเลขพร้อมบอกเฉลยว่าภาพนั้นคือตัวเลขอะไร แบบนี้โปรแกรมก็จะเรียนรู้จากคำตอบที่ให้ไปแล้วหาความแตกต่างในแต่กลุ่ม
แต่คราวนี้จะลองมาใช้เทคนิคการเรียนรู้แบบไม่มีผู้สอนบ้าง นั่นคือจะป้อนแต่ข้อมูลภาพไปโดยไม่บอกว่าภาพนี้เป็นตัวเลขอะไร แล้วให้ลองไปแยกแยะแบ่งภาพเป็นกลุ่มๆเอาเอง
การทำแบบนี้ย่อมยากกว่าแน่นอน เพราะหากให้โปรแกรมแบ่งภาพตัวเลขเอาเองตามธรรมชาติโดยไม่มีมนุษย์ไปกำกับบอกมันจะคิดเองได้หรือว่านี่เป็นเลข 0,1,2,3,... ตามที่เราเข้าใจ
แต่ก็มีค่าพอที่จะลอง น่าสนใจในแง่ที่ว่าธรรมชาติจะสามารถแบ่งแยกแยะตัวเลขที่มนุษย์ใช้ในชีวิตประจำวันจนชินนี้ได้เองหรือเปล่า
วิธีที่จะใช้ในครั้งนี้คือวิธีการ k เฉลี่ย ซึ่งได้อธิบายไปแล้วใน https://phyblas.hinaboshi.com/20171220
โดยจะใช้ sklearn เพื่อความสะดวกในการเขียน https://phyblas.hinaboshi.com/20171224
เราจะลองนำข้อมูลรูปภาพตัวเลขทั้ง 70000 ตัวมาป้อนให้โปรแกรมลองทำการแบ่งกลุ่มดู แล้วดูว่ามันจะแบ่งออกมาเป็นกลุ่มตามตัวเลขได้หรือไม่
หากให้นึกภาพตามก็อาจเหมือนการเอาภาพตัวเลขไปให้เด็กคนหนึ่งที่ยังไม่เคยเรียนว่าตัวเลขไหนเขียนยังไงดู แล้วก็ไม่ได้บอกเขาว่าภาพไหนเรียกว่าเป็นเลขอะไร บอกแต่ว่าให้ลองแยกภาพเหล่านี้ออกเป็น 10 กลุ่มโดยดูตามความคล้ายคลึง

ลองเขียนโค้ดสำหรับใช้วิธีการ k เฉลี่ยเพื่อแบ่งกลุ่มดู เสร็จแล้วลองสร้างเมทริกซ์ความสับสนขึ้นมาโดยเทียบกับคำตอบจริงเพื่อดูว่ามีการจัดเลขไหนไปอยู่ในกลุ่มไหนมากที่สุด (รายละเอียดเกี่ยวกับเมทริกซ์ความสับสนดูที่ https://phyblas.hinaboshi.com/20170926)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import datasets
from sklearn.metrics import confusion_matrix
mnist = datasets.fetch_openml('mnist_784')
X,z = mnist.data,mnist.target
np.random.seed(22)
km = KMeans(10)
km.fit(X)
zk = km.predict(X)
conma = confusion_matrix(z,zk)
print(conma)[[ 290 1265 2 9 7 5053 39 4 72 162]
[ 8 7 4293 10 11 0 7 3526 8 7]
[ 323 246 423 4863 78 57 216 436 201 147]
[4581 462 449 215 45 24 193 58 1083 31]
[ 0 288 178 29 2173 9 3728 234 17 168]
[2129 1812 155 7 215 60 432 280 1156 67]
[ 38 2068 190 53 4 71 67 45 14 4326]
[ 6 12 372 53 4399 21 2094 314 18 4]
[1212 291 335 53 194 36 208 330 4115 51]
[ 87 31 261 19 2849 51 3462 95 87 16]]ลองวาดระบายสีเพื่อให้เห็นชัดขึ้นได้เป็นแบบนี้

จากตารางนี้ แนวตั้งคือแบ่งคำตอบจริง ซึ่งเรียงตามตัวเลข 0-9 ส่วนแนวนอนคือแบ่งตามกลุ่มที่โปรแกรมแบ่งออกมาให้
แน่นอนว่าเมื่อไม่ได้บอกว่าภาพไหนคือตัวเลขอะไร ทั้ง 10 กลุ่มที่โปรแกรมจะแบ่งออกมาได้ก็จะไม่ได้ติดฉลากว่าเป็นตัวเลขอะไร และจะไม่ได้เรียงตามลำดับด้วย ดังนั้นจึงต้องมาตีความอีกทีว่ากลุ่มที่ได้มาเป็นตัวเลขอะไร
เราจะเห็นได้ว่าแต่ละกลุ่มที่แบ่งได้มีตัวเลขหลายตัวปนอยู่ด้วยกัน แต่ถึงอย่างนั้นก็เห็นได้ว่ามีบางตัวที่อยู่ในกลุ่มนั้นค่อนข้างมากเป็นพิเศษ แสดงให้เห็นว่าการแบ่งไม่ได้สุ่มมั่วแต่อย่างใด ตัวเลขเดียวกันย่อมมีลักษณะบางอย่างที่คล้ายกันจึงถูกจับอยู่กลุ่มเดียวกันได้ง่าย
ลองหาว่าแต่ละกลุ่มมีตัวเลขไหนมากที่สุดได้ดังนี้
print(np.argsort(conma,0)[-1])จะเห็นว่ากลุ่มที่มีตัวเลข 1 และ 6 นั้นมีอยู่ถึง ๒ กลุ่ม แต่ไม่มีกลุ่มไหนมีเลข 5 และ 9 มากสุดเลย ซึ่งลองดูจากตารางข้างต้นจะเห็นว่าเลข 5 ถูกปนอยู่ในกลุ่มที่เป็นเลข 3 และ 6 ซะมาก ส่วนเลข 9 ปนอยู่กับเลข 4
ผลที่ได้นี้จะต่างกันไปเพราะภายในขั้นตอนของวิธีการ k เฉลี่ยนั้นมีการสุ่มอยู่ในตัว แต่โดยรวมแล้วก็จะไม่ต่างไปจากนี้มาก
จากผลที่ได้เป็นแบบนี้จึงเห็นได้ว่ายากที่จะโปรแกรมจะแบ่งกลุ่มตัวเลขในแบบที่มนุษย์รับรู้ได้เองโดยสมบูรณ์โดยไม่มีการบอกอะไร โดยเฉพาะตัวเลขที่ดูเผินๆแล้วเหมือนจะคล้ายกัน
ลองดูว่าเลข 1 ที่ถูกแบ่งไปยัง ๒ กลุ่มนี้มีความต่างกันยังไง
plt.figure(figsize=[4,8])
for i in range(8):
plt.subplot(8,2,1+i*2,xticks=[],yticks=[])
plt.imshow(X[(z==1)&(zk==2)][i].reshape(28,28),cmap='binary')
plt.subplot(8,2,2+i*2,xticks=[],yticks=[])
plt.imshow(X[(z==1)&(zk==7)][i].reshape(28,28),cmap='binary')
plt.show()
อย่างนี้นี่เอง กลุ่มแรกตั้งตรง กลุ่มหลังเฉียงๆ ดังนั้นจึงถูกมองว่าเป็นคนละกลุ่มกัน
ลองเทียบเลข 5 กลุ่มที่ถูกจับไปอยู่กับ 3 แล้วก็ที่ถูกไปรวมกับ 6 ดู
plt.figure(figsize=[4,8])
for i in range(8):
plt.subplot(8,4,1+i*4,xticks=[],yticks=[])
plt.imshow(X[(z==5)&(zk==0)][i].reshape(28,28),cmap='Reds')
plt.subplot(8,4,2+i*4,xticks=[],yticks=[])
plt.imshow(X[(z==3)&(zk==0)][i].reshape(28,28),cmap='Reds')
plt.subplot(8,4,3+i*4,xticks=[],yticks=[])
plt.imshow(X[(z==5)&(zk==1)][i].reshape(28,28),cmap='Greens')
plt.subplot(8,4,4+i*4,xticks=[],yticks=[])
plt.imshow(X[(z==6)&(zk==1)][i].reshape(28,28),cmap='Greens')
plt.show()
ก็จะเห็นว่า 5 ฝั่งซ้ายคล้ายเลข 3 ส่วนฝั่งขวาดูคล้ายเลข 6
การจะให้แยกตัวเลขทั้ง ๑๐ เป็น ๑๐ กลุ่มพอดีนั้นดูจะยากไป ลองเปลี่ยนโจทย์ใหม่เป็นแยกระหว่างเลข 0 กับ 1 ดู โดยคัดเอาเฉพาะภาพที่เป็นเลข 0 กับ 1 จากนั้นใช้ k เฉลี่ยเพื่อแบ่งเป็น ๒ กลุ่ม แล้วก็ลองดูเมทริกซ์ความสับสนอีกที
X01 = X[z<2]
z01 = z[z<2]
np.random.seed(23)
km = KMeans(2)
km.fit(X01)
zk01 = km.predict(X01)
print(confusion_matrix(z01,zk01))ได้
[[ 126 6777]
[7871 6]]ในที่นี้เลข 1 อยู่กลุ่ม 0 แต่เลข 0 อยู่กลุ่ม 1 ถึงจะสลับกันแต่ก็ไม่เกี่ยวเพราะลำดับกลุ่มไม่สำคัญ ที่สำคัญคือจะเห็นได้ว่า ๒ กลุ่มแยกกันชัดเจน
จะเห็นได้ว่าถ้าแค่แบ่ง 0 กับ 1 ออกจากกันละก็ ไม่ต้องมีใครมาบอกว่า 0 กับ 1 ต่างกันยังไง เพราะเป็นเลขที่ต่างกันค่อนข้างชัด
แต่ถ้าลองให้แยกระหว่าง 4 กับ 9 ดู
_49 = (z==4)|(z==9)
X49 = X[_49]
z49 = (z[_49]==4).astype(int)
np.random.seed(24)
km = KMeans(2)
km.fit(X49)
zk49 = km.predict(X49)
print(confusion_matrix(z49,zk49))ได้
[[4003 2955]
[3569 3255]]ผลที่ได้จะปะปนกัน แสดงแสดงว่า 4 กับ 9 นั้นดูแล้วคล้ายกันมาก ธรรมชาติแยกแยะความต่างของรูปร่างเอาเองได้ยาก
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib