วิธีการ k เฉลี่ยโดยใช้ sklearn
เขียนเมื่อ 2017/12/24 15:46
แก้ไขล่าสุด 2024/10/12 09:31
ตอนที่แล้วได้แนะนำวิธีการเขียนโปรแกรมเพื่อแบ่งกระจุกข้อมูลด้วยวิธีการ k เฉลี่ยไปแล้วใน https://phyblas.hinaboshi.com/20171220
คำสั่งสำหรับวิธีการ k เฉลี่ยนั้นที่จริงแล้วมีบรรจุอยู่ใน sklearn ซึ่งทำให้สามารถใช้งานได้อย่างง่ายดายสะดวก ดังนั้นในตอนนี้จะมาแนะนำวิธีการใช้
คลาสในลักษณะนี้กับคลาส Kmeans ที่เขียนในตอนที่แล้วมีอยู่ในมอดูลย่อย sklearn.cluster
ตัวอย่างการใช้เบื้องต้น
ขอยกตัวอย่างการใช้โดยสร้างข้อมูลเป็นกระจุกด้วยฟังก์ชัน make_blobs (https://phyblas.hinaboshi.com/20161127) แล้วแบ่งเป็น ๑๐ กลุ่มด้วยวิธี k เฉลี่ย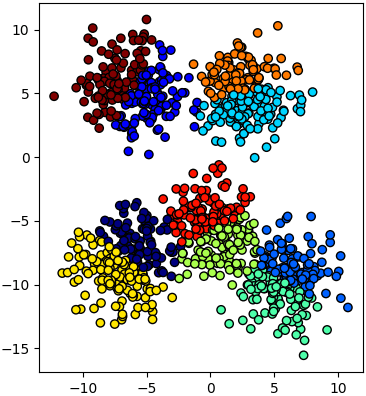
ขั้นตอนการใช้โดยทั่วไปจะเป็นดังที่เห็นคือ
1. สร้างออบเจ็กต์แบบจำลองขึ้นจากคลาส KMeans
2. ใช้เมธอด fit เพื่อป้อนค่าตัวแปรต้นไปให้แบบจำลองทำการเรียนรู้
3. ใช้เมธอด predict เพื่อหาคำตอบว่าแบ่งกลุ่มได้เป็นกลุ่มไหน
หากเทียบกับวิธีการเรียนรู้แบบมีผู้สอนอย่างวิธีการเพื่อนบ้านใกล้สุด k ตัว (https://phyblas.hinaboshi.com/20171031) ก็จะพบว่าคล้ายกัน แต่ที่ต่างกันชัดเจนก็คือในการเรียนรู้ไม่ต้องป้อนข้อมูลผลลัพธ์ (ในที่นี้คือ z) ป้อนแค่ข้อมูลตัวแปรต้น (X)
นอกจากนี้แล้วเรายังสามารถลัดขั้นตอนได้ด้วย โดยใช้เมธอด fit_predict ซึ่งเป็นการให้เรียนรู้เสร็จแล้วก็ทำนายเอาผลของจุดที่เรียนรู้ออกมาทันที ดังนั้นตรง km.fit(X) และ z = km.predict(X) หากเขียนใหม่จะได้เป็น
ผลที่ได้จะไม่ต่างกัน
การปรับแต่ง
ส่วนคีย์เวิร์ดที่ใส่ไปตอนสร้างออบเจ็กต์นั้นจะเป็นตัวปรับแต่งคุณสมบัติของแบบจำลอง โดยตัวที่สำคัญที่สุดคือ n_clusters คือจำนวนกระจุก ในที่นี้ใส่ n_clusters=10 แต่เนื่องจาก n_cluster เป็นคีย์เวิร์ดตัวแรกจะใส่แค่ 10 เฉยๆเลยก็ได้
สรุปคีย์เวิร์ดตอนสร้างออบเจ็กต์
สำหรับ init นั้นคือวิธีการที่จะกำหนดว่าเซนทรอยด์เริ่มต้นควรอยู่ไหน หากเราไม่ได้ใส่อะไรจุดเริ่มต้นจะถูกกำหนดด้วยวิธีที่เรียกว่า k-means++ นี่เป็นอัลกอริธึมในการหาจุดเริ่มต้นที่ดีที่สุดที่นิยมใช้
แต่หากใส่เป็น init='random' ก็จะเริ่มด้วยการสุ่มตำแหน่ง โดยที่ n_init คือจำนวนครั้งที่จะสุ่มจุดเริ่มต้นเพื่อคำนวณหาค่าที่ดีที่สุด
นอกจากนี้หากต้องการกำหนดจุดเริ่มต้นเองก็สามารถทำได้ด้วย โดยใส่ init เป็นอาเรย์ของค่าตำแหน่งเริ่มต้นที่ต้องการ
ค่าที่ถูกเก็บอยู่ภายในหลังเรียนรู้แล้ว
หลังจากใช้เมธอด fit (หรือ fit_predict) ไปแล้วแบบจำลองจะมีการเก็บค่าบางอย่างไว้ สามารถนำมาใช้ได้
.cluster_centers_ คือตำแหน่งของจุดเซนทรอยด์ที่ได้มา จะมีขนาดเท่ากับ (จำนวนเซนทรอยด์,จำนวนมิติ)
.labels_ ผลการแบ่งกลุ่มของข้อมูลที่ใช้เรียนรู้
.inertia_ คือค่าผลรวมความคลาดเคลื่อนกำลังสอง (SSE) ของการแบ่งกลุ่ม
ลองดูค่าที่ได้จากการเรียนรู้ในตัวอย่างเมื่อครู่
ได้
การใช้เพื่อเป็นตัวแปลงพิกัดเพื่อเพิ่มหรือลดมิติของข้อมูล
วิธีการ k เฉลี่ยยังถูกใช้เพื่อแปลงพิกัดของข้อมูลเป็นค่าระยะห่างจากจุดเซนทรอยด์ได้ด้วย
สามารถทำได้โดยที่หลังจากสั่ง .fit หาค่าจุดเซนทรอยด์จากข้อมูลได้แล้ว ก็ใช้เมธอด .transform เพื่อคำนวณค่าระยะห่างจากจุดเซนทรอยด์แต่ละจุด นำค่าที่ได้มาเป็นค่าในระบบพิกัดใหม่
ยกตัวอย่างเช่นลองดูข้อมูลที่มีการแบ่งเป็น ๓ กระจุกในสองมิติ แล้วลองนำมาแปลงพิกัดใหม่เป็นสามมิติตามจำนวนกระจุก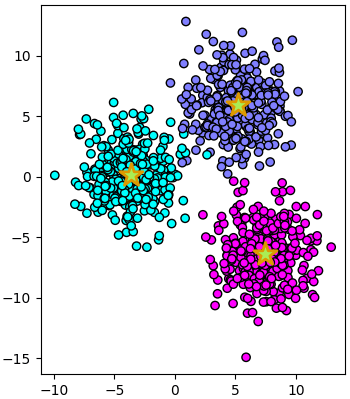
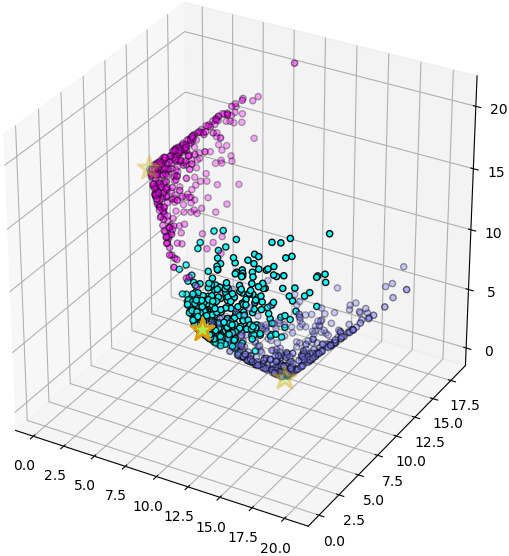
พิกัดใหม่นี้จะมีมิติตามจำนวนเซนทรอยด์ และมีค่าตามระยะห่างจากเซนทรอยด์
สำหรับกรณีที่จะทั้ง fit และ transform จุดเดียวกันไปพร้อมกันแบบนี้สามารถใช้เมธอด .fit_transform เช่นเดียวกับ .fit_predict ดังนั้นอาจเขียนเป็นแบบนี้ได้
ลองสร้างจุดกระจายทั่วในสองมิติแล้วแปลงดู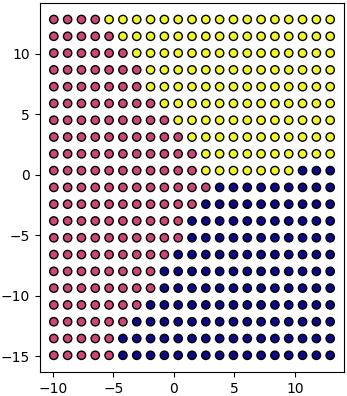
ผลที่ได้เหมือนเอากระดาษสี่เหลี่ยมแผ่นหนึ่งมาแผ่ยืดแผ่ในสามมิติ
นี่เป็นตัวอย่างการแปลงจากมิติน้อยไปมาก แต่จะแปลงจากมิติมากไปน้อยก็ได้เช่นกัน
เช่น ลองแปลงจากข้อมูลที่มี ๘ มิติ ซึ่งไม่สามารถวาดภาพแสดงได้ มาเป็น ๒ มิติ ซึ่งสามารถแสดงแผนภาพการกระจายให้เห็นได้ง่าย
การทำแบบนี้อาจเรียกได้ว่าเป็นวิธีหนึ่งในการลดมิติด้วยการสกัดเอาค่าแทนลักษณะ (特征抽取, feature extraction)
คำสั่งสำหรับวิธีการ k เฉลี่ยนั้นที่จริงแล้วมีบรรจุอยู่ใน sklearn ซึ่งทำให้สามารถใช้งานได้อย่างง่ายดายสะดวก ดังนั้นในตอนนี้จะมาแนะนำวิธีการใช้
คลาสในลักษณะนี้กับคลาส Kmeans ที่เขียนในตอนที่แล้วมีอยู่ในมอดูลย่อย sklearn.cluster
ตัวอย่างการใช้เบื้องต้น
ขอยกตัวอย่างการใช้โดยสร้างข้อมูลเป็นกระจุกด้วยฟังก์ชัน make_blobs (https://phyblas.hinaboshi.com/20161127) แล้วแบ่งเป็น ๑๐ กลุ่มด้วยวิธี k เฉลี่ย
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import datasets
np.random.seed(10)
X,_ = datasets.make_blobs(n_samples=1000,n_features=2,centers=5,cluster_std=2)
km = KMeans(10) # หรือ km = KMeans(n_clusters=10)
km.fit(X)
z = km.predict(X)
plt.axes(aspect=1).scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='jet')
plt.show()
ขั้นตอนการใช้โดยทั่วไปจะเป็นดังที่เห็นคือ
1. สร้างออบเจ็กต์แบบจำลองขึ้นจากคลาส KMeans
2. ใช้เมธอด fit เพื่อป้อนค่าตัวแปรต้นไปให้แบบจำลองทำการเรียนรู้
3. ใช้เมธอด predict เพื่อหาคำตอบว่าแบ่งกลุ่มได้เป็นกลุ่มไหน
หากเทียบกับวิธีการเรียนรู้แบบมีผู้สอนอย่างวิธีการเพื่อนบ้านใกล้สุด k ตัว (https://phyblas.hinaboshi.com/20171031) ก็จะพบว่าคล้ายกัน แต่ที่ต่างกันชัดเจนก็คือในการเรียนรู้ไม่ต้องป้อนข้อมูลผลลัพธ์ (ในที่นี้คือ z) ป้อนแค่ข้อมูลตัวแปรต้น (X)
นอกจากนี้แล้วเรายังสามารถลัดขั้นตอนได้ด้วย โดยใช้เมธอด fit_predict ซึ่งเป็นการให้เรียนรู้เสร็จแล้วก็ทำนายเอาผลของจุดที่เรียนรู้ออกมาทันที ดังนั้นตรง km.fit(X) และ z = km.predict(X) หากเขียนใหม่จะได้เป็น
z = km.fit_predict(X)ผลที่ได้จะไม่ต่างกัน
การปรับแต่ง
ส่วนคีย์เวิร์ดที่ใส่ไปตอนสร้างออบเจ็กต์นั้นจะเป็นตัวปรับแต่งคุณสมบัติของแบบจำลอง โดยตัวที่สำคัญที่สุดคือ n_clusters คือจำนวนกระจุก ในที่นี้ใส่ n_clusters=10 แต่เนื่องจาก n_cluster เป็นคีย์เวิร์ดตัวแรกจะใส่แค่ 10 เฉยๆเลยก็ได้
สรุปคีย์เวิร์ดตอนสร้างออบเจ็กต์
| ความหมาย | ค่าตั้งต้น | |
|---|---|---|
| n_clusters | จำนวนกระจุก | 8 |
| init | ตำแหน่งเริ่มต้นของเซนทรอยด์ | k-means++ |
| n_init | จำนวนครั้งที่เริ่มค้นใหม่โดยตั้งต้นเซนทรอยด์ต่างกัน | 10 |
| max_iter | จำนวนครั้งการปรับจุดเซนทรอย์ดมากสุด | 300 |
| tol | ระยะห่างสูงสุดที่จะถือว่าไม่มีมีการเปลี่ยนแปลง | 1e-4 |
สำหรับ init นั้นคือวิธีการที่จะกำหนดว่าเซนทรอยด์เริ่มต้นควรอยู่ไหน หากเราไม่ได้ใส่อะไรจุดเริ่มต้นจะถูกกำหนดด้วยวิธีที่เรียกว่า k-means++ นี่เป็นอัลกอริธึมในการหาจุดเริ่มต้นที่ดีที่สุดที่นิยมใช้
แต่หากใส่เป็น init='random' ก็จะเริ่มด้วยการสุ่มตำแหน่ง โดยที่ n_init คือจำนวนครั้งที่จะสุ่มจุดเริ่มต้นเพื่อคำนวณหาค่าที่ดีที่สุด
นอกจากนี้หากต้องการกำหนดจุดเริ่มต้นเองก็สามารถทำได้ด้วย โดยใส่ init เป็นอาเรย์ของค่าตำแหน่งเริ่มต้นที่ต้องการ
ค่าที่ถูกเก็บอยู่ภายในหลังเรียนรู้แล้ว
หลังจากใช้เมธอด fit (หรือ fit_predict) ไปแล้วแบบจำลองจะมีการเก็บค่าบางอย่างไว้ สามารถนำมาใช้ได้
.cluster_centers_ คือตำแหน่งของจุดเซนทรอยด์ที่ได้มา จะมีขนาดเท่ากับ (จำนวนเซนทรอยด์,จำนวนมิติ)
.labels_ ผลการแบ่งกลุ่มของข้อมูลที่ใช้เรียนรู้
.inertia_ คือค่าผลรวมความคลาดเคลื่อนกำลังสอง (SSE) ของการแบ่งกลุ่ม
ลองดูค่าที่ได้จากการเรียนรู้ในตัวอย่างเมื่อครู่
print(km.cluster_centers_)
print(km.labels_.shape)
print(km.labels_[:20])
print(km.inertia_)ได้
[[ -5.52548853 -6.49102561]
[ -4.57531022 4.50406492]
[ 6.64139849 -8.36522687]
[ 3.01991442 3.65956666]
[ 5.08543653 -11.02605512]
[ 0.99443006 -7.1657286 ]
[ -7.44528283 -9.38607965]
[ 2.30533539 6.64119426]
[ -0.46264094 -4.12857656]
[ -7.59735744 6.20728313]]
(1000,)
[4 6 9 2 1 8 8 8 4 6 5 4 0 3 6 5 0 6 4 8]
4565.45216688การใช้เพื่อเป็นตัวแปลงพิกัดเพื่อเพิ่มหรือลดมิติของข้อมูล
วิธีการ k เฉลี่ยยังถูกใช้เพื่อแปลงพิกัดของข้อมูลเป็นค่าระยะห่างจากจุดเซนทรอยด์ได้ด้วย
สามารถทำได้โดยที่หลังจากสั่ง .fit หาค่าจุดเซนทรอยด์จากข้อมูลได้แล้ว ก็ใช้เมธอด .transform เพื่อคำนวณค่าระยะห่างจากจุดเซนทรอยด์แต่ละจุด นำค่าที่ได้มาเป็นค่าในระบบพิกัดใหม่
ยกตัวอย่างเช่นลองดูข้อมูลที่มีการแบ่งเป็น ๓ กระจุกในสองมิติ แล้วลองนำมาแปลงพิกัดใหม่เป็นสามมิติตามจำนวนกระจุก
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(26)
X,z = datasets.make_blobs(n_samples=1000,n_features=2,centers=3,cluster_std=2.1)
km = KMeans(n_clusters=3)
km.fit(X)
X2 = km.transform(X)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='cool')
plt.scatter(km.cluster_centers_[:,0],km.cluster_centers_[:,1],300,'#AAEE55',marker='*',edgecolor='#DD9900',lw=2)
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d')
ax.scatter(X2[:,0],X2[:,1],X2[:,2],c=z,edgecolor='k',cmap='cool')
cen = km.transform(km.cluster_centers_)
ax.scatter(cen[:,0],cen[:,1],cen[:,2],s=300,c='#AAEE55',marker='*',edgecolor='#DD9900',lw=2)
plt.show()

พิกัดใหม่นี้จะมีมิติตามจำนวนเซนทรอยด์ และมีค่าตามระยะห่างจากเซนทรอยด์
สำหรับกรณีที่จะทั้ง fit และ transform จุดเดียวกันไปพร้อมกันแบบนี้สามารถใช้เมธอด .fit_transform เช่นเดียวกับ .fit_predict ดังนั้นอาจเขียนเป็นแบบนี้ได้
X2 = km.fit_transform(X)ลองสร้างจุดกระจายทั่วในสองมิติแล้วแปลงดู
mx,my = np.meshgrid(np.linspace(X.min(0)[0],X.max(0)[0],21),np.linspace(X.min(0)[1],X.max(0)[1],21))
mX = np.stack([mx.ravel(),my.ravel()],1)
mz = km.predict(mX)
mX2 = km.transform(mX)
plt.axes(aspect=1)
plt.scatter(mX[:,0],mX[:,1],c=mz,edgecolor='k',cmap='plasma')
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d')
ax.scatter(mX2[:,0],mX2[:,1],mX2[:,2],c=mz,edgecolor='k',cmap='plasma')
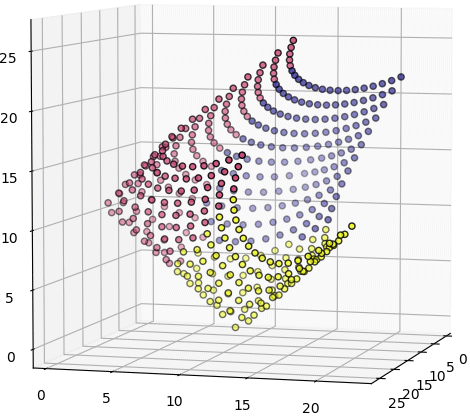
plt.show()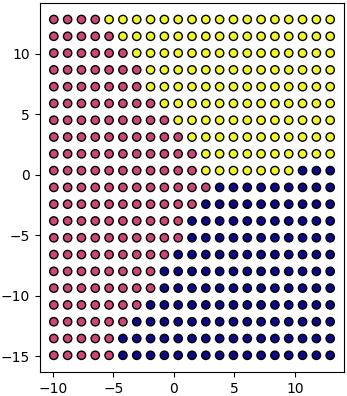

ผลที่ได้เหมือนเอากระดาษสี่เหลี่ยมแผ่นหนึ่งมาแผ่ยืดแผ่ในสามมิติ
นี่เป็นตัวอย่างการแปลงจากมิติน้อยไปมาก แต่จะแปลงจากมิติมากไปน้อยก็ได้เช่นกัน
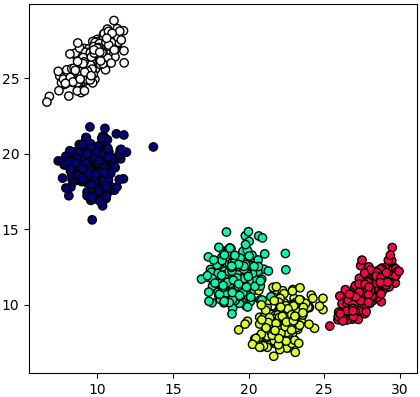
เช่น ลองแปลงจากข้อมูลที่มี ๘ มิติ ซึ่งไม่สามารถวาดภาพแสดงได้ มาเป็น ๒ มิติ ซึ่งสามารถแสดงแผนภาพการกระจายให้เห็นได้ง่าย
np.random.seed(5)
X,z = datasets.make_blobs(n_samples=1000,n_features=8,centers=5,cluster_std=1)
X2 = KMeans(2).fit_transform(X)
plt.figure()
plt.axes(aspect=1)
plt.scatter(X2[:,0],X2[:,1],c=z,edgecolor='k',cmap='gist_ncar')
plt.show()
การทำแบบนี้อาจเรียกได้ว่าเป็นวิธีหนึ่งในการลดมิติด้วยการสกัดเอาค่าแทนลักษณะ (特征抽取, feature extraction)
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn