numpy & matplotlib เบื้องต้น บทที่ ๑๗: การคำนวณและวิเคราะห์ข้อมูลภายในอาเรย์
เขียนเมื่อ 2016/06/11 23:11
แก้ไขล่าสุด 2021/09/28 16:42
ในบทที่ ๓ ได้พูดถึงการนำอาเรย์สองอันขึ้นไปมาทำการคำนวณกันแล้ว แต่ยังไม่ได้พูดถึงการคำนวณและวิเคราะห์ข้อมูลภายในแต่ละอาเรย์
numpy มีฟังก์ชันที่ใช้ในการจัดการข้อมูลภายในอาเรย์อยู่มากมาย ในบทนี้จะแนะนำส่วนหนึ่ง
การหาค่าสูงสุดและต่ำสุด
มีฟังก์ชันที่ใช้หาค่าสูงสุดของสมาชิกในอาเรย์อยู่ ๒ ตัวคือ np.max กับ np.amax ซึ่งความจริงแล้วเป็นฟังก์ชันเดียวกัน เพียงแต่ต่างกันที่ max สามารถเขียนในรูปเมธอดของอาเรย์ได้ นั่นคือ np.max(ar) เท่ากับ ar.max()
ค่าต่ำสุดก็เช่นเดียวกัน มี np.min กับ np.amin
ตัวอย่าง
นอกจากนี้ยังสามารถหาค่าสูงสุดต่ำสุดแยกเป็นแต่ละแกนได้ด้วย โดยเติมคีย์เวิร์ด axis เข้าไป โดยระบุแกนที่จะบวก
กรณีสองมิติจะได้ว่า axis=0 เป็นการคิดตามแนวตั้ง axis=1 เป็นการคิดตามแนวนอน
นอกจากนี้ก็มีฟังก์ชัน np.ptp ซึ่งเอาไว้หาค่าสูงสุดลบค่าต่ำสุด (max-min)
การหาจุดที่มีค่าสูงสุดและต่ำสุด
ฟังก์ชันที่ใช้หาตำแหน่งที่มีค่าสูงสุดคือ np.argmax และต่ำสุดคือ np.argmin มีลักษณะเดียวกับ np.max และ np.min คือเขียนในรูปเมธอดของอาเรย์ได้
ในตัวอย่างนี้ y เป็นฟังก์ชันพาราโบลาร์ หากจะหาว่าจุดต่ำสุดอยู่ที่ x เท่าไหร่ก็ต้องหาดัชนีในอาเรย์ซึ่งให้ค่า y ต่ำสุด ซึ่งทำได้โดยใช้ np.argmin จากนั้นก็เอาตำแหน่งที่ได้มาใช้ใน x ก็จะได้คำตอบเป็น 3
กรณีที่ใช้ในอาเรย์สองมิติขึ้นไปจะเป็นการคืนตำแหน่งที่นับไล่เรียงจากการเอาแต่ละแถวมาต่อกันเป็นหนึ่งมิติ ไม่ใช่คู่อันดับของพิกัด
ตัวอย่าง
แต่หากต้องการจะได้ตำแหน่งพิกัดจำเป็นจะต้องทำการบางอย่างเพิ่มเติม นั่นคือใช้ฟังก์ชัน unravel_index
unravel_index ในที่นี้จะนำค่าดัชนีที่ได้จาก argmax และ argmin ซึ่งเป็นดัชนีในหนึ่งมิติมาแปลงให้เป็นสองมิติ โดยใช้รูปร่างของอาเรย์ ar3.shape เป็นตัวพิจารณาเพื่อไล่ดูว่าหากถูกเปลี่ยนเป็นสองมิติแล้วดัชนีค่านี้จะกลาย เป็นเท่าไหร่
กรณีที่ argmin และ argmax มีการระบุคีย์เวิร์ด axis ไปจะเป็นการบอกตำแหน่งของค่าสูงสุดตามแกน
การหาผลรวม, ค่าเฉลี่ย และมัธยฐาน
ของสมาชิกในอาเรย์หาได้ด้วยฟังก์ชัน np.sum ค่าเฉลี่ยนหาได้จาก np.mean ส่วนมัธยฐานใช้ฟังก์ชัน np.median
sum และ mean สามารถเขียนในรูปเมธอดของอาเรย์ได้ ส่วน median จะต้องเขียนเป็นฟังก์ชันเท่านั้น เขียน ar.median() แบบนี้ไม่ได้
ตัวอย่าง
การใช้ฟังก์ชันเหล่านี้นอกจากจะเขียนง่ายแล้วก็ยังเร็วกว่ามาใช้การวนซ้ำเพื่อคำนวณเองด้วย
ยกตัวอย่างเช่น np.sum ถ้าหากลองสร้างอาเรย์ที่มีสิบล้านตัวแล้วใช้การวนซ้ำบวกสะสมไปทีละตัวตามธรรมดาจะเป็นแบบนี้
ซึ่งจะรู้สึกได้ว่าใช้เวลาไปนานพอสมควร แต่หากใช้ np.sum จะเป็นแบบนี้
จะเห็นว่าเขียนแค่สั้นๆ แถมยังคำนวณเสร็จในพริบตา
ข้อความระวังอย่างหนึ่งก็คือในฟังก์ชันมาตรฐานของไพธอนก็มี sum อยู่แล้ว และก็สามารถใช้กับอาเรย์ได้เช่นกัน เช่น
จะ เห็นว่าต่างจากตัวอย่างที่แล้วแค่ตรงที่ว่าไม่มี .np เท่านั้น แต่ผลที่ได้ก็คือการคำนวณช้ากว่ามาก เพราะ sum นั้นจะคำนวณอาเรย์ในลักษณะเหมือนเป็นลิสต์ จึงไม่ได้ประโยชน์จากความสามารถในการคำนวณเร็วของอาเรย์
ที่น่าสนใจอีกอย่างหนึ่งก็คือ np.sum ก็ใช้กับลิสต์ได้เช่นกัน เช่น
แต่ก็จะเห็นว่ามันทำงานช้า ไม่ต่างจากใช้ sum ธรรมดา
สรุปก็คือ เราจะได้ความเร็วที่เหนือชั้นนี้เมื่อใช้ฟังก์ชันของ numpy ทำงานกับอาเรย์ ดังนั้นหากรู้ว่าจะทำงานกับอาเรย์ก็ให้ใช้ฟังก์ชันของ numpy เป็นหลัก และหลีกเลี่ยงการใช้ for โดยไม่จำเป็น แบบนี้เราก็จะสามารถใช้ numpy ได้อย่างเต็มประสิทธิภาพ
การหาส่วนเบี่ยงเบนมาตรฐานและความแปรปรวน
ส่วนเบี่ยงเบนมาตรฐานหาได้จากฟังก์ชัน np.std ส่วนความแปรปรวนหาได้จากฟังก์ชัน np.var ทั้งสองตัวนี้สามารถเขียนในรูปของเมธอดของอาเรย์ได้
ตัวอย่าง
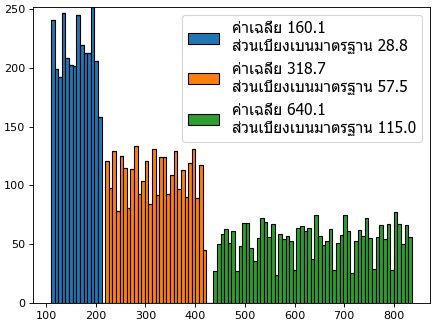
ส่วนเบี่ยงเบนมาตรฐานเป็นสิ่งที่บอกถึงความกระจัดกระจายของข้อมูล ลองวาดฮิสโทแกรมเพื่อเปรียบเทียบดู
ผลรวมสะสมของอาเรย์
บางครั้งเราอาจต้องการหาผลรวมของอาเรย์ที่ไล่จากแถวแรกไปจนถึงแถวหนึ่งๆ ซึ่งสามารถทำได้ด้วยฟังก์ชัน np.cumsum หรือจะเขียนในรูปเมธอดของอาเรย์ก็ได้
ฟังก์ชัน np.cumsum มีไว้หาผลรวมสะสมของอาเรย์ ถ้าไม่ได้กำหนดค่า axis จะได้เป็นอาเรย์หนึ่งมิติ แต่ถ้าระบุ axis จะเป็นการหาผลรวมสะสมตามแนวแกนนั้น
ตัวอย่าง
ลองวาดกราฟเปรียบเทียบระหว่างค่าของตัวอาเรย์กับ cumsum ของอาเรย์
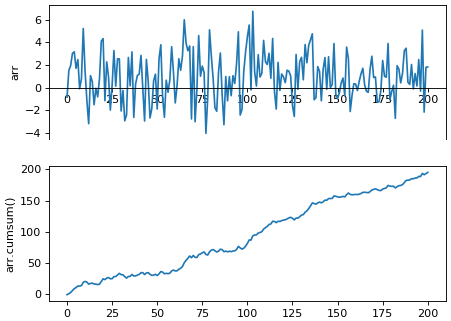
สามารถนำมาใช้ประโยชน์ได้เช่นถ้าต้องการหาตำแหน่งของวัตถุที่เคลื่อนที่อยู่ ก็เอาตำแหน่งที่วัตถุเคลื่อนที่ได้ในแต่ละช่วงมา cumsum ก็จะได้ตำแหน่ง
ลองวาดดู กราฟแสดงตำแหน่งของวัตถุที่มีการเคลื่อนที่แบบสุ่มตามเวลา
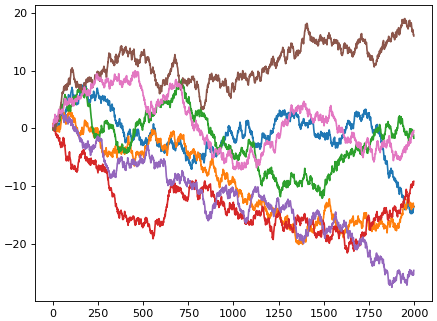
ส่วนอันนี้ดูตำแหน่งการเคลื่อนที่ในสองมิติ
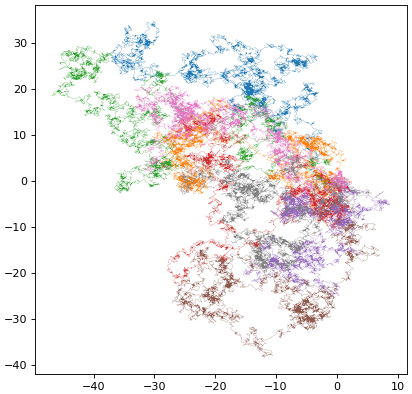
การจัดเรียงค่าภายในอาเรย์
ฟังก์ชันที่ใช้จัดเรียงค่าภายในอาเรย์คือ np.sort โดยจะจัดเรียงตามแกนที่ระบุในคีย์เวิร์ด axis แต่ถ้าไม่ระบุจะจัดเรียงตามแกนสุดท้าย
sort สามารถเขียนในรูปเมธอดของอาเรย์ได้ แต่ความหมายต่างกัน np.sort(ar) เป็นการคืนอาเรย์ที่จัดเรียงแล้วโดยไม่ได้เปลี่ยนแปลงอาเรย์ตัวเก่า แต่ ar.sort() เป็นการจัดเรียงตัวอาเรย์นั้นและไม่มีค่าคืนกลับ
ตัวอย่าง
นอกจากนี้ยังมีฟังก์ชัน argsort ที่เอาไว้หาลำดับของการจัดเรียงค่า
ตัวอย่าง
อ้างอิง
numpy มีฟังก์ชันที่ใช้ในการจัดการข้อมูลภายในอาเรย์อยู่มากมาย ในบทนี้จะแนะนำส่วนหนึ่ง
| np.sum | ผลรวม |
| np.min หรือ np.amin | ค่าต่ำสุด |
| np.max หรือ np.amax | ค่าสูงสุด |
| np.ptp | ค่าสูงสุดลบต่ำสุด |
| np.argmin | ตำแหน่งต่ำสุด |
| np.argmax | ตำแหน่งสูงสุด |
| np.mean | ค่าเฉลี่ยเลขคณิต |
| np.median | มัธยฐาน |
| np.std | ส่วนเบี่ยงเบนมาตรฐาน |
| np.var | ความแปรปรวน |
| np.cumsum | ผลรวมสะสม |
| np.sort | จัดเรียงค่าของสมาชิกในอาเรย์ |
| np.argsort | หาลำดับการจัดเรียงค่าของสมาชิกในอาเรย์ |
การหาค่าสูงสุดและต่ำสุด
มีฟังก์ชันที่ใช้หาค่าสูงสุดของสมาชิกในอาเรย์อยู่ ๒ ตัวคือ np.max กับ np.amax ซึ่งความจริงแล้วเป็นฟังก์ชันเดียวกัน เพียงแต่ต่างกันที่ max สามารถเขียนในรูปเมธอดของอาเรย์ได้ นั่นคือ np.max(ar) เท่ากับ ar.max()
ค่าต่ำสุดก็เช่นเดียวกัน มี np.min กับ np.amin
ตัวอย่าง
import numpy as np
ar1 = np.random.randint(0,100,(4,5))
print(ar1)
# ได้
# [[ 3 55 98 20 62]
# [34 33 12 99 26]
# [90 55 27 82 40]
# [25 21 64 49 57]]
print(np.max(ar1)) # ได้ 99
print(np.min(ar1)) # ได้ 3
ar1 = np.random.randint(0,100,(4,5))
print(ar1)
# ได้
# [[ 3 55 98 20 62]
# [34 33 12 99 26]
# [90 55 27 82 40]
# [25 21 64 49 57]]
print(np.max(ar1)) # ได้ 99
print(np.min(ar1)) # ได้ 3
นอกจากนี้ยังสามารถหาค่าสูงสุดต่ำสุดแยกเป็นแต่ละแกนได้ด้วย โดยเติมคีย์เวิร์ด axis เข้าไป โดยระบุแกนที่จะบวก
กรณีสองมิติจะได้ว่า axis=0 เป็นการคิดตามแนวตั้ง axis=1 เป็นการคิดตามแนวนอน
print(np.min(ar1,axis=0)) # ได้ [ 3 21 12 20 26]
print(np.max(ar1,axis=0)) # ได้ [90 55 98 99 62]
print(np.min(ar1,axis=1)) # ได้ [ 3 12 27 21]
print(np.max(ar1,axis=1)) # ได้ [98 99 90 64]
print(np.max(ar1,axis=0)) # ได้ [90 55 98 99 62]
print(np.min(ar1,axis=1)) # ได้ [ 3 12 27 21]
print(np.max(ar1,axis=1)) # ได้ [98 99 90 64]
นอกจากนี้ก็มีฟังก์ชัน np.ptp ซึ่งเอาไว้หาค่าสูงสุดลบค่าต่ำสุด (max-min)
print(np.ptp(ar1)) # ได้ 96
print(np.ptp(ar1,axis=0)) # ได้ [87 34 86 79 36]
print(np.ptp(ar1,axis=1)) # ได้ [95 87 63 43]
print(np.ptp(ar1,axis=0)) # ได้ [87 34 86 79 36]
print(np.ptp(ar1,axis=1)) # ได้ [95 87 63 43]
การหาจุดที่มีค่าสูงสุดและต่ำสุด
ฟังก์ชันที่ใช้หาตำแหน่งที่มีค่าสูงสุดคือ np.argmax และต่ำสุดคือ np.argmin มีลักษณะเดียวกับ np.max และ np.min คือเขียนในรูปเมธอดของอาเรย์ได้
x = np.arange(0,10,0.2)
y = (x-3)**2+7
print(np.argmin(y)) # ได้ 15
print(x[np.argmin(y)]) # ได้ 3.0
y = (x-3)**2+7
print(np.argmin(y)) # ได้ 15
print(x[np.argmin(y)]) # ได้ 3.0
ในตัวอย่างนี้ y เป็นฟังก์ชันพาราโบลาร์ หากจะหาว่าจุดต่ำสุดอยู่ที่ x เท่าไหร่ก็ต้องหาดัชนีในอาเรย์ซึ่งให้ค่า y ต่ำสุด ซึ่งทำได้โดยใช้ np.argmin จากนั้นก็เอาตำแหน่งที่ได้มาใช้ใน x ก็จะได้คำตอบเป็น 3
กรณีที่ใช้ในอาเรย์สองมิติขึ้นไปจะเป็นการคืนตำแหน่งที่นับไล่เรียงจากการเอาแต่ละแถวมาต่อกันเป็นหนึ่งมิติ ไม่ใช่คู่อันดับของพิกัด
ตัวอย่าง
ar2 = np.random.randint(0,100,(3,5))
print(ar2)
# ได้
# [[72 88 50 36 90]
# [14 46 19 11 12]
# [91 22 21 66 10]]
print(np.argmax(ar2)) # ได้ 10
print(np.argmin(ar2)) # ได้ 14
print(ar2)
# ได้
# [[72 88 50 36 90]
# [14 46 19 11 12]
# [91 22 21 66 10]]
print(np.argmax(ar2)) # ได้ 10
print(np.argmin(ar2)) # ได้ 14
แต่หากต้องการจะได้ตำแหน่งพิกัดจำเป็นจะต้องทำการบางอย่างเพิ่มเติม นั่นคือใช้ฟังก์ชัน unravel_index
ar3 = np.random.randint(0,100,(4,5))
print(ar3)
# ได้
# [[49 65 7 1 85]
# [ 8 66 56 94 7]
# [13 2 33 67 70]
# [97 0 7 19 25]]
print(np.argmax(ar3)) # ได้ 15
print(np.argmin(ar3)) # ได้ 16
print(np.unravel_index(np.argmax(ar3),ar3.shape)) # ได้ (3, 0)
print(np.unravel_index(np.argmin(ar3),ar3.shape)) # ได้ (3, 1)
print(np.unravel_index(15,(4,5))) # ได้ (3, 0)
print(np.unravel_index(16,(4,5))) # ได้ (3, 1)
print(np.unravel_index(14,(4,5))) # ได้ (2, 4)
print(ar3)
# ได้
# [[49 65 7 1 85]
# [ 8 66 56 94 7]
# [13 2 33 67 70]
# [97 0 7 19 25]]
print(np.argmax(ar3)) # ได้ 15
print(np.argmin(ar3)) # ได้ 16
print(np.unravel_index(np.argmax(ar3),ar3.shape)) # ได้ (3, 0)
print(np.unravel_index(np.argmin(ar3),ar3.shape)) # ได้ (3, 1)
print(np.unravel_index(15,(4,5))) # ได้ (3, 0)
print(np.unravel_index(16,(4,5))) # ได้ (3, 1)
print(np.unravel_index(14,(4,5))) # ได้ (2, 4)
unravel_index ในที่นี้จะนำค่าดัชนีที่ได้จาก argmax และ argmin ซึ่งเป็นดัชนีในหนึ่งมิติมาแปลงให้เป็นสองมิติ โดยใช้รูปร่างของอาเรย์ ar3.shape เป็นตัวพิจารณาเพื่อไล่ดูว่าหากถูกเปลี่ยนเป็นสองมิติแล้วดัชนีค่านี้จะกลาย เป็นเท่าไหร่
กรณีที่ argmin และ argmax มีการระบุคีย์เวิร์ด axis ไปจะเป็นการบอกตำแหน่งของค่าสูงสุดตามแกน
ar4 = np.random.randint(0,100,(2,4))
print(ar4)
# ได้
# [[69 93 27 60]
# [61 69 42 85]]
print(np.argmax(ar4,axis=0)) # ได้ [0 0 1 1]
print(np.argmin(ar4,axis=0)) # ได้ [1 1 0 0]
print(np.argmax(ar4,axis=1)) # ได้ [1 3]
print(np.argmin(ar4,axis=1)) # ได้ [2 2]
print(ar4)
# ได้
# [[69 93 27 60]
# [61 69 42 85]]
print(np.argmax(ar4,axis=0)) # ได้ [0 0 1 1]
print(np.argmin(ar4,axis=0)) # ได้ [1 1 0 0]
print(np.argmax(ar4,axis=1)) # ได้ [1 3]
print(np.argmin(ar4,axis=1)) # ได้ [2 2]
การหาผลรวม, ค่าเฉลี่ย และมัธยฐาน
ของสมาชิกในอาเรย์หาได้ด้วยฟังก์ชัน np.sum ค่าเฉลี่ยนหาได้จาก np.mean ส่วนมัธยฐานใช้ฟังก์ชัน np.median
sum และ mean สามารถเขียนในรูปเมธอดของอาเรย์ได้ ส่วน median จะต้องเขียนเป็นฟังก์ชันเท่านั้น เขียน ar.median() แบบนี้ไม่ได้
ตัวอย่าง
ar5 = np.random.randint(0,100,(5,8))
print(ar5)
# ได้
# [[77 14 52 27 77 37 89 58]
# [31 35 25 61 30 78 13 8]
# [16 51 91 69 25 45 67 20]
# [29 99 95 97 13 24 67 68]
# [53 72 59 6 54 31 79 19]]
print(np.sum(ar5)) # ได้ 1961
print(np.mean(ar5)) # ได้ 49.025
print(np.median(ar5)) # ได้ 51.5
print(np.sum(ar5,axis=0)) # ได้ [206 271 322 260 199 215 315 173]
print(np.mean(ar5,axis=0)) # ได้ [ 41.2 54.2 64.4 52. 39.8 43. 63. 34.6]
print(np.median(ar5,axis=0)) # ได้ [ 31. 51. 59. 61. 30. 37. 67. 20.]
print(np.sum(ar5,axis=1)) # ได้ [431 281 384 492 373]
print(np.mean(ar5,axis=1)) # ได้ [ 53.875 35.125 48. 61.5 46.625]
print(np.median(ar5,axis=1)) # ได้ [ 55. 30.5 48. 67.5 53.5]
print(ar5)
# ได้
# [[77 14 52 27 77 37 89 58]
# [31 35 25 61 30 78 13 8]
# [16 51 91 69 25 45 67 20]
# [29 99 95 97 13 24 67 68]
# [53 72 59 6 54 31 79 19]]
print(np.sum(ar5)) # ได้ 1961
print(np.mean(ar5)) # ได้ 49.025
print(np.median(ar5)) # ได้ 51.5
print(np.sum(ar5,axis=0)) # ได้ [206 271 322 260 199 215 315 173]
print(np.mean(ar5,axis=0)) # ได้ [ 41.2 54.2 64.4 52. 39.8 43. 63. 34.6]
print(np.median(ar5,axis=0)) # ได้ [ 31. 51. 59. 61. 30. 37. 67. 20.]
print(np.sum(ar5,axis=1)) # ได้ [431 281 384 492 373]
print(np.mean(ar5,axis=1)) # ได้ [ 53.875 35.125 48. 61.5 46.625]
print(np.median(ar5,axis=1)) # ได้ [ 55. 30.5 48. 67.5 53.5]
การใช้ฟังก์ชันเหล่านี้นอกจากจะเขียนง่ายแล้วก็ยังเร็วกว่ามาใช้การวนซ้ำเพื่อคำนวณเองด้วย
ยกตัวอย่างเช่น np.sum ถ้าหากลองสร้างอาเรย์ที่มีสิบล้านตัวแล้วใช้การวนซ้ำบวกสะสมไปทีละตัวตามธรรมดาจะเป็นแบบนี้
x = np.ones(10000000)
s = 0
for c in x:
s += c
s = 0
for c in x:
s += c
ซึ่งจะรู้สึกได้ว่าใช้เวลาไปนานพอสมควร แต่หากใช้ np.sum จะเป็นแบบนี้
x = np.ones(10000000)
s = np.sum(x)
s = np.sum(x)
จะเห็นว่าเขียนแค่สั้นๆ แถมยังคำนวณเสร็จในพริบตา
ข้อความระวังอย่างหนึ่งก็คือในฟังก์ชันมาตรฐานของไพธอนก็มี sum อยู่แล้ว และก็สามารถใช้กับอาเรย์ได้เช่นกัน เช่น
x = np.ones(10000000)
s = sum(x)
s = sum(x)
จะ เห็นว่าต่างจากตัวอย่างที่แล้วแค่ตรงที่ว่าไม่มี .np เท่านั้น แต่ผลที่ได้ก็คือการคำนวณช้ากว่ามาก เพราะ sum นั้นจะคำนวณอาเรย์ในลักษณะเหมือนเป็นลิสต์ จึงไม่ได้ประโยชน์จากความสามารถในการคำนวณเร็วของอาเรย์
ที่น่าสนใจอีกอย่างหนึ่งก็คือ np.sum ก็ใช้กับลิสต์ได้เช่นกัน เช่น
x = [1]*10000000
s = np.sum(x)
s = np.sum(x)
แต่ก็จะเห็นว่ามันทำงานช้า ไม่ต่างจากใช้ sum ธรรมดา
สรุปก็คือ เราจะได้ความเร็วที่เหนือชั้นนี้เมื่อใช้ฟังก์ชันของ numpy ทำงานกับอาเรย์ ดังนั้นหากรู้ว่าจะทำงานกับอาเรย์ก็ให้ใช้ฟังก์ชันของ numpy เป็นหลัก และหลีกเลี่ยงการใช้ for โดยไม่จำเป็น แบบนี้เราก็จะสามารถใช้ numpy ได้อย่างเต็มประสิทธิภาพ
การหาส่วนเบี่ยงเบนมาตรฐานและความแปรปรวน
ส่วนเบี่ยงเบนมาตรฐานหาได้จากฟังก์ชัน np.std ส่วนความแปรปรวนหาได้จากฟังก์ชัน np.var ทั้งสองตัวนี้สามารถเขียนในรูปของเมธอดของอาเรย์ได้
ตัวอย่าง
ar6 = np.random.randint(0,100,(3,3))
print(ar6)
# ได้
# [[75 35 78]
# [92 84 82]
# [22 75 26]]
print(np.std(ar6)) # ได้ 25.79740632
print(np.var(ar6)) # ได้ 665.50617284
print(np.std(ar6,axis=0)) # ได้ [ 29.81051269 21.29684379 25.50816863]
print(np.var(ar6,axis=0)) # ได้ [ 888.66666667 453.55555556 650.66666667]
print(np.std(ar6,axis=1)) # ได้ [ 19.60158724 4.3204938 24.0970261 ]
print(np.var(ar6,axis=1)) # ได้ [ 384.22222222 18.66666667 580.66666667]
print(np.std(ar6)**2-np.var(ar6)) # ได้ 2.2737367544323206e-13
print(ar6)
# ได้
# [[75 35 78]
# [92 84 82]
# [22 75 26]]
print(np.std(ar6)) # ได้ 25.79740632
print(np.var(ar6)) # ได้ 665.50617284
print(np.std(ar6,axis=0)) # ได้ [ 29.81051269 21.29684379 25.50816863]
print(np.var(ar6,axis=0)) # ได้ [ 888.66666667 453.55555556 650.66666667]
print(np.std(ar6,axis=1)) # ได้ [ 19.60158724 4.3204938 24.0970261 ]
print(np.var(ar6,axis=1)) # ได้ [ 384.22222222 18.66666667 580.66666667]
print(np.std(ar6)**2-np.var(ar6)) # ได้ 2.2737367544323206e-13
ส่วนเบี่ยงเบนมาตรฐานเป็นสิ่งที่บอกถึงความกระจัดกระจายของข้อมูล ลองวาดฮิสโทแกรมเพื่อเปรียบเทียบดู
import numpy as np
import matplotlib.pyplot as plt
ar7 = np.random.randint(110,210,(3000,3)) # สร้างค่าสุ่ม ๓๐๐๐ แถว ๓ หลัก จุดกึ่งกลางอยู่ที่ 160
ar7[:,1] *= 2 # ปรับค่าหลักกลางให้กระจายมากเป็น 2 เท่า จุดกึ่งกลางย้ายไปอยู่ที่ 320
ar7[:,2] *= 4 # ปรับค่าหลักสุดท้ายให้กระจายมากเป็น 4 เท่า จุดกึ่งกลางย้ายไปอยู่ที่ 640
chalia = np.mean(ar7,axis=0) # หาค่าเฉลี่ยแต่ละหลัก
biangben = np.std(ar7,axis=0) # หาส่วนเบี่ยงเบนมาตรฐานแต่ละหลัก
# สร้างลิสต์ที่เก็บข้อความบรรยายกราฟทั้ง ๓
cb = [u'ค่าเฉลี่ย %.1f\nส่วนเบี่ยงเบนมาตรฐาน %.1f'%(c,b) for (c,b) in zip(chalia,biangben)]
# วาดฮิสโทแกรม
plt.hist(ar7,bins=100,stacked=1,label=cb,ec='k')
plt.legend(loc=1,prop={'family':'Tahoma','size':14}) # ใส่คำอธิบาย
plt.show()
import matplotlib.pyplot as plt
ar7 = np.random.randint(110,210,(3000,3)) # สร้างค่าสุ่ม ๓๐๐๐ แถว ๓ หลัก จุดกึ่งกลางอยู่ที่ 160
ar7[:,1] *= 2 # ปรับค่าหลักกลางให้กระจายมากเป็น 2 เท่า จุดกึ่งกลางย้ายไปอยู่ที่ 320
ar7[:,2] *= 4 # ปรับค่าหลักสุดท้ายให้กระจายมากเป็น 4 เท่า จุดกึ่งกลางย้ายไปอยู่ที่ 640
chalia = np.mean(ar7,axis=0) # หาค่าเฉลี่ยแต่ละหลัก
biangben = np.std(ar7,axis=0) # หาส่วนเบี่ยงเบนมาตรฐานแต่ละหลัก
# สร้างลิสต์ที่เก็บข้อความบรรยายกราฟทั้ง ๓
cb = [u'ค่าเฉลี่ย %.1f\nส่วนเบี่ยงเบนมาตรฐาน %.1f'%(c,b) for (c,b) in zip(chalia,biangben)]
# วาดฮิสโทแกรม
plt.hist(ar7,bins=100,stacked=1,label=cb,ec='k')
plt.legend(loc=1,prop={'family':'Tahoma','size':14}) # ใส่คำอธิบาย
plt.show()

ผลรวมสะสมของอาเรย์
บางครั้งเราอาจต้องการหาผลรวมของอาเรย์ที่ไล่จากแถวแรกไปจนถึงแถวหนึ่งๆ ซึ่งสามารถทำได้ด้วยฟังก์ชัน np.cumsum หรือจะเขียนในรูปเมธอดของอาเรย์ก็ได้
ฟังก์ชัน np.cumsum มีไว้หาผลรวมสะสมของอาเรย์ ถ้าไม่ได้กำหนดค่า axis จะได้เป็นอาเรย์หนึ่งมิติ แต่ถ้าระบุ axis จะเป็นการหาผลรวมสะสมตามแนวแกนนั้น
ตัวอย่าง
ar8 = np.random.randint(0,200,(2,5))
print(ar8)
# ได้
# [[ 84 92 25 82 102]
# [190 94 119 36 136]]
print(np.cumsum(ar8)) # ได้ [ 84 176 201 283 385 575 669 788 824 960]
print(np.cumsum(ar8,axis=0))
# ได้
# [[ 84 92 25 82 102]
# [274 186 144 118 238]]
print(np.cumsum(ar8,axis=1))
# ได้
# [[ 84 176 201 283 385]
# [190 284 403 439 575]]
print(ar8)
# ได้
# [[ 84 92 25 82 102]
# [190 94 119 36 136]]
print(np.cumsum(ar8)) # ได้ [ 84 176 201 283 385 575 669 788 824 960]
print(np.cumsum(ar8,axis=0))
# ได้
# [[ 84 92 25 82 102]
# [274 186 144 118 238]]
print(np.cumsum(ar8,axis=1))
# ได้
# [[ 84 176 201 283 385]
# [190 284 403 439 575]]
ลองวาดกราฟเปรียบเทียบระหว่างค่าของตัวอาเรย์กับ cumsum ของอาเรย์
arr = np.random.normal(1,2,201)
ax1 = plt.subplot(2,1,1,ylabel='arr')
ax1.spines['bottom'].set_position(('data',0))
ax1.plot(np.arange(201),arr)
ax2 = plt.subplot(2,1,2,ylabel='arr.cumsum()')
ax2.plot(np.arange(201),arr.cumsum())
plt.show()
ax1 = plt.subplot(2,1,1,ylabel='arr')
ax1.spines['bottom'].set_position(('data',0))
ax1.plot(np.arange(201),arr)
ax2 = plt.subplot(2,1,2,ylabel='arr.cumsum()')
ax2.plot(np.arange(201),arr.cumsum())
plt.show()

สามารถนำมาใช้ประโยชน์ได้เช่นถ้าต้องการหาตำแหน่งของวัตถุที่เคลื่อนที่อยู่ ก็เอาตำแหน่งที่วัตถุเคลื่อนที่ได้ในแต่ละช่วงมา cumsum ก็จะได้ตำแหน่ง
ลองวาดดู กราฟแสดงตำแหน่งของวัตถุที่มีการเคลื่อนที่แบบสุ่มตามเวลา
doen = np.random.rand(7,2000)-0.5
tamnaeng = doen.cumsum(axis=1)
for i in range(7):
plt.plot(np.arange(2000),tamnaeng[i])
plt.show()
tamnaeng = doen.cumsum(axis=1)
for i in range(7):
plt.plot(np.arange(2000),tamnaeng[i])
plt.show()

ส่วนอันนี้ดูตำแหน่งการเคลื่อนที่ในสองมิติ
doen_x = np.random.rand(8,5000)-0.5
doen_y = np.random.rand(8,5000)-0.5
tamnaeng_x = doen_x.cumsum(axis=1)
tamnaeng_y = doen_y.cumsum(axis=1)
plt.figure(figsize=(6,6))
for i in range(8):
plt.plot(tamnaeng_x[i],tamnaeng_y[i],lw=0.2)
plt.show()
doen_y = np.random.rand(8,5000)-0.5
tamnaeng_x = doen_x.cumsum(axis=1)
tamnaeng_y = doen_y.cumsum(axis=1)
plt.figure(figsize=(6,6))
for i in range(8):
plt.plot(tamnaeng_x[i],tamnaeng_y[i],lw=0.2)
plt.show()

การจัดเรียงค่าภายในอาเรย์
ฟังก์ชันที่ใช้จัดเรียงค่าภายในอาเรย์คือ np.sort โดยจะจัดเรียงตามแกนที่ระบุในคีย์เวิร์ด axis แต่ถ้าไม่ระบุจะจัดเรียงตามแกนสุดท้าย
sort สามารถเขียนในรูปเมธอดของอาเรย์ได้ แต่ความหมายต่างกัน np.sort(ar) เป็นการคืนอาเรย์ที่จัดเรียงแล้วโดยไม่ได้เปลี่ยนแปลงอาเรย์ตัวเก่า แต่ ar.sort() เป็นการจัดเรียงตัวอาเรย์นั้นและไม่มีค่าคืนกลับ
ตัวอย่าง
ar9 = np.random.randint(0,100,(4,4))
print(ar9)
# ได้
# [[11 59 84 34]
# [66 59 46 48]
# [87 28 31 97]
# [ 8 27 62 59]]
print(np.sort(ar9))
# ได้
# [[11 34 59 84]
# [46 48 59 66]
# [28 31 87 97]
# [ 8 27 59 62]]
print(np.sort(ar9,axis=0))
# ได้
# [[ 8 27 31 34]
# [11 28 46 48]
# [66 59 62 59]
# [87 59 84 97]]
print(ar9.sort(axis=1)) # ได้ None
print(ar9)
# ได้
# [[11 34 59 84]
# [46 48 59 66]
# [28 31 87 97]
# [ 8 27 59 62]]
print(ar9)
# ได้
# [[11 59 84 34]
# [66 59 46 48]
# [87 28 31 97]
# [ 8 27 62 59]]
print(np.sort(ar9))
# ได้
# [[11 34 59 84]
# [46 48 59 66]
# [28 31 87 97]
# [ 8 27 59 62]]
print(np.sort(ar9,axis=0))
# ได้
# [[ 8 27 31 34]
# [11 28 46 48]
# [66 59 62 59]
# [87 59 84 97]]
print(ar9.sort(axis=1)) # ได้ None
print(ar9)
# ได้
# [[11 34 59 84]
# [46 48 59 66]
# [28 31 87 97]
# [ 8 27 59 62]]
นอกจากนี้ยังมีฟังก์ชัน argsort ที่เอาไว้หาลำดับของการจัดเรียงค่า
ตัวอย่าง
ar10 = np.random.randint(0,100,(3,4))
print(ar10)
# ได้
# [[89 72 55 65]
# [74 35 2 21]
# [31 30 51 87]]
print(np.argsort(ar10))
# ได้
# [[2 3 1 0]
# [2 3 1 0]
# [1 0 2 3]]
print(np.argsort(ar10,axis=0))
# ได้
# [[2 2 1 1]
# [1 1 2 0]
# [0 0 0 2]]
print(ar10.argsort(axis=1))
# ได้
# [[2 3 1 0]
# [2 3 1 0]
# [1 0 2 3]]
print(ar10)
# ได้
# [[89 72 55 65]
# [74 35 2 21]
# [31 30 51 87]]
print(np.argsort(ar10))
# ได้
# [[2 3 1 0]
# [2 3 1 0]
# [1 0 2 3]]
print(np.argsort(ar10,axis=0))
# ได้
# [[2 2 1 1]
# [1 1 2 0]
# [0 0 0 2]]
print(ar10.argsort(axis=1))
# ได้
# [[2 3 1 0]
# [2 3 1 0]
# [1 0 2 3]]
อ้างอิง
http://d.hatena.ne.jp/pashango_p/20090714/1247590272
http://seesaawiki.jp/met-python/d/array
http://rest-term.com/archives/2999
http://www.s12600.net/psy/etc
http://seesaawiki.jp/met-python/d/array
http://rest-term.com/archives/2999
http://www.s12600.net/psy/etc