[python] การวิเคราะห์เส้นโค้งการเรียนรู้เพื่อตรวจดูปัญหาการเรียนรู้เกินหรือเรียนรู้ไม่พอ
เขียนเมื่อ 2017/10/24 20:10
แก้ไขล่าสุด 2022/07/19 06:39
จำนวนของข้อมูลตัวอย่างที่ใช้ในการฝึกมีผลอย่างมากต่อประสิทธิภาพในการฝึกแบบจำลองการเรียนรู้ของเครื่อง
หากลองพิจารณาดูผลการทำนายของแบบจำลองที่ได้ข้อมูลฝึกมามากกับน้อยจะพบว่าความแม่นในการทายผลข้อมูลฝึกกับข้อมูลตรวจสอบนั้นต่างกันไป และแนวโน้มตรงนั้นสามารถบอกให้รู้ว่าควรจะปรับปรุงยังไงต่อได้
เราอาจลองใช้แบบจำลองอันหนึ่งเรียนรู้ข้อมูลที่มีจำนวนแตกต่างกันไปแล้ววาดกราฟระหว่างจำนวนข้อมูลกับคะแนนความแม่นในการทายผลข้อมูลฝึกกับข้อมูลตรวจสอบ
กราฟแบบนั้นเรียกว่าเส้นโค้งการเรียนรู้ (learning curve)
ผลของกราฟที่ได้อาจออกมาดังภาพนี้
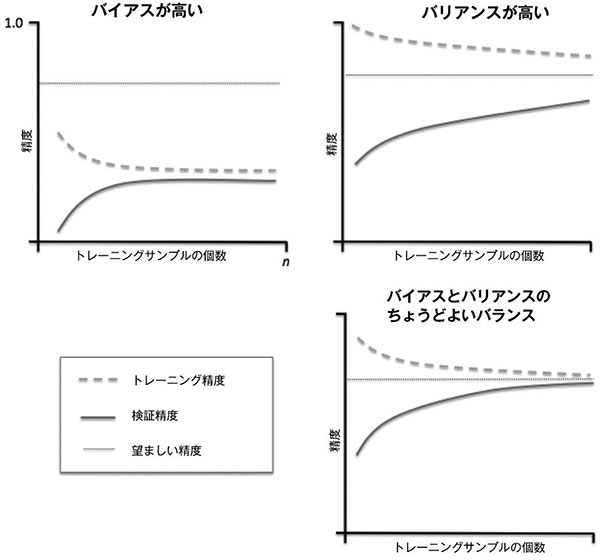
(จากหนังสือ Python機械学習プログラミング 達人データサイエンティストによる理論と実践 https://www.amazon.co.jp/o-ebook/dp/B01HGIPIAK)
--- เส้นประคือความแม่นยำในการทำนายข้อมูลฝึกฝน
ー เส้นทึบคือความแม่นยำในการทำนายข้อมูลตรวจสอบ
ㅡ เส้นตรงบางๆแนวนอนคือค่าค่าความแม่นยำที่น่าพอใจ
ซ้ายบนเป็นแบบจำลองที่มีปัญหาความโน้มเอียง (bias) สูง จะเห็นได้ว่าไม่ว่าข้อมูลฝึกฝนหรือข้อมูลตรงสอบก็ทำนายไม่ได้ผลตามที่น่าพอใจ แบบนี้คือการเรียนรู้ไม่พอ (under-learning) ปัญหาที่พิจารณาอยู่มีความซับซ้อนกว่าที่คิด อาจกำลังวิเคราะห์ปัญหาได้ไม่ตรงจุดเท่าที่ควร
อนึ่ง คำว่า bias ในที่นี้คนละเรื่องกับค่าไบแอสที่เป็นพารามิเตอร์ในแบบจำลองการถดถอยโลจิสติก (รายละเอียด https://phyblas.hinaboshi.com/20161103)
ปัญหาแบบนี้ต่อให่้เพิ่มจำนวนตัวอย่างมากแค่ไหนก็จะไม่ทำให้การเรียนรู้คืบหน้าได้
เพื่อที่จะแก้ปัญหาอาจทำได้โดยเพิ่มจำนวนพารามิเตอร์ที่พิจารณาให้มากขึ้น เพราะบางทีปัจจัยที่พิจารณาอยู่อาจจะไม่มากพอ เช่นสมมุติว่าตรวจเลือดคนไข้ว่ามีสาร a และสาร b อยู่ในเลือดเท่าไหร่เพื่อวิเคราะห์ว่ามีโรคหรือไม่ แต่ไม่ได้พิจารณาสาร c ซึ่งอาจจะมีผลด้วยเช่นกัน
หรืออีกสาเหตุหนึ่งที่เป็นไปได้คือหากแบบจำลองมีการเรกูลาไรซ์อยู่ แล้วเรกูลาไรซ์แรงไป เช่นสำหรับการถดถอยโลจิสติกหรือ SVM ก็คือค่า C ต่ำเกินไป (ดูรายละเอียดได้ใน https://phyblas.hinaboshi.com/20171010) กรณีแบบนี้แก้ได้โดยการปรับค่า C ให้สูงขึ้น
ส่วนภาพขวาบนเกิดปัญหาความแปรปรวน (variance) สูง จะเห็นได้ว่าเมื่อข้อมูลน้อยจะทายผลข้อมูลฝึกได้ดีมาก แต่กลับทายผลข้อมูลตรวจสอบได้ไม่แม่นเลย แบบนี้เรียกว่าการเรียนรู้เกิน (over-learning)
คำว่าความแปรปรวนในที่นี้มีความหมายถึงความเปลี่ยนแปลงที่จะเกิดขึ้นหากมีการเปลี่ยนชุดข้อมูลฝึก
กล่าวคือ หากความแปรปรวนมากจะไวต่อการสุ่ม หมายความว่าพอเปลี่ยนชุดข้อมูลฝึก ผลการทายก็แตกต่างไป
แต่หากความแปรปรวนต่ำต่อให้สุ่มชุดข้อมูลฝึกใหม่กี่ครั้งผลที่ได้ก็จะไม่เปลี่ยนไปมากนัก
จะเห็นว่ายิ่งเพิ่มจำนวนตัวอย่างมากขึ้นผลการทำนายชุดข้อมูลฝึกกับข้อมูลตรวจสอบก็ยิ่งใกล้กัน ดังนั้นปัญหานี้แก้ได้ด้วยการเพิ่มตัวอย่างให้มาก
เพียงแต่ว่าหากข้อมูลได้รับผลจากปัจจัยสุ่มบางอย่างที่ไม่แน่นอนเต็มไปหมด หรือเรียนรู้มากจนอิ่มตัวอยู่แล้ว ต่อให้เพิ่มแค่ไหนก็อาจไม่มีประโยชน์
ขวาล่างคือแบบจำลองที่กำลังดี ความโน้มเอียงไม่สูงไป ความแปรปรวนก็ไม่มากไป ไม่มีทั้งปัญหาการเรียนรู้เกินและเรียนรู้ไม่พอ ได้ผลเป็นที่น่าพอใจ
เพื่อให้เห็นภาพชัดลองดูภาพนี้
หากลองพิจารณาดูผลการทำนายของแบบจำลองที่ได้ข้อมูลฝึกมามากกับน้อยจะพบว่าความแม่นในการทายผลข้อมูลฝึกกับข้อมูลตรวจสอบนั้นต่างกันไป และแนวโน้มตรงนั้นสามารถบอกให้รู้ว่าควรจะปรับปรุงยังไงต่อได้
เราอาจลองใช้แบบจำลองอันหนึ่งเรียนรู้ข้อมูลที่มีจำนวนแตกต่างกันไปแล้ววาดกราฟระหว่างจำนวนข้อมูลกับคะแนนความแม่นในการทายผลข้อมูลฝึกกับข้อมูลตรวจสอบ
กราฟแบบนั้นเรียกว่าเส้นโค้งการเรียนรู้ (learning curve)
ผลของกราฟที่ได้อาจออกมาดังภาพนี้

(จากหนังสือ Python機械学習プログラミング 達人データサイエンティストによる理論と実践 https://www.amazon.co.jp/o-ebook/dp/B01HGIPIAK)
--- เส้นประคือความแม่นยำในการทำนายข้อมูลฝึกฝน
ー เส้นทึบคือความแม่นยำในการทำนายข้อมูลตรวจสอบ
ㅡ เส้นตรงบางๆแนวนอนคือค่าค่าความแม่นยำที่น่าพอใจ
ซ้ายบนเป็นแบบจำลองที่มีปัญหาความโน้มเอียง (bias) สูง จะเห็นได้ว่าไม่ว่าข้อมูลฝึกฝนหรือข้อมูลตรงสอบก็ทำนายไม่ได้ผลตามที่น่าพอใจ แบบนี้คือการเรียนรู้ไม่พอ (under-learning) ปัญหาที่พิจารณาอยู่มีความซับซ้อนกว่าที่คิด อาจกำลังวิเคราะห์ปัญหาได้ไม่ตรงจุดเท่าที่ควร
อนึ่ง คำว่า bias ในที่นี้คนละเรื่องกับค่าไบแอสที่เป็นพารามิเตอร์ในแบบจำลองการถดถอยโลจิสติก (รายละเอียด https://phyblas.hinaboshi.com/20161103)
ปัญหาแบบนี้ต่อให่้เพิ่มจำนวนตัวอย่างมากแค่ไหนก็จะไม่ทำให้การเรียนรู้คืบหน้าได้
เพื่อที่จะแก้ปัญหาอาจทำได้โดยเพิ่มจำนวนพารามิเตอร์ที่พิจารณาให้มากขึ้น เพราะบางทีปัจจัยที่พิจารณาอยู่อาจจะไม่มากพอ เช่นสมมุติว่าตรวจเลือดคนไข้ว่ามีสาร a และสาร b อยู่ในเลือดเท่าไหร่เพื่อวิเคราะห์ว่ามีโรคหรือไม่ แต่ไม่ได้พิจารณาสาร c ซึ่งอาจจะมีผลด้วยเช่นกัน
หรืออีกสาเหตุหนึ่งที่เป็นไปได้คือหากแบบจำลองมีการเรกูลาไรซ์อยู่ แล้วเรกูลาไรซ์แรงไป เช่นสำหรับการถดถอยโลจิสติกหรือ SVM ก็คือค่า C ต่ำเกินไป (ดูรายละเอียดได้ใน https://phyblas.hinaboshi.com/20171010) กรณีแบบนี้แก้ได้โดยการปรับค่า C ให้สูงขึ้น
ส่วนภาพขวาบนเกิดปัญหาความแปรปรวน (variance) สูง จะเห็นได้ว่าเมื่อข้อมูลน้อยจะทายผลข้อมูลฝึกได้ดีมาก แต่กลับทายผลข้อมูลตรวจสอบได้ไม่แม่นเลย แบบนี้เรียกว่าการเรียนรู้เกิน (over-learning)
คำว่าความแปรปรวนในที่นี้มีความหมายถึงความเปลี่ยนแปลงที่จะเกิดขึ้นหากมีการเปลี่ยนชุดข้อมูลฝึก
กล่าวคือ หากความแปรปรวนมากจะไวต่อการสุ่ม หมายความว่าพอเปลี่ยนชุดข้อมูลฝึก ผลการทายก็แตกต่างไป
แต่หากความแปรปรวนต่ำต่อให้สุ่มชุดข้อมูลฝึกใหม่กี่ครั้งผลที่ได้ก็จะไม่เปลี่ยนไปมากนัก
จะเห็นว่ายิ่งเพิ่มจำนวนตัวอย่างมากขึ้นผลการทำนายชุดข้อมูลฝึกกับข้อมูลตรวจสอบก็ยิ่งใกล้กัน ดังนั้นปัญหานี้แก้ได้ด้วยการเพิ่มตัวอย่างให้มาก
เพียงแต่ว่าหากข้อมูลได้รับผลจากปัจจัยสุ่มบางอย่างที่ไม่แน่นอนเต็มไปหมด หรือเรียนรู้มากจนอิ่มตัวอยู่แล้ว ต่อให้เพิ่มแค่ไหนก็อาจไม่มีประโยชน์
ขวาล่างคือแบบจำลองที่กำลังดี ความโน้มเอียงไม่สูงไป ความแปรปรวนก็ไม่มากไป ไม่มีทั้งปัญหาการเรียนรู้เกินและเรียนรู้ไม่พอ ได้ผลเป็นที่น่าพอใจ
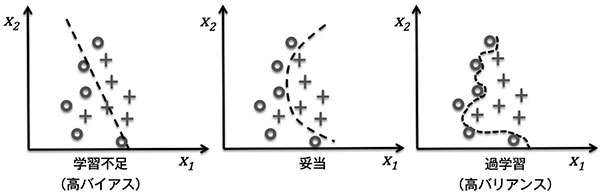
เพื่อให้เห็นภาพชัดลองดูภาพนี้

ทางซ้ายคือเรียนรู้ไม่พอ (ความโน้มเอียงสูง) คือแบบจำลองเรียบง่ายเกิน คิดตื้นเกินไป
ส่วนทางขวาคือเรียนรู้เกิน (ความแปรปรวนสูง) คือแบบจำลองซับซ้อนเกิน คิดลึกเกินไป
ส่วนตรงกลางคือกำลังพอดีๆ ไม่ง่ายและไม่ซับซ้อนเกินไป
ต่อไปมาดูตัวอย่างการวาดเส้นโค้งการเรียนรู้
เราอาจใช้วิธีการตรวจสอบค่าแบบไขว้ k-fold เพื่อทดสอบค่าหลายๆครั้งแล้วเอาคะแนนความแม่นมาเฉลี่ยกัน (รายละเอียด https://phyblas.hinaboshi.com/20171018)
โดยตัวอย่างคราวนี้จะใช้เป็นข้อมูลตัวเลข MNIST (รายละเอียด https://phyblas.hinaboshi.com/20170922)
จะทำการวนคำนวณผลความแม่นของแต่ละรอบซึ่งจำนวนข้อมูลที่ใช้จะต่างกันไป ไล่ตั้งแต่ 500 ไปจนถึง 10000 โดยภายในแต่ละรอบจะมีการใช้ StratifiedKFold เพื่อวนเวียนสลับข้อมูลฝึกและตรวจสอบทั้งหมด ๕ ครั้ง
โค้ดนี้อาจใช้เวลารันนานพอสมควร และวนซ้ำหลายรอบ และรอบหลังๆข้อมูลมากถึงหมื่น
ค่าตัวเลขจำนวนที่ฝึกจะเป็น 0.8 เท่าของจำนวนข้อมูลที่ใช้ในแต่ละรอบ เนื่องจากแบ่ง 1/5 ไปเป็นข้อมูลตรวจสอบทุกครั้ง
ฝึกเสร็จแล้วต่อมาก็วาดกราฟ ขอสร้างเป็นฟังก์ชันไว้สำหรับใช้ตลอดบทความนี้ จากนั้นก็ใช้ดู
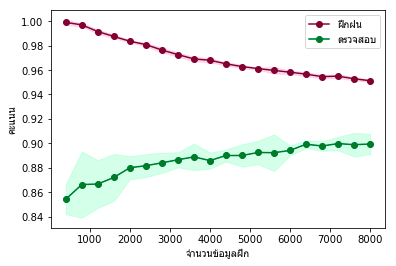
ผลที่ได้จะเห็นได้ว่าผลการทำนายชุดข้อมูลฝึกกับตรวจสอบมีความแตกต่างกันมากโดยเฉพาะเมื่อจำนวนข้อมูลน้อย นั่นคืออยู่ในสภาวะการเรียนรู้เกิน แต่ยิ่งจำนวนข้อมูลมากก็ยิ่งเข้าใกล้กันมากขึ้น
ต่อมาจะแนะนำคำสั่งใน sklearn ที่ช่วยสร้างเส้นโค้งการเรียนรู้โดยง่ายดาย
ที่จริงแล้วขั้นตอนยืดยาวด้านบนทั้งหมดสามารถแทนได้ด้วยการใช้คำสั่ง learning_curve ของ sklearn
คำสั่งนี้จะคล้ายๆกับ validation_curve ที่ได้แนะนำไปแล้วใน https://phyblas.hinaboshi.com/20171020
เพียงแต่ต่างกันตรงที่ validation_curve จะดูผลการเปลี่ยนแปลงไฮเพอร์พารามิเตอร์ ส่วน learning_curve จะดูผลการเปลี่ยนแปลงจำนวนชุดข้อมูลตัวอย่าง
เราอาจเขียนแทนโค้ดข้างต้นได้ดังนี้
train_sizes คือสัดส่วนของจำนวนข้อมูลที่ใช้ในแต่ละครั้งต่อข้อมูลทั้งหมด ในที่นี้กำหนดเป็น np.linspace(0.05,1,20) และข้อมูลมี 10000 หมายความว่ารอบแรกจะมีขนาดเป็น 0.05×10000=500 ต่อมาก็เป็น 0.1×10000=1000 จากนั้นไล่ไปจนถึง 1×10000=10000
ส่วนค่าที่คืนกลับมานั้นจะมีทั้งหมด ๓ ตัว ตัวแรกคืออาเรย์ของจำนวนข้อมูลทดสอบ
ส่วนตัวที่สองและสามคือคะแนนจากการทำนายชุดข้อมูลฝึกและชุดข้อมูลตรวจสอบ ตามลำดับ
ต่อมาลองพิจารณาอีกปัญหาดู สมมุติว่ามีข้อมูลชุดหนึ่งพิจารณาตัวแปร ๓ ตัว สร้างขึ้นมาแล้ววาดดูดังนี้
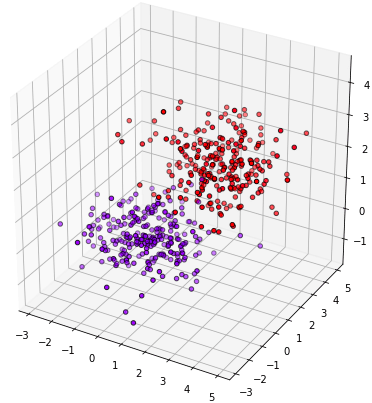
จะเห็นว่าข้อมูลแยกกันเป็น ๒ ส่วนในสามมิติค่อนข้างชัดเจน
แต่ว่าหากลองพิจารณาแค่สองมิติ คือลองลดมิติที่ ๓ ลงไปดู วาดภาพการกระจายในสองมิติโดยละเลยมิติที่สาม
จะเห็นเป็นแบบนี้
จะเห็นว่ามีการซ้อนทับกันอยู่
หากเราลองพิจารณาข้อมูลแค่สองมิติแล้ววิเคราะห์แบ่งกลุ่มโดยใช้การถดถอยโลจิสติก เมื่อลองวาดกราฟการเรียนรู้ออกมา
ก็จะพบว่าผลการเรียนรู้ออกมาแบบนี้
หรือถ้าลองลดมิติลงเหลือแค่หนึ่งแบบนี้
ก็จะยิ่งมีความแม่นยำลดลง
นี่เป็นปัญหาเรื่องความโน้มเอียง เกิดจากการที่แบบจำลองมีความซับซ้อนน้อยเกินไป ในที่นี้คือเกิดจากพิจารณาปัจจัย (ตัวแปร) น้อยกว่าที่ควร
ดังนั้นถ้าพิจารณาโดยใช้ตัวแปรทั้งสามครบหมดดู
ก็จะได้ผลออกมาแม่นขึ้นแบบนี้
บางครั้งการแก้ปัญหาไม่ได้ก็เกิดจากการที่เรามองปัญหาไม่รอบด้านพอนั่นเอง เมื่อเพิ่มมิติของปัญหา มองหาปัจจัยเพิ่มเติมจึงแก้ปัญหาได้
เพียงแต่ในทางตรงกันข้ามก็อาจจะพบว่าเมื่อจำนวนตัวอย่างน้อย มิติสูงจะเกิดปัญหาการเรียนรู้เกินแทน ปัญหานี้อาจเด่นชัดขึ้นเมื่อลองเพิ่มมิติ เช่นลองเพิ่มมิติที่ค่าเป็นการสุ่มล้วน ไม่ได้มีส่วนเกี่ยวข้องกับคำตอบลงไปเลยอีกมิติ
จะพบว่าความแม่นในชุดข้อมูลฝึกฝนเยอะกว่าชุดข้อมูลตรวจสอบมากในขณะที่จำนวนข้อมูลฝึกน้อย นั่นคือมีอาการของการเรียนรู้เกิน เพียงแต่พอมีจำนวนข้อมูลมากปัญหาก็ลดลง
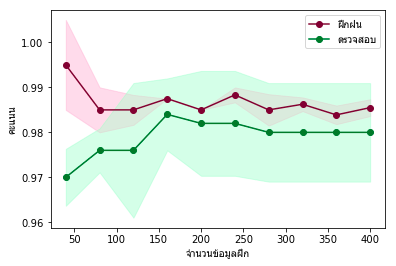
นี่เป็นปัญหาที่เกิดจากการที่คิดปัญหาให้ซับซ้อนเกินจริง ทำเรื่องง่ายให้เป็นเรื่องยาก ไปเอาปัจจัยที่ไม่เกี่ยวข้องมาคิดด้วย ทำให้เกิดการเรียนรู้เกิน
แต่หากตัวอย่างมากพอเราจะรู้ได้ว่าปัจจัยที่ดูเผินๆเหมือนจะมีผลนั้นจริงๆแล้วมันกระจายสุ่มๆ ไม่ได้มีผลอะไรเลย ก็จะเลิกให้ความสำคัญไปเอง อย่างในกราฟนี้ทางฝั่งขวาจะเห็นได้ว่าค่าแทบจะเหมือนกับกรณีคิดแค่สามมิติ นั่นคือผลของมิติที่สี่ที่เกินมาหายไปหมด
กล่าวโดยสรุปแล้ว สิ่งที่เราเรียนรู้ได้จากเรื่องนี้ก็คือ ควรพิจารณาปัญหาให้พอดี ไม่เรียบง่ายหรือซับซ้อนเกินไป
เส้นโค้งการเรียนรู้จะเป็นตัวบอกเราได้ว่าควรปรับปรุงแบบจำลองยังไงให้มองปัญหาได้ในแบบพอดีมากขึ้น
อ้างอิง
ส่วนทางขวาคือเรียนรู้เกิน (ความแปรปรวนสูง) คือแบบจำลองซับซ้อนเกิน คิดลึกเกินไป
ส่วนตรงกลางคือกำลังพอดีๆ ไม่ง่ายและไม่ซับซ้อนเกินไป
ต่อไปมาดูตัวอย่างการวาดเส้นโค้งการเรียนรู้
เราอาจใช้วิธีการตรวจสอบค่าแบบไขว้ k-fold เพื่อทดสอบค่าหลายๆครั้งแล้วเอาคะแนนความแม่นมาเฉลี่ยกัน (รายละเอียด https://phyblas.hinaboshi.com/20171018)
โดยตัวอย่างคราวนี้จะใช้เป็นข้อมูลตัวเลข MNIST (รายละเอียด https://phyblas.hinaboshi.com/20170922)
จะทำการวนคำนวณผลความแม่นของแต่ละรอบซึ่งจำนวนข้อมูลที่ใช้จะต่างกันไป ไล่ตั้งแต่ 500 ไปจนถึง 10000 โดยภายในแต่ละรอบจะมีการใช้ StratifiedKFold เพื่อวนเวียนสลับข้อมูลฝึกและตรวจสอบทั้งหมด ๕ ครั้ง
โค้ดนี้อาจใช้เวลารันนานพอสมควร และวนซ้ำหลายรอบ และรอบหลังๆข้อมูลมากถึงหมื่น
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import StratifiedKFold
from sklearn.linear_model import LogisticRegression as Lori
mnist = datasets.fetch_mldata('MNIST original')
X,z = mnist.data/255.,mnist.target.astype(int)
sumriang = np.random.permutation(70000)
lori = Lori()
khanaen_fuek = []
khanaen_truat = []
nnn = np.linspace(500,10000,20) # ช่วงจำนวนของตัวอย่างที่ใช้ในแต่ละรอบ
chamnuan_fuek = 0.8*nnn # จำนวนตัวอย่างที่ใช้ในการฝึก เป็น 0.8 ของข้อมูลทั้งหมด
for s in nnn:
Xn = X[sumriang[:int(s)]]
zn = z[sumriang[:int(s)]]
skf = StratifiedKFold(n_splits=5,shuffle=True)
k_fuek = []
k_truat = []
for f,t in skf.split(Xn,zn):
X_fuek,z_fuek,X_truat,z_truat = Xn[f],zn[f],Xn[t],zn[t]
lori.fit(X_fuek,z_fuek)
k_fuek.append(lori.score(X_fuek,z_fuek))
k_truat.append(lori.score(X_truat,z_truat))
khanaen_fuek.append(k_fuek)
khanaen_truat.append(k_truat)ค่าตัวเลขจำนวนที่ฝึกจะเป็น 0.8 เท่าของจำนวนข้อมูลที่ใช้ในแต่ละรอบ เนื่องจากแบ่ง 1/5 ไปเป็นข้อมูลตรวจสอบทุกครั้ง
ฝึกเสร็จแล้วต่อมาก็วาดกราฟ ขอสร้างเป็นฟังก์ชันไว้สำหรับใช้ตลอดบทความนี้ จากนั้นก็ใช้ดู
def plottare(c,k1,k2):
plt.figure()
plt.ylabel(u'คะแนน',family='Tahoma')
plt.xlabel(u'จำนวนข้อมูลฝึก',family='Tahoma')
m = np.mean(k1,1)
s = np.std(k1,1)
plt.plot(c,m,'o-',color='#771133')
plt.fill_between(c,m-s,m+s,color='#FFAACC',alpha=0.4)
m = np.mean(k2,1)
s = np.std(k2,1)
plt.plot(c,m,'o-',color='#117733')
plt.fill_between(c,m-s,m+s,color='#AAFFCC',alpha=0.4)
plt.legend([u'ฝึกฝน',u'ตรวจสอบ'],prop={'family':'Tahoma'})
plt.show()
plottare(chamnuan_fuek,khanaen_fuek,khanaen_truat)ผลที่ได้จะเห็นได้ว่าผลการทำนายชุดข้อมูลฝึกกับตรวจสอบมีความแตกต่างกันมากโดยเฉพาะเมื่อจำนวนข้อมูลน้อย นั่นคืออยู่ในสภาวะการเรียนรู้เกิน แต่ยิ่งจำนวนข้อมูลมากก็ยิ่งเข้าใกล้กันมากขึ้น

ต่อมาจะแนะนำคำสั่งใน sklearn ที่ช่วยสร้างเส้นโค้งการเรียนรู้โดยง่ายดาย
ที่จริงแล้วขั้นตอนยืดยาวด้านบนทั้งหมดสามารถแทนได้ด้วยการใช้คำสั่ง learning_curve ของ sklearn
คำสั่งนี้จะคล้ายๆกับ validation_curve ที่ได้แนะนำไปแล้วใน https://phyblas.hinaboshi.com/20171020
เพียงแต่ต่างกันตรงที่ validation_curve จะดูผลการเปลี่ยนแปลงไฮเพอร์พารามิเตอร์ ส่วน learning_curve จะดูผลการเปลี่ยนแปลงจำนวนชุดข้อมูลตัวอย่าง
เราอาจเขียนแทนโค้ดข้างต้นได้ดังนี้
from sklearn.model_selection import learning_curve
mnist = datasets.fetch_mldata('MNIST original')
X,z = mnist.data/255.,mnist.target
sumriang = np.random.permutation(70000)
X,z = X[sumriang[:10000]],z[sumriang[:10000]]
chamnuan_fuek,khanaen_fuek,khanaen_truat = learning_curve(Lori(),X,z,train_sizes=np.linspace(0.1,1,20),cv=5)
plottare(chamnuan_fuek,khanaen_fuek,khanaen_truat) # วาดกราฟด้วยฟังก์ชันอันเดิมที่สร้างไว้ข้างต้นtrain_sizes คือสัดส่วนของจำนวนข้อมูลที่ใช้ในแต่ละครั้งต่อข้อมูลทั้งหมด ในที่นี้กำหนดเป็น np.linspace(0.05,1,20) และข้อมูลมี 10000 หมายความว่ารอบแรกจะมีขนาดเป็น 0.05×10000=500 ต่อมาก็เป็น 0.1×10000=1000 จากนั้นไล่ไปจนถึง 1×10000=10000
ส่วนค่าที่คืนกลับมานั้นจะมีทั้งหมด ๓ ตัว ตัวแรกคืออาเรย์ของจำนวนข้อมูลทดสอบ
ส่วนตัวที่สองและสามคือคะแนนจากการทำนายชุดข้อมูลฝึกและชุดข้อมูลตรวจสอบ ตามลำดับ
ต่อมาลองพิจารณาอีกปัญหาดู สมมุติว่ามีข้อมูลชุดหนึ่งพิจารณาตัวแปร ๓ ตัว สร้างขึ้นมาแล้ววาดดูดังนี้
n = 500
np.random.seed(5)
s = np.random.permutation(n)
X = np.random.normal(0,1.2,[n,3])
X[:,2] /= 2
X[s[int(n/2):]] += 2
z = np.zeros(n)
z[s[int(n/2):]] = 1
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[X.min(),X.max()],ylim=[X.min(),X.max()])
ax.scatter(X[:,0],X[:,1],X[:,2],c=z,edgecolor='k',cmap='rainbow')
plt.show()
จะเห็นว่าข้อมูลแยกกันเป็น ๒ ส่วนในสามมิติค่อนข้างชัดเจน
แต่ว่าหากลองพิจารณาแค่สองมิติ คือลองลดมิติที่ ๓ ลงไปดู วาดภาพการกระจายในสองมิติโดยละเลยมิติที่สาม
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='rainbow')
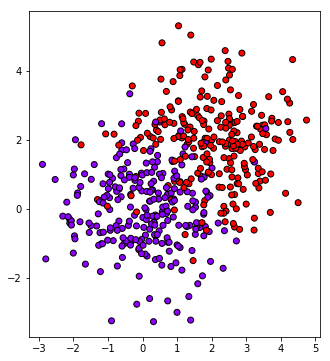
plt.show()จะเห็นเป็นแบบนี้

จะเห็นว่ามีการซ้อนทับกันอยู่
หากเราลองพิจารณาข้อมูลแค่สองมิติแล้ววิเคราะห์แบ่งกลุ่มโดยใช้การถดถอยโลจิสติก เมื่อลองวาดกราฟการเรียนรู้ออกมา
chamnuan_fuek,khanaen_fuek,khanaen_truat = learning_curve(Lori(),X[:,:2],z,train_sizes=np.linspace(0.1,1,10),cv=5)
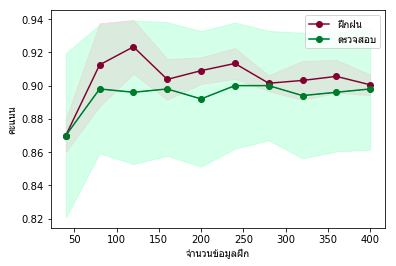
plottare(chamnuan_fuek,khanaen_fuek,khanaen_truat)ก็จะพบว่าผลการเรียนรู้ออกมาแบบนี้

หรือถ้าลองลดมิติลงเหลือแค่หนึ่งแบบนี้
chamnuan_fuek,khanaen_fuek,khanaen_truat = learning_curve(Lori(),X[:,:1],z,train_sizes=np.linspace(0.1,1,10),cv=5)
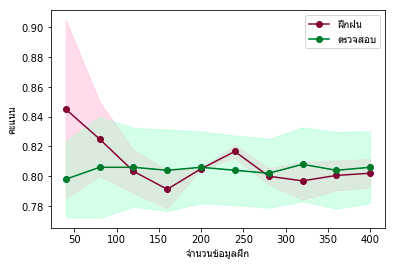
plottare(chamnuan_fuek,khanaen_fuek,khanaen_truat)ก็จะยิ่งมีความแม่นยำลดลง

นี่เป็นปัญหาเรื่องความโน้มเอียง เกิดจากการที่แบบจำลองมีความซับซ้อนน้อยเกินไป ในที่นี้คือเกิดจากพิจารณาปัจจัย (ตัวแปร) น้อยกว่าที่ควร
ดังนั้นถ้าพิจารณาโดยใช้ตัวแปรทั้งสามครบหมดดู
chamnuan_fuek,khanaen_fuek,khanaen_truat = learning_curve(Lori(),X,z,train_sizes=np.linspace(0.1,1,10),cv=5)
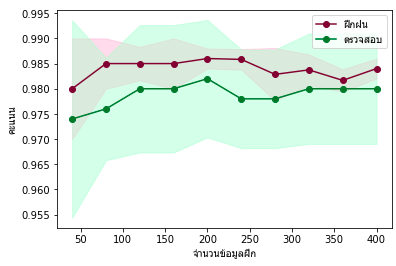
plottare(chamnuan_fuek,khanaen_fuek,khanaen_truat)ก็จะได้ผลออกมาแม่นขึ้นแบบนี้

บางครั้งการแก้ปัญหาไม่ได้ก็เกิดจากการที่เรามองปัญหาไม่รอบด้านพอนั่นเอง เมื่อเพิ่มมิติของปัญหา มองหาปัจจัยเพิ่มเติมจึงแก้ปัญหาได้
เพียงแต่ในทางตรงกันข้ามก็อาจจะพบว่าเมื่อจำนวนตัวอย่างน้อย มิติสูงจะเกิดปัญหาการเรียนรู้เกินแทน ปัญหานี้อาจเด่นชัดขึ้นเมื่อลองเพิ่มมิติ เช่นลองเพิ่มมิติที่ค่าเป็นการสุ่มล้วน ไม่ได้มีส่วนเกี่ยวข้องกับคำตอบลงไปเลยอีกมิติ
X4 = np.hstack([X,np.random.uniform(0,2,[n,1])])
chamnuan_fuek,khanaen_fuek,khanaen_truat = learning_curve(Lori(),X4,z,train_sizes=np.linspace(0.1,1,10),cv=5)
plottare(chamnuan_fuek,khanaen_fuek,khanaen_truat)จะพบว่าความแม่นในชุดข้อมูลฝึกฝนเยอะกว่าชุดข้อมูลตรวจสอบมากในขณะที่จำนวนข้อมูลฝึกน้อย นั่นคือมีอาการของการเรียนรู้เกิน เพียงแต่พอมีจำนวนข้อมูลมากปัญหาก็ลดลง

นี่เป็นปัญหาที่เกิดจากการที่คิดปัญหาให้ซับซ้อนเกินจริง ทำเรื่องง่ายให้เป็นเรื่องยาก ไปเอาปัจจัยที่ไม่เกี่ยวข้องมาคิดด้วย ทำให้เกิดการเรียนรู้เกิน
แต่หากตัวอย่างมากพอเราจะรู้ได้ว่าปัจจัยที่ดูเผินๆเหมือนจะมีผลนั้นจริงๆแล้วมันกระจายสุ่มๆ ไม่ได้มีผลอะไรเลย ก็จะเลิกให้ความสำคัญไปเอง อย่างในกราฟนี้ทางฝั่งขวาจะเห็นได้ว่าค่าแทบจะเหมือนกับกรณีคิดแค่สามมิติ นั่นคือผลของมิติที่สี่ที่เกินมาหายไปหมด
กล่าวโดยสรุปแล้ว สิ่งที่เราเรียนรู้ได้จากเรื่องนี้ก็คือ ควรพิจารณาปัญหาให้พอดี ไม่เรียบง่ายหรือซับซ้อนเกินไป
เส้นโค้งการเรียนรู้จะเป็นตัวบอกเราได้ว่าควรปรับปรุงแบบจำลองยังไงให้มองปัญหาได้ในแบบพอดีมากขึ้น
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn