การแจกแจงความน่าจะเป็นแบบต่างๆ

มอดูลย่อย scipy.stats ใน scipy เป็นมอดูลสำหรับจำลองการแจกแจงความน่าจะเป็นในรูปแบบต่างๆไว้มากมาย

ความสามารถของมอดูลนี้นั้นสามารถทำได้ทั้งสร้างค่าสุ่มตามการแจกแจงความน่าจะเป็นในแบบที่ต้องการ หรือสามารถคำนวณค่าของฟังก์ชันการแจกแจงความน่าจะเป็น หรือความหนาแน่นความน่าจะเป็นสะสมตามที่ต้องการได้

รูปแบบการแจกแจงต่างๆที่ใช้ได้ภายในมอดูลนี้มีเยอะแยะครอบคลุมมากมายจนไม่อาจจะเขียนถึงได้หมด

โดยทั่วไปแบ่งออกเป็น ๓​ กลุ่มหลักๆ คือ

• การแจกแจงแบบไม่ต่อเนื่อง (discrete)
• การแจกแจงแบบต่อเนื่อง (continuous)
• การแจกแจงแบบหลายตัวแปร (multivariate)

โดยรวมแล้วการแจกแจงแบบต่อเนื่องกับการแบบไม่ต่อเนื่องจะมีการใช้งานคล้ายๆกัน มีแค่บางส่วนที่ต่างกัน ซึ่งจะกล่าวถึงต่อไป

ส่วนกลุ่มที่เป็นการแจกแจงแบบหลายตัวแปรนั้นจะค่อนข้างซับซ้อนกว่า ซึ่งต่างกันออกไป ในที่นี้จะไม่เขียนถึงวิธีใช้การแจกแจงกลุ่มนี้ เมธอดต่างๆที่จะแนะนำต่อไปนี้จะเป็นที่ใช้ใน ๒ กลุ่มแรกเป็นหลัก

ในที่นี้จะยกตัวอย่างการแจกแจงต่างๆเฉพาะที่ได้กล่าวถึงไปในบทความความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม ซึ่งมีทั้งหมด ๑๗ แบบ

ก่อนอื่นจะขอเริ่มจากแนะนำชื่อฟังก์ชันใน scipy.stats ที่ใช้สำหรับสร้างการแจกแจงชนิดต่างๆก่อน โดยรายละเอียดของการแจกแจงแต่ละแบบนั้นจะไม่มีการอธิบายในหน้านี้ แต่ดูได้จากลิงก์ที่ตัวเลขทางขวา ซึ่งแสดงบทเนื้อหาที่เกี่ยวข้อง

ชื่อพารามิเตอร์ต่างๆในที่นี้ยึดตามที่เขียนในบทความนั้น แต่ตัวแปรที่แจกแจงจะเขียนเป็น x ทั้งหมด




การแจกแจงแบบไม่ต่อเนื่อง

ชื่อการแจกแจง	ฟังก์ชันมวล (pmf)	x	scipy.stats	พารามิเตอร์	รายละเอียด
การแจกแจงทวินาม	$\begin{align}C(n,x)p^x(1-p)^{n-x}\end{align}$	{0,1,2,...,n}	.binom(n,p)	n ∈ จำนวนเต็มบวก, p ∈ [0,1]	[5], [14]
การแจกแจงแบร์นุลลี	$\begin{align}p^x(1-p)^{1-x}\end{align}$	{0,1}	.bernoulli(p)	p ∈ [0,1]
การแจกแจงทวินามเชิงลบ	$\begin{align}C(x+r-1,x)(1-p)^rp^x\end{align}$	{0,1,2,...}	.nbinom(r,p)	r ∈ จำนวนเต็มบวก, p ∈ [0,1]	[6]
การแจกแจงแบบเรขาคณิต	$\begin{align}p(1-p)^{x-1}\end{align}$	{1,2,...}	.geom(p)	p ∈ [0,1]
การแจกแจงปัวซง	$\begin{align}\frac{λ^x \exp(-λ)}{x!}\end{align}$	{0,1,2,...}	.poisson(λ)	λ ∈ (0,∞)	[7], [10]
การแจกแจงเอกรูปไม่ต่อเนื่อง	$\begin{align}\frac{1}{b-a}\end{align}$	{a,a+1,...,b-1}	.randint(a,b)	a ∈ จำนวนเต็ม, b ∈ จำนวนเต็ม	[4]

โดย C คือจำนวนวิธีการในการจัดหมู่ $\begin{align}C(n,k) = \frac{n!}{k!(n-k)!}\end{align}$




การแจกแจงแบบต่อเนื่อง

ชื่อการแจกแจง	ฟังก์ชันความหนาแน่น (pdf)	x	scipy.stats	พารามิเตอร์	รายละเอียด
การแจกแจงเอกรูปต่อเนื่อง	$\begin{align}\frac{1}{b-a}\end{align}$	[a,b]	.uniform(a,b)	a ∈ (−∞,∞), b ∈ (−∞,∞)	[8]
การแจกแจงแบบปกติ	$\begin{align}\frac{1}{\sqrt{2πσ^2}}\exp\left(-\frac{(x-μ)^2}{2σ^2}\right)\end{align}$	(−∞,∞)	.norm(μ,σ)	μ ∈ (−∞,∞), σ ∈ (0,∞)	[12], [14]
การแจกแจงแบบเลขชี้กำลัง	$\begin{align}λ\exp(-λ(x-μ))\end{align}$	[μ,∞)	.expon(μ,λ)	μ ∈ (-∞,∞) λ ∈ (0,∞)	[10]
การแจกแจงเบตา	$\begin{align}\frac{x^{α-1}(1-x)^{β-1}}{B(α,β)}\end{align}$	(0,1)	.beta(α,β)	α ∈ (0,∞), β ∈ (0,∞)	[11], [15]
การแจกแจงแกมมา	$\begin{align}\frac{β^ν}{Γ(ν)}x^{ν-1}\exp(-βx)\end{align}$ หรือ $\begin{align}\frac{1}{θ^νΓ(ν)}x^{ν-1}\exp\left(-\frac{x}{θ}\right)\end{align}$	(0,∞)	.gamma(ν,1/β) หรือ .gamma(ν,θ)	ν ∈ (0,∞), β ∈ (0,∞)	[16], [19]
การแจกแจงไคกำลังสอง	$\begin{align}\frac{x^{k/2-1}}{\,2^{k/2} \Gamma(k/2)}\exp\left(-\frac{x}{2}\right)\end{align}$	(0,∞)	.chi2(k)	k ∈ จำนวนเต็มบวก	[18]
การแจกแจงสติวเดนต์ที	$\begin{align}\frac{Γ\left(\frac{ν+1}{2}\right)}{\sqrt{νπ}Γ\left(\frac{ν}{2}\right)}\left( 1+\frac{(x-μ)^2}{ν} \right)^{-\frac{ν+1}{2}}\end{align}$	(−∞,∞)	.t(ν)	ω ∈ (0,∞) μ ∈ (-∞,∞)	[20]

โดย

• B คือฟังก์ชันเบตา
• Γ คือฟังก์ชันแกมมา

การแจกแจงแบบหลายตัวแปร

การแจกแจง	ฟังก์ชันความหนาแน่นหรือฟังก์ชันมวล และพารามิเตอร์	รายละเอียด
การแจกแจงแบบปกติหลายตัวแปร .multivariate_normal(μ,Σ)	$\begin{align}\frac{1}{\sqrt{(2π)^m |\mathbf{Σ}|}}\exp{\left(-\frac{1}{2}(\vec{x}-\vec{μ})^T\mathbf{Σ}^{-1}(\vec{x}-\vec{μ})\right)}\end{align}$ $\vec{x} = [x_1,x_2,\cdots,x_m]^T$ $x_iϵ(-∞,∞)$ พารามิเตอร์ $\vec{μ} = [μ_1,μ_2,\cdots,μ_m]^T$, $μ_i ∈ (-∞,∞)$, $\mathbf{Σ} = \begin{bmatrix} σ_{1}^2 & σ_{1,2}^2 & \cdots & σ_{1,m}^2 \\ σ_{2,1}^2 & σ_2^2 & \cdots & σ_{2,m}^2 \\ \vdots & \vdots & \ddots & \vdots \\ σ_{m,1}^2 & σ_m^2 & \cdots & σ_{2,m}^2 \\ \end{bmatrix}$, $σ_i^2 ∈ (0,∞)$, $σ_{i,j}^2 ∈ (-∞,∞)$	[13]
การแจกแจงวิชาร์ต .wishart(ν,V)	$\begin{align}\frac{1}{2^{νm/2} \left|{\mathbf{V}}\right|^{ν/2} Γ_m\left(\frac{ν}{2}\right)}{\left|\mathbf{x}\right|}^{(ν-m-1)/2} \exp\left(-\frac{1}{2}\operatorname{tr}({\mathbf{V}}^{-1}\mathbf{x})\right)\end{align}$ $\mathbf{x} = \begin{bmatrix} x_{1,1}^2 & x_{1,2}^2 & \cdots & x_{1,m}^2 \\ x_{2,1}^2 & x_{2,2}^2 & \cdots & x_{2,m}^2 \\ \vdots & \vdots & \ddots & \vdots \\ x_{m,1}^2 & x_{m,2}^2 & \cdots & x_{m,m}^2 \\ \end{bmatrix}$ $x_{i,j}ϵ(0,∞)$ พารามิเตอร์ $ν ∈ (1,∞)$, $\mathbf{V} = \begin{bmatrix} V_{1,1}^2 & V_{1,2}^2 & \cdots & V_{1,m}^2 \\ V_{2,1}^2 & V_{2,2}^2 & \cdots & V_{2,m}^2 \\ \vdots & \vdots & \ddots & \vdots \\ V_{m,1}^2 & V_{m,2}^2 & \cdots & V_{m,m}^2 \\ \end{bmatrix}$, $V_{i,j} ∈ (0,∞)$	[17]
การแจกแจงอเนกนาม .multinomial(n,p)	$\begin{align}n!\prod_{i=1}^m\frac{p_i^{x_i}}{x_i!}\end{align}$ $\vec{x} = [x_1,x_2,\cdots,x_m]^T$ $x_iϵ\{0,1,...,n\}$ พารามิเตอร์ n ∈ จำนวนเต็ม, $\vec{p}=[p_1,p_2,\cdots,p_m]^T$, $p_i∈[0,1]$	[21]
การแจกแจงดีริคเล .dirichlet(α)	$\begin{align}\frac{1}{B(\vec{α})}\prod_{i=1}^{m}x_i^{α_i-1}\end{align}$ $\vec{x} = [x_1,x_2,\cdots,x_m]^T$ $x_iϵ[0,1]$ พารามิเตอร์ $\vec{α}=[α_1,α_2,\cdots,α_m]^T$, $α_i∈(0,∞)$	[22]

การเริ่มต้นใช้งาน

การใช้งานมอดูลย่อย scipy.stats นั้นจำเป็นต้องสั่ง import scipy.stats โดยตรง จะแค่ import scipy เฉยๆไม่ได้

import scipy
print(scipy.stats) # ได้ AttributeError: module 'scipy' has no attribute 'stats'

สำหรับตัวอย่างต่อๆไปนี้จะ import แบบนี้ทั้งหมด (รวม numpy และ matplotlib ที่ต้องใช้ด้วย)

import scipy.stats
import numpy as np
import matplotlib.pyplot as plt

สร้างค่าสุ่มตามการแจกแจงความน่าจะเป็น

งานหลักของมอดูล scipy.stats ที่มักจะถูกใช้มากที่สุดก็คือการใช้สุ่มค่าเพื่อให้ได้การแจกแจงตามที่ต้องการ

การใช้งานโดยทั่วไปจะเริ่มจากสร้างออบเจ็กต์ตัวแจกแจงขึ้นมา โดยใส่พารามิเตอร์ของการแจกแจงนั้นลงไปตอนนั้น จากนั้นก็เรียกใช้เมธอด .rvs(จำนวน) ก็จะเป็นการสุ่มค่าตามการแจกแจงนั้น

ยกตัวอย่างเช่นลองสุ่มการแจกแจงทวินามสักหมื่นตัว

n = 50
p = 0.05
binom = scipy.stats.binom(n,p)
x = binom.rvs(10000)
plt.hist(x,np.arange(-0.5,x.max()+1),fc='r',ec='k')
plt.show()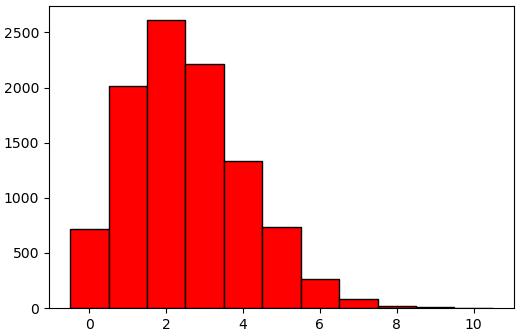

นอกจากนี้ยังมีวิธีลัดในการใช้โดยไม่ต้องสร้างออบเจ็กต์ขึ้นมาก่อน แต่ถ้าต้องการจะทำการสุ่มแค่ครั้งเดียวอยู่แล้วก็อาจจะใช้เมธอด .rvs โดยตรงได้เลย โดยใส่พารามิเตอร์ลงไปเช่นเดียวกับตอนสร้างออบเจ็กต์เฉยๆ ส่วนจำนวนที่ต้องการใส่ให้ใส่เป็นคีย์เวิร์ด size

เช่นสร้างค่า x โดยเขียนแบบนี้ก็ให้ผลเหมือนเดิม

x = scipy.stats.binom.rvs(n,p,size=10000)

การแจกแจงแบบอื่นๆก็ใช้ในลักษณะเดียวกัน แค่เปลี่ยนพารามิเตอร์ เช่นลองดูตัวอย่างการแจกแจงเบตา อาจเขียนได้แบบนี้

α = 3
β = 7
beta = scipy.stats.beta(α,β)
x = beta.rvs(10000)
# หรืออาจเขียนเป็น x = scipy.stats.beta.rvs(α,β,size=10000)
plt.hist(x,50,fc='r',ec='k')
plt.show()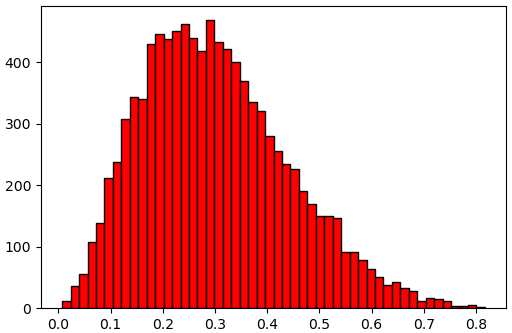

สำหรับการใช้งานตรงส่วนนี้ ทั้งการแจกแจงแบบต่อเนื่องหรือไม่ต่อเนื่องก็มีวิธีการใช้งานเหมือนกัน

การแจกแจงบางส่วนสามารถใช้ np.random ของ numpy แทนได้ เช่นหากต้องการสุ่มการแจกแจงแบบปกติ scipy.stats.norm.rvs() สามารถใช้ np.random.normal()

ส่วนการแจกแจงแบบเอกนามต่อเนื่องก็ใช้ np.random.uniform() ถ้าเป็นเอกนามแบบไม่ต่อเนื่องก็ใช้ np.random.randint()

เกี่ยวกับฟังก์ชันสุ่มต่างๆใน numpy ได้เขียนถึงไว้ใน numpy & matplotlib เบื้องต้น บทที่ ๑๕




คำนวณฟังก์ชันความหนาแน่นของความน่าจะเป็น

สำหรับการแจกแจงแบบต่อเนื่องจะมีเมธอด .pdf() ไว้ใช้คำนวณค่าฟังก์ชันความหนาแน่นของความน่าจะเป็น (probability density function)

ตัวอย่างการใช้งานการแจกแจงทวินาม

α = 2
β = 8
beta = scipy.stats.beta(α,β)
x = np.linspace(0,1,101)
y = beta.pdf(x)
plt.plot(x,y,'r')
plt.show()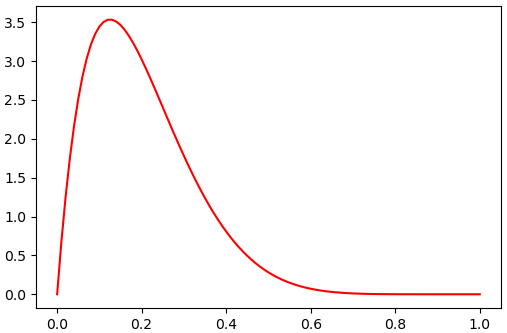

หรืออาจเรียกใช้งานเมธอด .pdf โดยตรงโดยไม่ต้องสร้างขึ้นมาก่อนได้เช่นกัน โดยใส่ค่า x เป็นอาร์กิวเมนต์ตัวแรก แล้วค่อยตามด้วยพารามิเตอร์ตามลำดับ

y = scipy.stats.beta.pdf(x,α,β)

ฟังก์ชันมวลของความน่าจะเป็น

เช่นเดียวกับที่การแจกแจงแบบต่อเนื่องมีเมธอด .pdf() สำหรับการแจกแจงแบบไม่ต่อเนื่องจะมีเมธอด .pmf() ไว้ใช้คำนวณฟังก์ชันมวลของความน่าจะเป็น (probability mass function)

ตัวอย่าง ใช้กับการแจกแจงเบตา

n = 40
p = 0.1
binom = scipy.stats.binom(n,p)
x = np.arange(14)
y = binom.pmf(x)
plt.plot(x,y,'ro-')
plt.show()

สามารถเรียกเมธอด .pmf() โดยตรงได้เช่นกัน

y = scipy.stats.binom.pmf(x,n,p)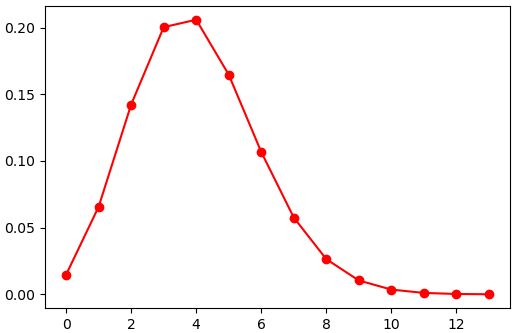

ฟังก์ชันแจกแจงความน่าจะเป็นสะสมหรือฟังก์ชันอยู่รอด

การคำนวณฟังก์ชันแจกแจงสะสม (cumulative distribution function) ทำได้โดยใช้เมธอด .cdf() โดยเมธอดนี้ใช้ได้เหมือนกันทั้งการแจกแจงแบบต่อเนื่องและไม่ต่อเนื่อง

เกี่ยวกับฟังก์ชันแจกแจงสะสมอ่านรายละเอียดได้ใน ความน่าจะเป็นเบื้องต้น บทที่ ๘

ตัวอย่าง ลองใช้กับการแจกแจงทวินาม

n = 20
p = 0.4
binom = scipy.stats.binom(n,p)
x = np.arange(18)
y = binom.cdf(x)
# หรือ y = scipy.stats.binom.cdf(x,n,p)
plt.plot(x,y,'ro-')
plt.show()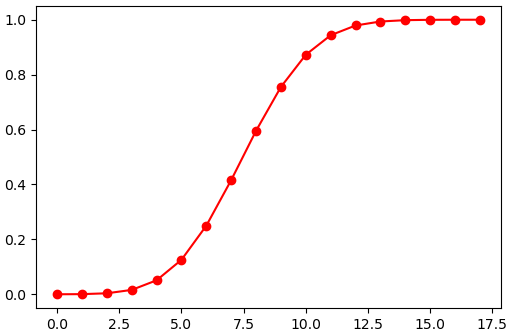

การแจกแจงเบตา

α = 5
β = 4
beta = scipy.stats.beta(α,β)
x = np.linspace(0,1,101)
y = beta.cdf(x)
# หรือ y = scipy.stats.beta.cdf(x,α,β)
plt.plot(x,y,'r')
plt.show()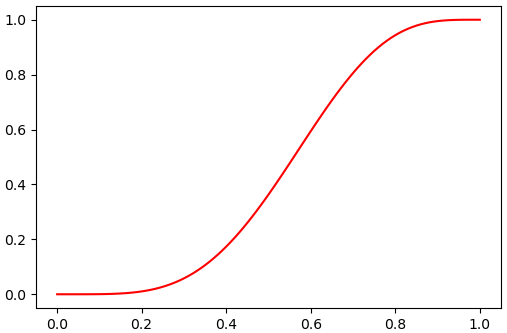

นอกจากนี้มีเมธอด .sf() ซึ่งจะคำนวณค่าฟังก์ชันอยู่รอด (survival function) ซึ่งก็เท่ากับ 1-cdf

y = beta.sf(x)
plt.plot(x,y,'r')
plt.show()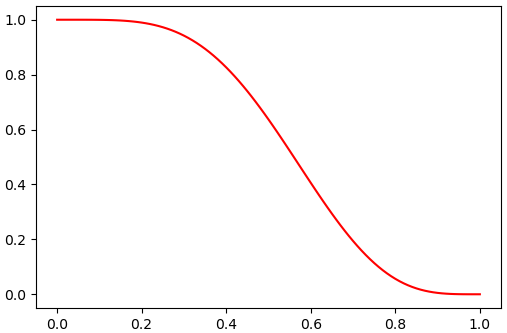

กราฟที่ได้จะกลับกับ .cdf() จากบนลงล่าง




ส่วนกลับของการแจกแจงความน่าจะเป็นสะสม

เมธอด .ppf() ไว้คำนวณค่าส่วนกลับของ cdf ซึ่งเรียกว่าเป็นฟังก์ชันจุดร้อยละ (percent point function) หรือเรียกว่า ฟังก์ชันควอนไทล์ (quantile function)

ค่านี้เป็นค่าที่บอกว่าถ้ามีค่าความน่าจะเป็นรวมถึงเท่านี้แสดงว่าต้องรวมความน่าจะเป็นสะสมมาจนถึงค่าเท่าใด

ตัวอย่าง เมื่อใช้กับการแจกแจงแบบไม่ต่อเนื่องอย่างการแจกแจงทวินาม

n = 10
p = 0.75
binom = scipy.stats.binom(n,p)
q = np.linspace(0,1,1001)
ppf = binom.ppf(q)
plt.plot(q,ppf,'r')
plt.show()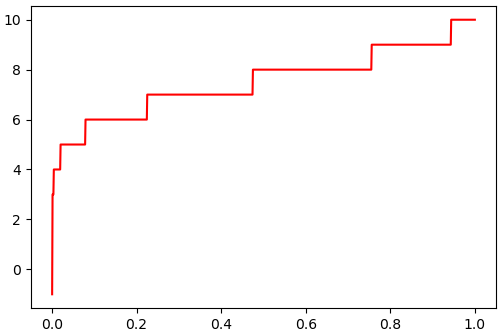

ต่อมาลองใช้กับการแจกแจงแบบต่อเนื่องอย่างการแจกแจงเบตา

α = 10
β = 7
beta = scipy.stats.beta(α,β)
q = np.linspace(0,1,1001)
ppf = beta.ppf(q)
plt.plot(q,ppf,'r')
plt.show()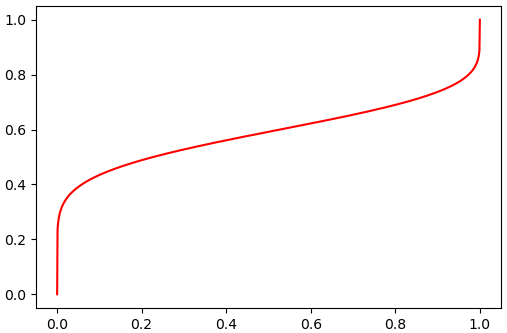

และมีเมธอด .isf ซึ่งเอาไว้คำนวณค่าฟังก์ชันอยู่รอดผกผัน (inverse survival function) ซึ่งก็คือส่วนกลับของ sf กราฟที่ได้จะกลับจาก .ppf() เป็นบนลงล่าง

isf = beta.isf(q)
plt.plot(q,isf,'r')
plt.show()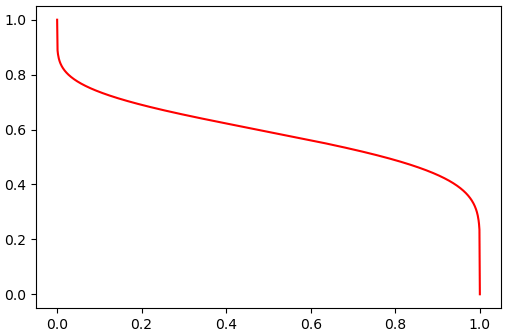

คำนวณค่าคาดหมาย

เมธอด .expect() ใช้คำนวณค่าคาดหมาย (expectation value) จากการแจกแจงนั้นของฟังก์ชันที่ต้องการได้

เกี่ยวกับการคำนวณค่าคาดหมายอ่านรายละเอียดได้ใน ความน่าจะเป็นเบื้องต้น บทที่ ๔

เช่น

n = 10
p = 0.3
binom = scipy.stats.binom(n,p)

def f(x):
    return x**2
print(binom.expect(f)) # ได้ 11.100000000000007

def g(x):
    return 1/(x+1)
print(binom.expect(g)) # ได้ 0.297038403809091

หากไม่ได้ใส่ฟังก์ชันลงไปจะเป็นการหาค่าคาดหมายของ f(x)=x

print(binom.expect()) # ได้ 3.0000000000000013

คำนวณค่าเฉลี่ย, มัธยฐาน, ความแปรปรวน, ส่วนเบี่ยงเบนมาตรฐาน

ค่าต่างๆที่สำคัญทางสถิติ เช่น ค่าเฉลี่ย, มัธยฐาน, ความแปรปรวน, ส่วนเบี่ยงเบนมาตรฐาน ของการแจกแจงแบบต่างๆสามารถคำนวณได้โดยใช้เมธอด .mean() .median() .var() .std()

n = 100
p = 0.2
binom = scipy.stats.binom(n,p)
print(binom.median()) # ได้ 20.0
print(binom.mean()) # ได้ 20.0
print(binom.std()) # ได้ 4.0
print(binom.var()) # ได้ 16.0

α = 3
β = 2
beta = scipy.stats.beta(α,β)
print(scipy.stats.beta.median(α,β)) # ได้ 0.6142724318676104
print(scipy.stats.beta.mean(α,β)) # ได้ 0.6
print(scipy.stats.beta.std(α,β)) # ได้ 0.2
print(scipy.stats.beta.var(α,β)) # 0.04

สรุปเมธอดต่างๆ

ชื่อฟังก์ชัน	ความหมาย
.rvs(size=1, random_state=None)	ทำการสุ่มค่าตามการแจกแจงนั้น
.pmf(x) หรือ .pdf(x)	คำนวณฟังก์ชันมวลหรือฟังก์ชันความหนาแน่น
.logpmf(x) หรือ .logpdf(x)	คำนวณลอการิธึมของฟังก์ชันมวลหรือฟังก์ชันความหนาแน่น
.cdf(x)	คำนวณฟังก์ชันการแจกแจงสะสม
.logcdf(x)	คำนวณลอการิธึมของฟังก์ชันการแจกแจงสะสม
.sf(x)	คำนวณ 1 - cdf
.logsf(x)	คำนวณลอการิธึมของ 1 - cdf
.ppf(q)	คำนวณฟังก์ชันผกผันของ cdf
.isf(q)	คำนวณฟังก์ชันผกผันของ sf
.entropy()	หาเอนโทรปี
.expect(func)	หาค่าคาดหมายของฟังก์ชัน func
.mean()	ค่าเฉลี่ย
.median()	มัธยฐาน
.std()	ส่วนเบี่ยงเบนมาตรฐาน
.var()	ความแปรปรวน

เมธอดที่ขึ้นต้นด้วย .log มีไว้คำนวณค่าลอการิธึมของค่านั้นๆ เช่น .logpdf() .logpmf() ในที่นี้ไม่ได้แสดงตัวอย่างการใช้ให้เห็น แต่วิธีการใช้ก็เหมือนกันกับ .pdf() .pmf() แค่คำนวณออกมาเป็นค่าลอการิธึม

กรณีที่ต้องการคำนวณค่าลอการึธึมให้ใช้เมธอดเหล่านี้โดยตรงจะดีกว่าไปคำนวณลอการิธึมเองภายหลัง เพราะเร็วกว่าและป้องกันตัวเลขสูงหรือต่ำเกิน (overflow & underflow) ได้

ความแตกต่างระหว่างการแจกแจงแบบต่อเนื่องกับไม่ต่อเนื่องที่เห็นชัดที่สุดคือเมธอด .pmf() กับ .pdf() โดยการแจกแจงแบบไม่ต่อเนื่องใช้ .pmf() ส่วนการแจกแจงแบบต่อเนื่องใช้ .pdf()

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -ภูเขาไฟ -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文